运用洛伦兹力分量式的推论巧解物理难题
2010-07-25陈国良
陈国良
(苏州市第一中学校,江苏苏州 215006)
1 推论

图1
我们知道,一带电粒子电荷量为 q,在磁感应强度为B的匀强磁场中做匀速圆周运动,速度大小为 v、方向垂直于磁场方向,则该粒子受到的洛伦兹力的大小 f=qvB、方向垂直于B和v.如图1所示,带电粒子在运动过程中,在y方向上的分速度vy产生x方向的洛伦兹力fx;在x方向上的分速度vx产生y方向的洛伦兹力fy.由此得到洛伦兹力x方向上的分量式为

由牛顿第二定律,有

由(1)、(2)式得

将(3)式积分,得到如下推论

(4)式为匀强磁场中在洛伦兹力作用下做匀速圆周运动的带电粒子在y方向上分运动的表达式.从推导过程可以看出,此推论不仅适用于匀强磁场中做匀速圆周运动的带电粒子,只要带电粒子在 x方向上除受洛伦兹力的作用外,不受其他外力作用或其他外力的合力为零,不管粒子速度大小是否变化、运动路径如何,此推论都成立(实质为质点动量定理的分量式).
同理,在匀强磁场中运动的带电粒子,在 y方向上除受洛伦兹力的作用外,不受其他外力作用或其他外力的合力为零,不管粒子速度大小是否变化、运动路径如何,由洛伦兹力分量式fy=qvxB,可得到其在x方向上分运动的表达式为

2 解题
在磁场中,一些复杂的曲线运动问题求解,如果采用常规方法可能很困难,但如果运用洛伦兹力分量式的推论,可以简单、巧妙地解决.
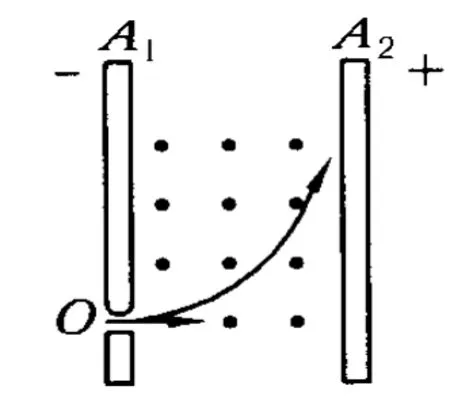
图2
例1.如图2所示,A1和 A2是两块面积很大、互相平行又相距较近的带电金属板,相距为d,两板间的电势差为U.同时,在这两板间还有垂直纸面向外的匀强磁场.一电子(重力不计)由左侧带负电板 A1上的小孔O静止释放,为使该电子不碰到右侧带正电的板 A2,问所加磁场的磁感应强度至少要多大?
解析:电子在电场力作用下开始向右加速运动,同时受到洛伦兹力作用而向上偏转.为使电子不碰到右板 A2,临界条件是当电子到达板 A2时,速度方向刚好与板 A2平行.
电场力水平向右,在竖直方向上电子只受洛伦兹力作用,满足公式(5)的适用条件,有

在电子的运动过程中,电场力做正功,洛伦兹力不做功,由动能定理有

本题电子运动的轨迹既不是抛物线,又不是圆弧,在中学阶段要求解磁感应强度十分困难.若用上述洛伦兹力分量式的推论,可以简单方便地解决问题.
例2.(2008年江苏高考物理题)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O点静止释放,小球的运动曲线如图3所示.已知此曲线在最低点的曲率半径为该点到 x轴距离的2倍,重力加速度为g.求
(1)小球运动到任意位置 P(x,y)的速率 v.
(2)小球在运动过程中第一次下降的最大距离ym.

图3
(2)设在最大距离 ym处的速率为 vm,由圆周运动有


(3)小球运动如图4所示,由动能定理得
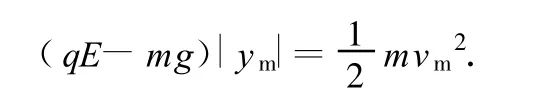

图4
由圆周运动得

且

解得

本题第(2)问可以运用洛伦兹力分量式的推论求解:由于小球在水平方向上除洛伦兹力外不受其他外力作用,满足公式(4)的适用条件,有

由于洛伦兹力不做功,由动能定理得

即

所以

类似地,运用洛伦兹力分量式的推论求解第(3)问:由于带电小球在水平方向只受洛伦兹力作用,满足公式(4)的适用条件,有

小球从O点静止释放后,因洛伦兹力不做功,由动能定理得

由以上两式即可解得

运用洛伦兹力分量式的推论解题,题干中的条件“此曲线在最低点的曲率半径为该点到 x轴距离的2倍”就不必要了,解答更加简洁.
我们还可以将例2题目拓展,运用洛伦兹力分量式的推论来求解第(1)问中的速度方向.


