为何绳端速度如此分解

方银良

(浙江省衢州二中,浙江衢州 324000)

用轻绳相联系的“两体”是高中物理常见的一种理想模型,这一类“两体”问题经常会涉及到“轻绳末端速度”的分解,这是高中物理教学中一个难点.很多资料在介绍速度分解法时,一般就明确告知学生此类问题要按运动的实际效果分解,或沿绳子方向和垂直于绳子方向分解,而没有说明为什么要如此.对此学生知其然而不知其所以然,只能死记,没有真正理解.下面笔者根据自己的教学经验,从例题入手,经发现问题、提出问题、突破难点、例题解析、问题辨析等几个方面一步一步地展开分析讨论,让学生理解为何要把绳端速度如此分解.

例.如图1,甲小车在高台上通过不可伸缩的轻绳拉动地面上的乙小车,甲车以速度 v0做匀速直线运动,当倾斜绳子与水平面夹角为θ时,求乙车的速度v.

分析:乙车的运动是由于绳子的牵引作用,但乙车并不沿绳子收缩方向运动,它沿水平方向运动.设甲车拉绳子速度v0(即沿绳子方向速度)为牵引速度,很明显乙车的速度不等于绳子牵引速度v0.要求乙车速度,一定得从绳子运动入手,那么两者速度到底有什么关系呢?分析绳子上的点,倾斜部分绳子上的各点的运动不沿绳子收缩方向(如B点沿BB′运动,A点沿水平面运动),所以其上各点的速度是不一样的,也不等于绳子牵引速度 v0,但由于绳子的不可伸缩性,倾斜部分绳子上点的速度在绳子上的投影都等于牵引速度v0.设绳子与乙车的接点为 A,则整根绳子上,只有A点的运动才是反映乙车的运动.那么 A点的速度是多少呢?

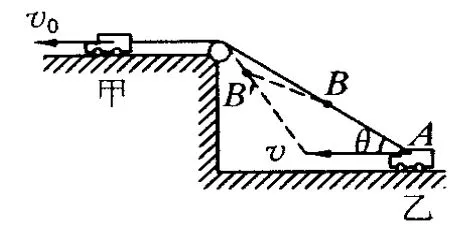
图1

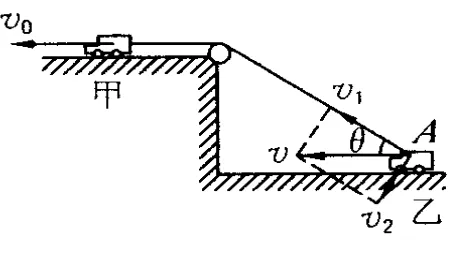
图2

现在我们就来研究接点A的实际运动.A点水平向左运动,可以看成如下两个分运动的合成:一个沿绳子方向v1,一个垂直于绳子方向 v2(如图2).两分运动产生两个效果:v1的作用是使绳子收缩,v2的作用是使绳子转动.因为垂直绳子方向的速度 v2对绳子收缩没影响,故分速度v1与绳子牵引速度相等,即v1=v0,由平行四边形定则可得此时乙物体的速度大小为

对于上面的分析,学生有疑惑:A点运动为何一定要按图2方向分解?沿其他方向分解不行吗?

从理论上讲,一个矢量不论是力、加速度、位移还是速度,都可以分解为无数对大小和方向不同的分矢量,而不像两矢量合成那样具有唯一性.一个实际的运动跟它的分运动形式无关,只要分运动的合成是唯一的合运动.即每一个分运动可能产生的影响可以不同,但所有分运动对物体总的影响是不变的.比如斜抛运动的分解,可以分解为竖直方向的匀变速直线运动和水平方向的匀速直线运动;也可以是竖直方向的匀变速直线运动和初速方向的匀速直线运动;还可以是沿初速方向的匀变速直线运动和垂直初速方向的匀变速直线运动等.

对于上述 A点的运动,也应该有多种分解方式.现在按图3来分解,v3沿绳子方向,v4竖直向下.分析两分速度的影响:因为 v4的作用既使绳子转动,又使绳子伸长,它对绳子的收缩起作用,故分速度v3虽沿绳子方向,作用是使绳子收缩,它的大小却与绳子牵引速度v0不相等.它们具体关系满足v3-v4sinθ=v0,又因为 A点实际是水平运动,故 v3sinθ=v4,而乙物体的速度大小 v=v3◦cosθ,由以上可得结论是一样的.

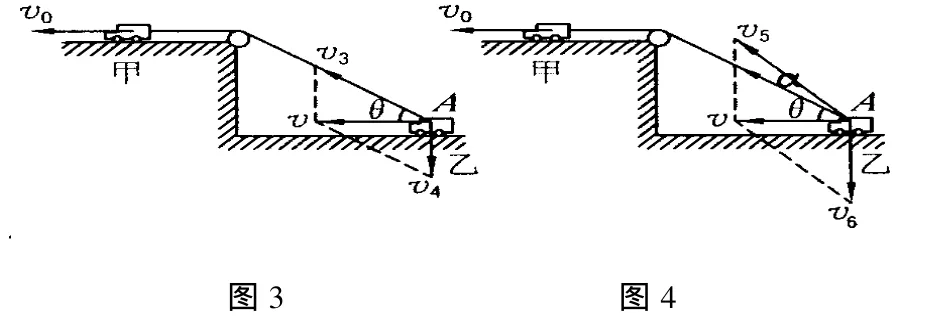
又如按图4分解,v5方向与倾斜绳子的夹角为α,v6竖直向下.这时两个分速度对绳子的收缩和转动都起作用.因为绳子被牵引速度大小是不变的,可得方程 v5cosαv6sinθ=v0;又因为 A点水平运动,故 v5sin(α+θ)=v6,v=v5cos(α+θ).由以上方程可得结论还是一样的.

综上所述,一个合运动的分解方式应该是无数的,只是不同方法的解题难易差别很大.对于理想绳子端速度的分解,主要应理解两点:一是绳子上各点的速度在绳上的投影是一样的;二是弄清绳端的运动实际方向,即合运动的方向.绳端运动的分解可以任意,但要考虑清楚每个分运动产生的影响.如按图2方式分解,两分速度相互垂直,它们所起的影响相互独立,所列方程比较简单.而若按其他方向分解,那么各分速度的作用相互牵扯,列出的方程就比较复杂.所以,绳端速度分解一般沿绳子方向和垂直于绳子方向.

实际上,对于所有矢量的分解都是一样,总是选取对解决问题最方便的分解方式.