中国初婚年龄性别匹配模型及其应用

2010-07-23陈正伟

统计与决策 2010年3期

关键词：婚配婚龄性别比

陈正伟

（重庆工商大学数学与统计学院，重庆 400060）

0 引言

年龄择偶意向是指人们在一定时间和范围内，对婚姻配偶选择的年龄偏好分布的统计规律。一个人进入婚龄后，就会自觉或不自觉的置身于婚姻市场中，被纳入对配偶的供给和需求关系体系，在这个婚姻市场的供求关系中进行比较、选择和匹配，从而体现其择偶意向。

人们对配偶的选择除了受到婚龄期男女人数的多少以及性别平衡等人口学因素的影响外，更受到社会经济文化以及个人的婚姻条件等因素地影响与左右。因此，导致择偶难的原因很多。

本文拟以2005年的重庆市1%人口抽样调查数据和2005年全国1%人口抽样调查数据为依据，从男女已婚人数的多少以及婚龄期性别比等人口学因素的角度，用定量分析方法对中国中青年的初婚年龄择偶倾向及婚姻状况的问题进行探讨。

1 初婚择偶意向分析方法

1.1 数据分析及模型参数

所谓年龄择偶意向是指一定时间、地区范围内，某一年龄组的女性或男性对其他各年龄组的男性或女性的亲合程度或吸引程度。择偶意向的分析，可以帮助我们发现某一年龄组的女性或男性在其他各年龄上的分布规律，以揭示初婚年龄性别比的规律。

设Mi为第i年龄组的男性人数，i表示满了i周岁但不到i+1周岁的年龄组。Wj为第j年龄组的女性人数，j为满了j周岁但不到j+1周岁的年龄组。根据1980年我国婚姻法的规定男性始婚龄为22岁以上，女性始婚龄为20岁以上，故有i≥22，j≥20。而i、j的上限的确定应根据我们研究范围酌情处理。我们暂主观约定 22≤i≤32，20≤j≤30。

我们对重庆市的初婚年龄人口随机抽出4000对进行观察，同时扣除部分法定年龄以外的对数和女性33岁以上的对数后，得到该市部分初婚年龄状况列联表抽样调查统计资料如表1。

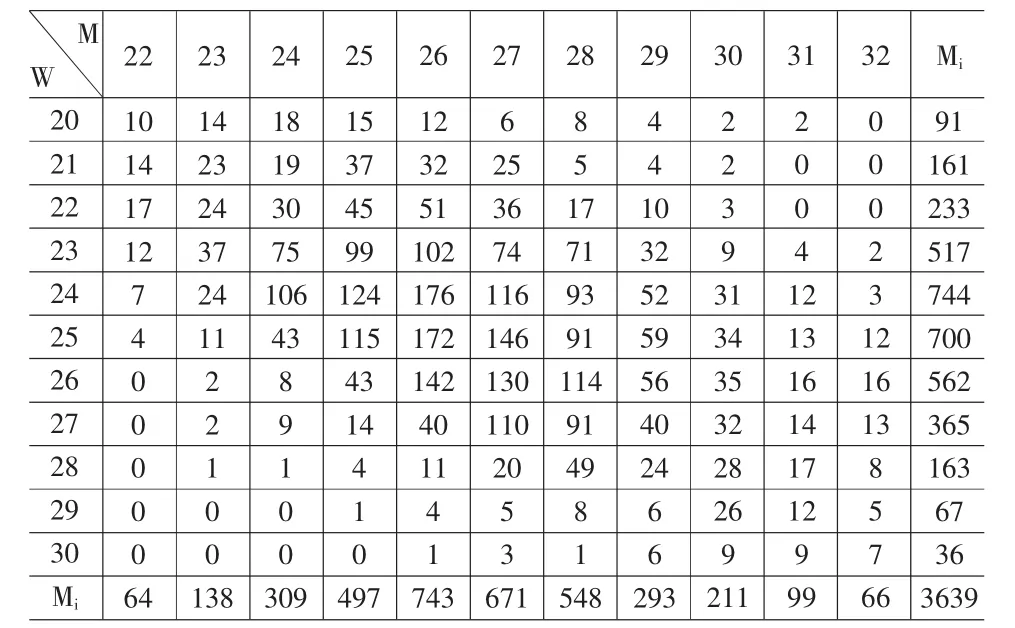
表1 初婚年龄配对调查资料

表1中第一行，第一列中的数据表示年龄，M表示男性，W表示女性。其他各行、各列分别表示各年龄组不同性别配对的对数。行为男性年龄组，列为女性年龄组，分别记为(i)，(j)。取出表1中的最后一列组成女性分布表，将表1中的资料简化成为两个表如表2、3。

表2 女性初婚年龄分布表

表3 男性初婚年龄分布表

由表1、表2、表3中的数据可知，初婚择偶意向分布规律与正态分布模型很相似（见图1，图2）。

根据上述资料结构和散点图的分析研究，可以比较清楚地看出初婚年龄择偶意向模型应当选择正态分布模型：

根据表2和表3中的数据，由期望、方差公式分别求得女性正态分布曲线参数μ1=24.63，δ12=4.05；男性正态分布曲线参数 μ2=26.71，μ22=4.36。

1.2 初婚意向模型偏度和峰度分析

为准确分析初婚意向模型的分布特征，我们对数据结构进行以正态分布为参照的偏度好峰度分析。

(1)模型偏度分析：偏度是描述某变量取值分布对称性的统计量，刻画了以平均值为中心的偏向情况。

(2)模型峰度分析：峰度是描述某变量所有取值分布形态陡缓程度的统计量，测度了数据在均值附近的集中程度，它是和正态分布相比较的。

计算得到各个参数如表4。

表4 初婚择偶意向偏度与峰度分析

从表4的数据分析可知，男性和女性的分布都接近于正态分布。女性婚配的概率分布为右偏，长尾拖在右边，男性婚配的概率分布也是如此，但男性的偏移程度更大；女性婚配峰度要比正态分布的高峰平缓，男性也是如此，但男性更加平缓，即其数据在均值附近的集中程度不如女性。因此，我们可以选择正态分布模型来进行近似拟合。

1.3 男性与女性初婚年龄分布模型

虽然男性和女性的分布情况与标准的正态分布模型有一定的差异，但是十分近似于正态分布模型。因此，可用正态分布模型进行拟合。男性和女性的分布模型如下：

（1）女性初婚择偶模型

由表2中的数据可得：

其中：pw(i，xj)表示女性在i年龄组上的分布函数，且有0≤pw(i，xj)≤1；xj为女性年龄变量，且 20≤xj≤30；i为第 i组男性，i=22，23，24，…，32。

又设：

由积分的几何含义可得Ww为分布曲线pw(i，xj)dxj在所考察区间内的总面积。

其中：i=22，23，24，…，32；j=20，21，22，…，30(i，j)表示为女性在i年龄组男性上的意向度,或称之为女性择偶系数。有：0≤(i，j)≤1 且：

其中：pm(j，xi)为男性在j年龄组上的分布曲线，且有0≤pm(j，xi)≤1；xi为男性年龄变量，且 22≤xi≤32；j为女性第 j年龄组，j=20，21，22，…，30。

又设：

这里的ywj是Wj的理论值。

（2）男性初婚择偶模型

由表3中的数可得：

由积分的几何含义可得：Wm为分布曲线pm(j，xi)在所考察的区间内的总面积。

其中：i=22，23，24，…，32；j=20，21，22，…，30。

pm(j，xi)表示为男性在j年龄组女性上的意向度，或称之为男性择偶系数。

显然有：

ymi为 mi的理论值。

1.4 初婚择偶模型解释及分析方法

1.4.1 模型的意义及初婚择偶意向度

曲线 pW(i，xj)和 pm(j，xi)分别说明了在 j，i的年龄区间内各性别的初婚择偶意向的分布情况。而是一个系数，用（即20岁到30岁的女性人数总和）后就可得到女性在这个年龄组上结婚的人数。同理，由乘以后就可得到男性在i年龄组上的人数。与此同时，具有十分重要的意义。它说明男女性别之间所存在的一种亲合程度或吸引程度的大小，即初婚年龄择偶意向度。显然，年龄择偶意向是一种倾向性，它表示的是人们的一种主观的心理倾向。从建立的正态模型可以看出这是与我国婚姻状况的实际情况相符合的。通过模型，我们将离散型的数据pm(j，xi)，pw(i，xj)转化成为连续型的数据。

1.4.2 初婚差位的定义及其分析

在 pw(i，xj)和 pw(j，xi)中的两个参数 μ1，μ2是人们比较关注的问题。它的社会意义是：μ1表示女性结婚的平均年龄，同时也表示女性结婚年龄的期望值。但由于正态分布的特殊性，它同时也表示女性在μ1时结婚的人数最多，即众数（即μ1为女性结婚对数的众数）。对于μ2来说具有同样的意义。不同时期，不同地区中μ1，μ2都不相同。在同一时期，同一地区μ1与μ2的差额，即μ1-μ2称为婚龄差位。

始龄差位是人们最感兴趣的问题，也是社会学家们在分析婚配情况时常用的方法和依据。绝大多数夫妇年龄之间都存在着一定的差异。在本案例中不存在此差异的仅占16%。一般来说，男性倾向于在比自己年轻的女性中寻找配偶，女性的情况则正好相反。从单个婚姻看，女性婚姻年龄大与男性婚姻年龄的情况并不鲜见，但从总体上看，世界各地区男性平均初婚年龄都大于女性平均初婚年龄（见表5）。

因而利用男女平均结婚年龄差计算得到的相对性别比更能反映各年龄组男女人口在婚姻市场上的情况。所以，在婚姻市场分析中常依据男女结婚年龄差来计算相对人口性别比，并以此来考察婚姻市场是否存在挤压问题。

通过计算性别比我们可以分析婚姻市场存在的问题是男性婚姻挤压，还是女性婚姻挤压。当婚姻市场男性供给大于需求，即出现男性过剩与女性短缺时，称之为男性婚姻挤压；反之，当婚姻市场中男性供给小于需求，即出现男性短缺与女性过剩是，称之为女性婚姻挤压。就目前中国整个婚姻市场来看，在中青年组人口中容易出现男性婚姻挤压现象，而中老年组人口中则易产生女性婚姻挤压问题。因此，在通常情况下，在一个人口中既存在部分年龄段的男性处于婚姻挤压中，同时也存在部分年龄段的女性处于婚姻挤压中。这种算法也有自己的缺点，它只是将已婚（有偶）人口加以计算来推测现在婚姻市场，可能会掩盖婚姻市场上的供需矛盾。因此，我们会在后面进行更深层次的分析，以弥补这一缺陷。

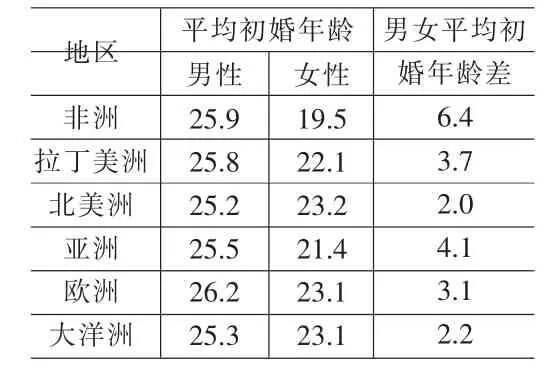
表5 世界各地区初婚婚龄差比较分析表

1.4.3 男性和女性最佳结婚年龄段分析

我们还可以从表（2）、表（3）中得出男性和女性的最佳结婚年龄段。我国平均结婚年龄1949年为18.57岁，1992年提高到22.50岁。目前，一些发达国家和发展中国家的发达地区，人们的实际平均结婚年龄，都普遍高于法定结婚年龄，并且日益推迟。对本次得到的调查数据进行初步的分析可以反映出：女性结婚年龄比例主要集中在23～26岁，其占了样本总量的69%，男性结婚年龄比例主要集中在25～28岁，其占了样本总量的68%；女性的最佳结婚年龄为24.6岁，男性的最佳结婚年龄为26.7岁。通过男女年龄比较可以看出，女性结婚年龄普遍比男性小。

1.4.4 交替分布法

2 初婚择偶意向分析方法应用

应用上述模型，我们可以对于初婚择偶意向进行多角度的分析。

2.1 模糊聚类分析

模糊聚类分析是一种建立分类的多元统计分析方法，它能将一批样本（或变量）数据根据其诸多特征，按照在性质上的亲疏程度在没有先验知识的情况下进行自动分类，产生多个分类结果。类内部的个体特征上具有相似性，不同类之间个体特征的差异较大。由pw，11或pm，11直接计算得到模糊相似关系矩阵或。以揭示在一定时期内多大年龄的女性或男性结婚率较高。

2.2 各年份结婚对数预测分析

用 pw，11，pm，11来对某地区的男女性适龄青年进行婚配分布来预测在各年份内当年的结婚对数，以解释大龄青年结婚难产生的原因和结婚夫妇对商品的各种需求量等，从而推动我们的计划生育工作和商品生产。同时，也有助于分析中国婚姻市场中的婚姻挤压问题和婚配年龄结构及其变动趋势。

2.3 女性与男性可缩程度评价分析

用pm，n，pw，n来对某地区的男女性进行配对分析，从而揭示某地区的性比例问题。其中：n为整个地区年龄的最大值。当然，n的大小也可以根据我们实际问题的需要而取定为一个适当的范围。

设：

其中：wi为第i年龄组的女性人数。

其中：mi为第i年龄组的男性人数。

当用 pw，n，pm，n作用于 Wn，Mn时可得到某一年龄组匹配的人数，也可说明在某地区，某时期各年龄组结婚人数的总和，以比较是否男女性比例失调等。通过下式来进行分析。

男性婚配对数分布矩阵Qm为：

女性婚配对数分布矩阵Qw为：

若我们定义：

则有：

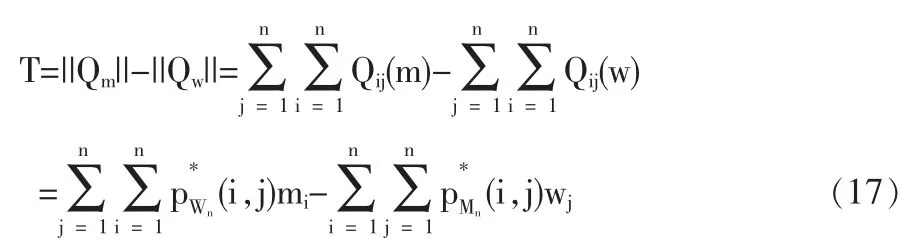
T为性别差,是用来比较男性多还是女性多的指标。还可以揭示出是什么年龄组的男性多还是女性多。对于多出来的值还要进行推移分析等。这种方法比起那种单纯地把某一年龄范围内的男性或女性加总起来进行比较其多少的方法来说更科学，更具有实际意义。

显然：T>0，男多于女；T＜0，女多于男。

对于长时期的分析还可以得到T值在什么区间内时为允许范围，视为正常；反之为不允许范围，即不正常，将会出现性比例失调等社会问题。特别是要通过分析研究找出全社会的性比例可缩程度值是十分重要的。

所谓性比例可缩程度，是指某地区，某时期内全社会性别差人数的绝对值占全社会范围内的人口总数的比重。即：

其中：｜T｜为性别差的绝对值，S为全社会人口总和。

可缩程度公式还有另外两种形式：

Gm为男性可缩程度，它表明性别差占男性全社会总数的比重。

GW为女性可缩程度。它表明性别差占女性全社会总数的比重。

对于G值的评价为：G值越大则说明性比例越不合理，可缩程度就越大；反之，则可缩程度小，性比例越趋于合理。

对于Gm来说，若Gm正值得越大则男性比例越大，因而男性的可缩程度就大，出现男性过盛；相反，则说明趋于合理。若Gm为负值，其绝对值越大则说明女性比例越大，因而女性的可缩程度就大，出现女性过盛；相反，则说明趋于合理。

对于GW来说，GW正值得越大，女性的比例越小，则男性过盛越严重，正值越少越合理；GW为负值，其绝对值越大则女性过盛越严重，绝对值越小而越趋于合理。

但是，上述两种可缩程度在什么值的情况下全社会的比例才合理，要由具体的时期、地区来确定，不能一概而论。

3 择偶意向影响下的性别比测算实证分析

3.1 分析思路

利用婚配对数矩阵进行婚配性别比的更深层次的分析，以此来分析中国婚姻市场。婚姻性别比是指婚姻市场中人们按照理想夫妇结婚年龄差模式（即传统的择偶年龄规范）择偶，可供选择的男性人口与可供选择的女性人口之比。而年龄别婚配性别比是指不同年龄的男性或女性可供选择的异性人口之比。

3.2 测算分析方法

在本案例中我们可以分析数据得到理想夫妇的年龄差见表6和图3。

表6 理想夫妇年龄差分布表

从图3中我们可以更直观地看到理想夫妇年龄差(M-W)为0～4岁的比例较大，由于大多数人在择偶时依旧守着“男高女低”的传统婚配标准。随着“老夫少妻”的现象越来越严重和“男大女小”的保守观念导致各个年龄段的男性共同去选择年轻的女性，这样就使得男性婚姻挤压的问题越来越严重，同时也导致在中老年的女性中的女性婚姻挤压现象越来越严重。

对i岁组男性而言，其婚配性别比为i岁男性选择的理想婚龄差的女性人口之比，即

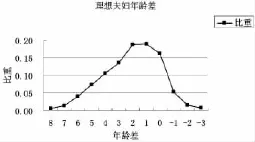
图3

其中：mi为第i年龄组男性人数；wj为第j年龄组女性人数；l为理想婚龄差；Ii-j为理想婚龄差的比例

同样，j岁女性婚配性别比为可供j岁女性选择的理想婚龄差的男性人口与女性人口之比，即

以上计算的是年龄别男、女婚配性别比，它反映的是不同年龄的男、女人口的婚姻挤压程度。然而，对整个婚姻市场来说，其婚配性别比为婚姻市场所有可供选择的男性与所有可供选择的女性之比，具体定义如下：

3.3 实证分析

下面我们以2005年全国1%人口抽样调查数据（见表7）为案例来对中国未来的婚姻市场进行分析。现将男女人口的结婚年龄分别限定在22～32岁与20～30岁范围内，我们把理想婚龄差的范围限定在-1到5岁内，理想婚龄差的夫妇比例以重庆市的比例来对全国的婚配情况进行理想化分析。

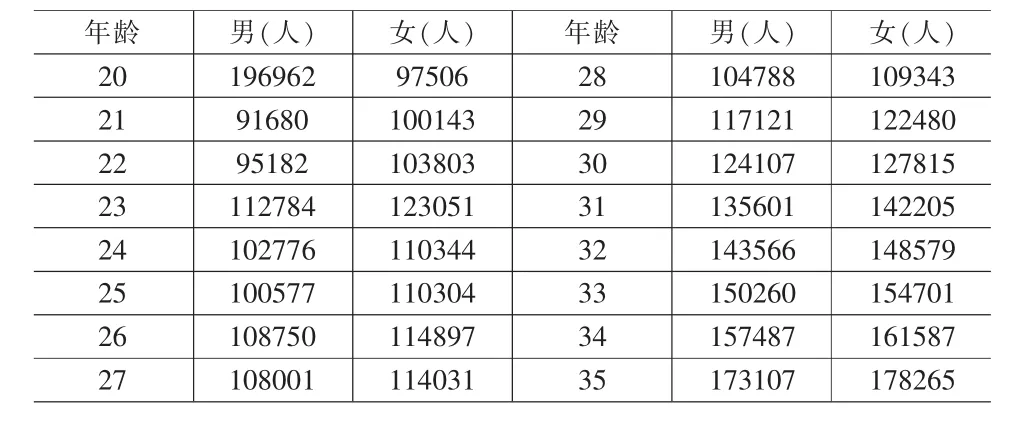
表7 2005年中国1%人口抽样调查资料

由前面的理论和公式可得，女性和男性的婚配性别比的情况见表8和表9。

从女性婚配性别比的角度，我们可以清楚地看到男性的婚姻挤压情况的严重性。我们以24岁组来进行分析，其女性婚配性别比为87.64，它表示在100名可供24岁女性选择的理想婚龄差的男性人口中只有88名女性能够与其匹配，另外12名男性则无理想婚龄差的女性与其匹配，存在男性婚姻挤压。从表8、表9还可以看出女性28和30岁时存在女性婚姻挤压，同时也说明了大龄女性中存在女性婚姻挤压的问题。