最小报价单位与市场有效性检验
2010-07-23郭喜才
郭喜才
(上海财经大学 金融学院,上海 200433)
0 引言
1 方差率检验统计量
市场有效性检验一直是金融学研究的热点问题。而在研究这一问题时,随机游走检验扮演着重要的角色。回报率随机游走模型是重要的理性预期模型并被频繁的用来检验市场有效性(或弱式有效性)。关于随机游走检验研究,已经发展了很多重要的理论,如French和Roll(1986)[1];Fama和French(1988)[2];Lo 和 MacKinlay(1988)[3];Poterba 和 Summers(1988)[4];Jegadeesh(1991)[5];Wright(2000)[6]等。这些检验理论的发展都是基于价格是连续状态的随机过程这一基本假设。而在各国资本市场上,都会有最小报价单位的限制,交易系统将会把交易价格自动处理成最小报价单位的倍数来处理。因此,连续状态的随机过程只是价格过程的一个近似处理。而在不同最小报价单位机制下,由连续状态下的渐进理论发展而来的检验统计量是否还能够继续被用来检验市场有效性,需要进一步的展开研究。本文将重点集中在应用最为广泛的Lo和MacKinlay(1988)的方差率检验统计量,利用蒙特卡洛方法,研究在不同回报率分布假设下,股价最小报价单位对方差率检验统计量的影响。
股价最小报价(Tick Size)单位是指证券交易时由系统设置的使价格不连续的最小变化单位。它规定了两个不同顺序报价的最小距离[7]。目前,各主要证券市场主要有两类最小报价单位的使用方式:一类是规定了统一最小报价单位,即证券不论价格大小,一律使用统一的最小报价单位,如美国纽约和纳斯达克证券交易所、加拿大证券交易所等;另一类是对不同价格水平的证券设置不同的最小报价单位,如伦敦证券交易所、东京证券交易所等。而且全球各大交易所的最小报价单位有所不同。纽约和纳斯达克实施长达几十年的0.125的最小报价,多伦多也曾实施过0.05的最小报价。我国股票市场股票最小报价单位统一为0.01元。
Lo和MacKinlay(1988)利用渐进理论发展了方差率检验统计量(Variance Ratio Statistics Test)来对随机游走进行检验。并利用其检验了美国1962年至1985年共包括1216个周收益率时间序列的随机游走。检验结果正如其发表在The Review of Financial Studies(1988)的论文题目一样——美国资本市场价格并不服从随机游走。
方差率检验在理论上比较直观。Lo和MacKinlay(1988)主要是检验股票的对数价格是否满足如下随机游走模型,如方程(1):

logpi表示第i时间的对数股价。这里μ是漂移项,εi是扰动项且满足均值为0的序列不相关性质,同时也允许存在异方差特性(heteroscedastic)。其主要思路是,如果对数股价满足随机游走,那么,由渐进理论,序列{logp2n-logp2n-2}的方差就应该是收益率序列{logpn-logpn-1}方差的2倍,股价的q阶差分序列{logpqn-logpqn-q}就应该是收益率序列{logpn-logpn-1}方差的q倍。也就是说,序列{logpn-logpn-1}的方差随着q的增加而线性增加。因此,假设现在共有nq+1个对数股价,表示为logpj,j=0,1,2,…,nq。定义q阶差分后的方差比为:

方程(2)里的各项分别为:


根据渐进理论,统计量Z服从标准正态分布。当把扰动项εi的限制放宽以后,如假设εi是独立随机过程,考虑异方差过程等,则如下的统计量Z*将渐进服从标准正态分布。

2 最小报价单位对方差率检验的影响
本文将重点研究不同最小报价单位对方差率统计量的影响,主要通过对比在不同最小报价单位的情形下,检验统计量和标准正态统计量的尾部特征,也就是比较统计量的拒绝率。例如,对于正态分布的统计量X,其分位数为1.96时对应的拒绝率为5%,也就是Prob{|X|>1.96}=0.05。我们分别报告检验统计量在不同名义拒绝率水平下(10%,5%,1%)各自的拒绝率数值,进而说明最小报价单位对方差率统计量的影响。
2.1 最小报价单位对实际价格的调整模型
设pj为实际理论价格为存在最小报价单位下的观测价格,它们的关系为:
2.2 最小报价单位方差率检验的影响
由于最小报价单位改变了资本价格,而渐进理论很难对存在复杂非线性的进行理论上的证明。因此,为了说明最小报价单位对方差率的影响,我们采用蒙特卡洛的模拟研究方法。由于方差率(Z或者Z*)是在大样本下才接近标准正态缝补,为此,本文将产生10,000个随机价格序列,每个随机序列的长度为1,000的理论价格。实际观测价格根据2.1中的调整模型,依不同报价单位进行处理。同时为了说明均值μ的取值是否影响,本文将分别取μ=0.0001和0.0005进行实验,结果表明μ的变化不会对方差率检验产生显著的影响。
下面将分别对上述四个空假设进行实验研究,即收益率分别服从正态分布、t分布以及存在异方差的情况等三种假设下。
2.2.1 同方差空假设
假设收益率分布分别满足正态分布假设以及T分布假设,即分布为同方差情况。表1和表2报告了收益率在正态分布假设下,统计量Z和Z*随不同最小报价单位变化情况。表1和表2的均值设为0.0001,标准差分别设为0.01和0.05。为了说明均值是否影响检验结果,表3报告了均值为0.0005情形下的模拟结果。
从表1可以看出,随着报价单位的增加,方差率统计量Z和Z*的名义拒绝率值不断的上升,意即和标准正态分布的名义拒绝率值相差越来越大。从表1中可以看出,当没有人为规定报价单位时,统计量Z和Z*的拒绝率和标准正态分布的拒绝率非常接近,这满足方差率渐进服从标准正态分布的理论。当最小报价单位为0.01时,似乎没有明显的区别,只是有少量的增加。当报价单位从0.125到1之间变化时,统计量Z和Z*的拒绝率明显呈增加的趋势,也就说明这种情形下,统计量Z和Z*根本就不满足渐进正态分布,而如果继续使用统计量Z和Z*来对市场有效性进行检验,结果就不准确了。T分布空假设下的结果同正态分布,这里不再报告。
为了更加直观的说明问题,图1~图4分别代表标准差=0.01,μ=0.0001情况下,q=4时的统计量Z*的分布直方图。图1和图2分别为没有最小报价单位和最小报价单位为0.01元时的统计量Z*的分布情形,和标准正态分布没有明显的区别。而图3和图4为最小报价单位分别为0.5和1元时的情况,显然,图3和图4非标准正态分布。
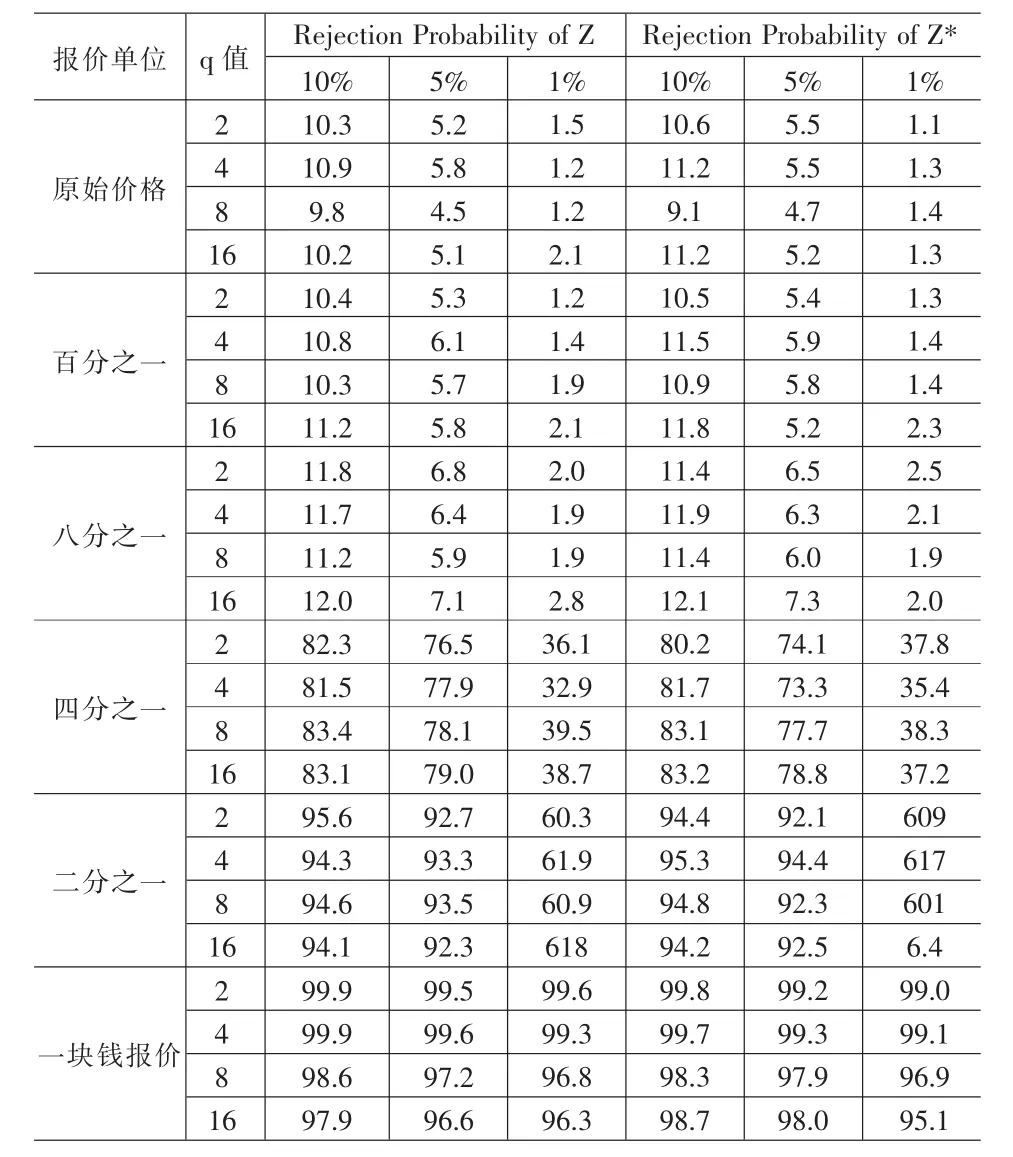
表1 标准差=0.01,μ=0.0001设定下的结果

表2 标准差=0.05,μ=0.0001设定下的结果
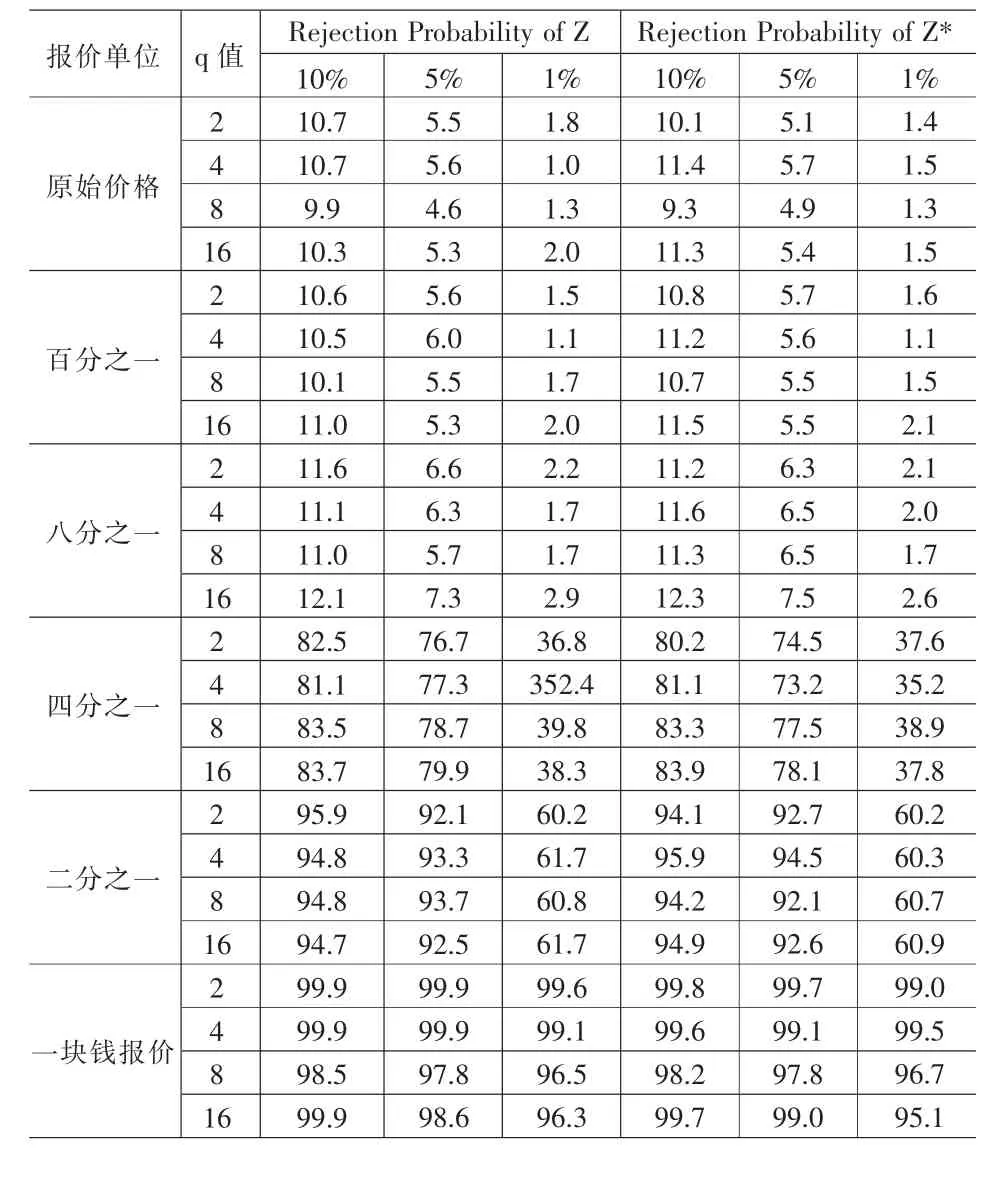
表3 标准差=0.01,μ=0.0005设定下的结果
2.2.2 异方差空假设
大量的实证表明,收益率的方差随时间变化而变化。最为著名的异方差波动模型为由Engle(1982)[8]发展而来的ARCH类模型。这个模型家族已经发展的十分庞大,为了说明问题,我们将采用在实证应用最为广泛的GARCH(1,1)(Bollerslev,1986)[9]和 EGARCH(1,1)(Nelson,1991)[10]模型。 即假设股价收益率是一个GARCH(1,1)或者 EGARCH(1,1)过程,最小报价单位对统计量Z和Z*产生怎样的影响。
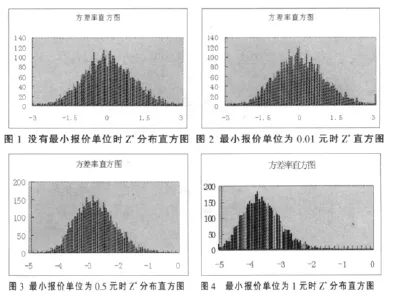
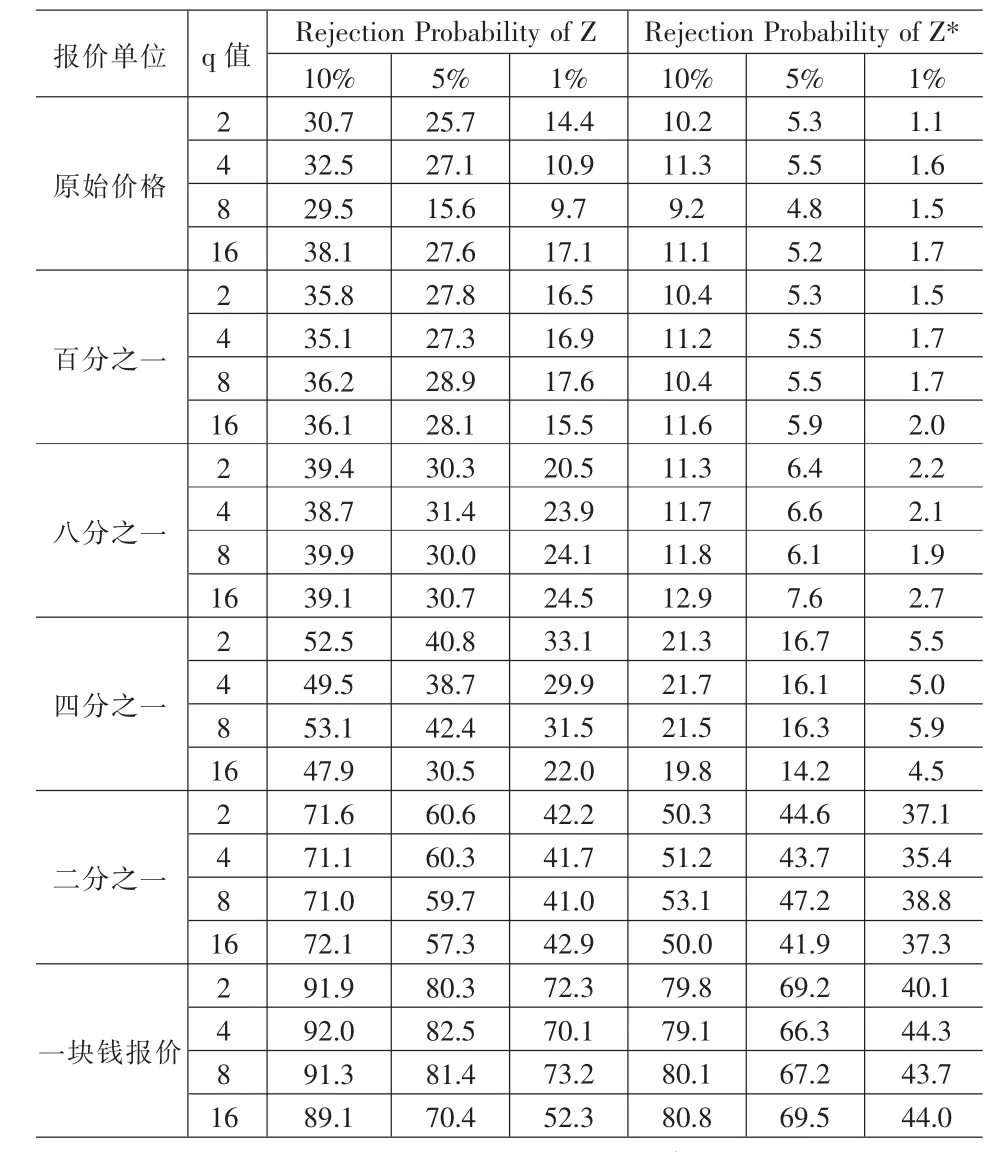
表4 标准差=0.01,μ=0.0005设定下的结果

zt是标准化以后的收益率,且满足标准正态分布,θ和γ为待估计参数,g(zt)是一个简单函数表达式。
表4为GARCH(1,1)情况下的模拟结果。根据表4,我们可以看到,随着报价单位的递增。统计量Z*的拒绝率逐渐上升,由于存在异方差情形下,只能用统计量Z*进行检验,因此,表4中的统计量Z没有任何意义。本文模拟结果表明,对于无条件波动率为0.05以及EGARCH等情形下,最小报价单位对统计量Z*拒绝率的影响大致相同,为了文章简洁,这里不予报告。
3 进一步讨论
对于方差率检验,需要进一步讨论。根据渐进理论,方差率VR(q)可以进一步表示为方程(5):


可以近似地写为:

显然,统计量~Z(q)和自相关系数有着非常紧密的联系。因此,本文的结论具有一定的普遍性。
总之,本文研究表明,最小报价单位对方差率(Lo和MacKinlay,1988)拒绝率将会产生影响。特别是当最小报价单位较大时,这一影响更加显著。因此,利用方差率来对市场有效性进行检验时,就需要考虑最小报价单位带来的影响。同时,也需要从理论上对检验市场有效性的理论进行进一步的研究,以便克服诸如最小报价单位等市场微观结构对检验统计量性质产生影响。
[1]French,K.,Roll,R.Stock Return Variances:the Arrival of Information and the Reaction of traders[J].Journal of Financial Economics,1986,(19).
[2]Fama,E.,French,K.Permanent and Temporary Components of Stock Prices[J].Journal of Political Economy,1988,(96).
[3]Lo,A.,MacKinlay,C.Stock Market Prices Do Not Follow Random Walks:Evidence from a Simple Specication Test[J].The Review of Financial Studies,1988,(1).
[4]Poterba,J.,Summers,L.Mean Reversion in Stock Prices:Evidence and Implications[J].Journal of Financial Economics,1988,(22).
[5]Jegadeesh,N.Seasonality in Stock Price Mean Reversion:Evidence from the U.S.and U.K[J].Journal of Finance,1991,(46).
[6]Wright.Alternative Variance Ratio Tests Using Ranks and Signs[J].Journal of Business&Economics Statistics,2000,(18).
[7]王春峰,卢涛,房振明.最小报价单位对我国股票市场流动性影响——基于高频数据的实证研究[J].系统工程,2005,(23).
[8]Engle,R.F.Autoregressive ConditionalHeteroskedasticity with Estimatesofthe Variance ofU.K.Inflation[J].Econometrica,1982,(50).
[9]Nelson,D.B.Conditional Heterosked Asticity in Asset Returns:A New Approach[J].Econometrica,1991,(59).
[10]Bollerslev, T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986,(31).
