基于巴克豪森效应的钢轨表面应力研究

王 平,杨雅荣,田贵云,2,姚恩涛,王海涛

(1.南京航空航天大学自动化学院,南京 210016;2.纽卡斯尔大学电子电力与计算机工程学院,NEI 7RU英国)

铁路客车行车密度、载重量和速度的不断提高,轨道故障也随之增多。钢轨受到车轮的挤压和温度影响,内部会产生局部的应力集中或松弛,从而导致钢轨局部或全部的塑性扭曲、变形,造成构件整体强度的降低,特别是构件疲劳强度的降低,从而造成事故隐患。因此,对钢轨各种缺陷,如应力、残余应力和疲劳寿命的检测有着十分重要的意义。目前,巴克豪森噪声(MBN)检测技术在无损检测领域得到了新的应用,可以对铁磁材料构件的应力、残余应力和微观结构进行检测,从而对铁磁性材料疲劳失效及寿命评估进行有效的诊断。在仪器制造方面,芬兰[1]的 Stresstech研制出了检测 MBN信号的μScan500C;德国弗劳恩霍夫无损检测研究所研制了微结构及应力分析仪(3MA-Ⅱ)等。笔者在此主要研究钢轨表面应力与不同特征值的对应关系,并分析温度因素对MBN信号的影响。

1 MBN原理和特征值

1.1 MBN检测原理

经多年研究[2]表明,对MBN信号直接产生影响的因素是材料的微观组织结构。决定和影响材料的微观组织结构的因素很多,比如材料的组成成分、受力、变形、热处理过程和环境温度等。这些因素都会直接或间接地决定或改变材料的微观组织结构,因此都会对巴克豪森信号产生影响。所以,可通过巴克豪森噪声方法检测材料的应力和微观组织结构。

20世纪30年代初,Bozorth和Dillinger等对巴克豪森信号进行了研究。测量了铁磁材料中巴克豪森跳跃脉冲信号的平均大小、数目和分布,并给出平均跳跃能量表达式为[3]：

式中L为接收线圈长度为跳跃产生的平均平方电流;Ur为可逆磁导率;A为线路常数;ρ为试样电阻率;BS=4πM,M为磁化强度为磁化密度变化率。MBN信号的大小除与接收线圈匝数L,磁化强度M有关外,还与跳跃产生的平均平方电流I2av有关,而的大小来自被测区域的内应力,热处理状态、晶格取向等因素与其有关。

1.2 特征值提取

巴克豪森应力检测中提取的特征值有五种,分别是均方根、平均值、振铃数、包络线和峰值时间。它们均能反映巴克豪森信号随应力和微观组织结构的变化关系。

1.2.1 均方根

噪声的强度通常采用均方根值来表示,即表征的是噪声的能量。均方根是研究噪声强度最普遍的一种方法。而MBN是高频噪声,所以笔者采用均方根来研究与压应力的对应关系。通过采样一定周期的信号后进行统计分析,计算信号的平方根均值,公式为：

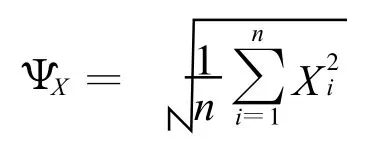
1.2.2 平均值

平均值是一个磁化周期中所有MBN信号被滤波后所形成包络线的幅值电压。由于MBN信号是随机信号,均应采用统计的方法,统计量越大其检测精度越高。采样一定周期的信号后进行统计分析,计算峰值电压的平均值,公式为：

1.2.3 振铃数

振铃数是在一个达到饱和磁化的周期中产生的幅值大于某一阈值的振铃个数,其值与阈值大小有关。即使是同一次检测,若阈值不同,其值的大小也不同。一般阈值应尽可能小,但应大于检测系统的噪声幅值或某些存在但幅值不大的干扰信号幅值。从微观理论上解释为MBN信号产生在激励信号上升和下降区。一个MBN信号是由无数多个180°磁畴壁翻转而成,它的外在表现形式是一次振铃(图1)[4],选择一个适当的阈值后,超过阈值的电压信号称为一次振铃,因此可以通过统计振铃数来评估与应力的对应关系。MBN振铃数与MBN信号溢出的强度密切相关,能够反映材料的应力和微观结构等信息。

图1 MBN振铃数示意图

1.2.4 包络线

包络线[5]是指激励信号上升周期或下降周期内一个MBN信号的轮廓。可以通过提取MBN信号包络线来评估材料的应力和微观结构等信息。MBN信号包络线包含峰值、峰值时间和半高全宽等信息,可更加准确可靠地评估出材料内部的微观结构,如材料内部的微小裂纹、腐蚀程度、应变和蠕变等信息都能通过包络线反映出来。

1.2.5 峰值时间

峰值时间是指MBN信号最大值的时间。在这里,横坐标为激励信号半个周期的时间域。如果激励信号频率为50 Hz,那么横坐标最大时间为10 ms,峰值时间即在10 ms内变化。在文献[1]中特征值峰值位置就是文中的峰值时间。

2 试验目的及方法

整个系统的硬件组成如图2,共分为五大部分：

(1)磁化器 函数发生器用于产生50 Hz、4 V的正弦波。LPA05B型功率放大器对正弦波信号进行功率放大。磁化器采用 U型磁芯,并采用直径0.25 mm的漆包线绕600匝。

(2)接收器 采用高频磁芯,0.13 mm漆包线绕5 000圈,并采用铜箔屏蔽。

图2 系统组成框图

(3)放大电路 由于MBN信号只有毫伏级,需对信号进行放大。

(4)数据采集和信号处理 采用DAQ-2010数据采集卡采集数据,在PC机的Matlab平台上进行处理,信号处理方法有带通滤波和小波去噪。

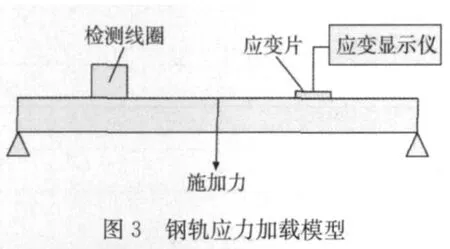
(5)应力加载设备 图3所示为钢轨应力加载模型,图4为钢轨应力检测图。

3 实际试验和结果分析

试验是在一段60 kg/m钢轨上手动加载压应力,在钢轨表面测量压应力与MBN信号对应关系,并提取MBN信号的不同特征值。在提取特征值前,笔者先对信号进行带通滤波,滤除低频和高频噪声,并对信号进行小波去噪。因为提取特征值采用的是统计方式,应尽量去除背景噪声和一切影响MBN信号幅值的噪声。

3.1 钢轨材料MBN信号的频带范围

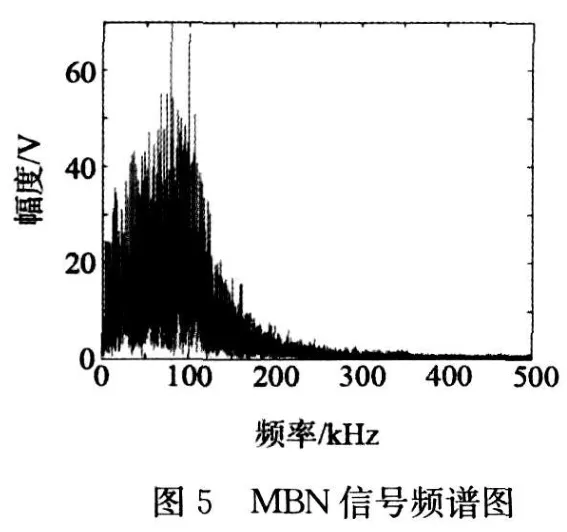
研究人员认为[6],MBN信号的频带为1 k Hz～2 MHz。通常一般材料在1～500 k Hz频段信号较丰富,且有明显依赖于显微组织、应力状态的变化的特征。图5是对信号FFT变换后的频谱图。从图5中可以看出,60 kg/m钢轨在100 k Hz时,MBN信号取得最大值。这与文献[7]研究结果相吻合。

3.2 不同特征值与压应力关系

3.2.1 均方根

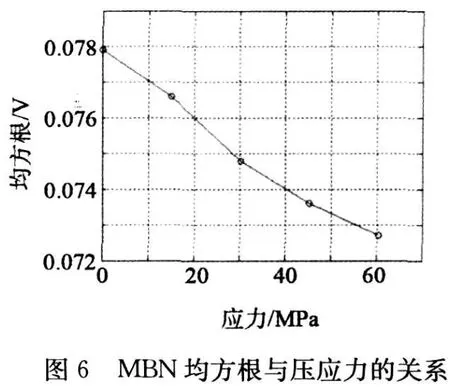
图6是MBN均方根与压应力的关系。均方根表征的是MBN强度,从图中可以看出,MBN均方根随着压应力的增大而减小,在60 MPa内具有比较好的线性关系。从磁畴理论解释为,当受压应力时,由于应力与磁畴的相互作用而产生附加磁弹性能,磁化方向趋向应力方向的畴缩小,磁化方向垂直应力方向的畴则扩大,当应力大到一定程度,则磁化方向垂直压应力的畴将会吞并其他方向的畴而成长至由90°畴壁分割的磁畴。而巴克豪森信号主要是由180°磁畴翻转而产生的,均方根主要与MBN幅值有关,180°磁畴随着压应力的增大而减少,故均方根也会随着压应力的增大而减小。

3.2.2 平均值

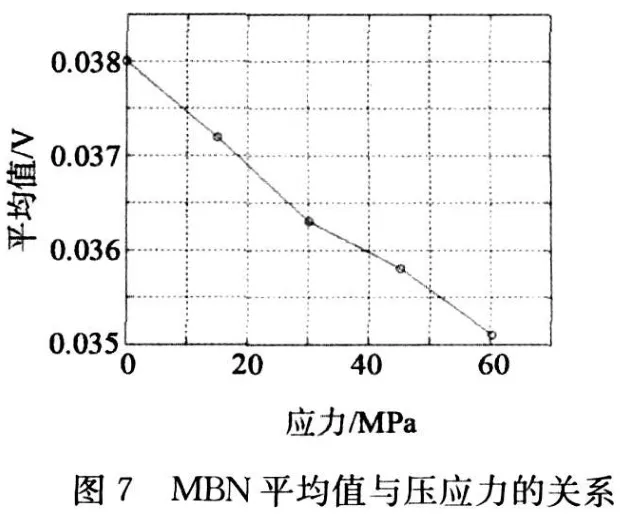
图7是MBN平均值与压应力的关系。从图中可以看出,MBN平均值随着压应力的增大而减小,在60 MPa内具有比较好的线性关系。磁畴理论解释原因如上节。MBN平均值实际上就是MBN峰值平均,所以平均值能更加直观地表示出了噪声的幅值大小。

3.2.3 振铃数

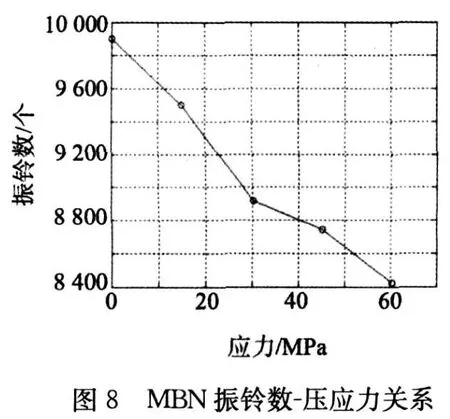
图8是MBN振铃数与压应力的关系。从图中可以看出,MBN振铃数随着压应力的增大而减小。MBN振铃数表征的是180°磁畴翻转的数量,磁畴翻转数量与材料内部的磁畴数量和材料的几何尺寸密切相关,但起最主要因素的是阈值大小。笔者选择的是电压0.3 V,当阈值选得太低或太高,振铃数与应力的相关性都很差。所以,提取特征值振铃数的关键是选择阈值。由笔者经验可以得出,阈值的选择不要超过MBN信号最大值的三分之一,这样得出的曲线具有比较好的相关性。

3.2.4 包络线

图9是MBN包络线与压应力对应关系。从图中可以看出,包络线的峰值随着压应力的增大而减小。峰值时间随着应力变化存在一定的偏移。但包络线不仅能反映峰值大小,还能反映形状的变化。因为试验采用的是同一钢轨,而且钢轨内部比较均匀。所以MBN包络线仅能反映出峰值变化和峰值时间的变化。MBN包络线适用于研究不同热处理,以及不同微观结构所导致包络线形状的变化。

3.2.5 峰值时间

图10为MBN峰值时间与压应力的关系。从图中可以看出,MBN峰值时间随着压应力的增大而增大,具有一定的单调趋势。

3.3 归一化

为了便于分析不同特征值之间的关系,对不同特征值的结果数据进行归一化处理。在此对均方根、平均值和振铃数进行归一化处理,因为三个特征值均随压应力的增大而减小,具有相同的变化趋势。图11是不同特征值的检测值与压应力的关系曲线。从图中可以看出,在弹性范围内,MBN均方根、平均值和振铃数均与压应力呈单调趋势,随着压应力增大而减小,但变化快慢不同。不同特征值随压应力增加而变化的快慢反映了传感器在检测中的响应大小。响应大则检测灵敏度高,否则反之。从检测灵敏度的高低评价检测效果,其MBN振铃数更为优越。在60 MPa以内,MBN均方根和平均值与应力具有比较好的线性关系,但均方根和平均值的绝对变化量和相对变化量都比振铃数的要小。

图11 归一化结果

3.4 温度对MBN影响结果试验

众所周知,钢轨长期暴露在炎热的夏天,轨温会随着气温的升高而升高,且轨温高于气温20℃[8],而标定应力与MBN信号曲线是在常温下进行的。如果要在炎热夏天检测应力值,钢轨轨温会对信号产生影响,导致检测应力值不准确。不同的钢轨材料,温度对MBN信号影响关系也不同[9]。为了排除温度本身对MBN信号影响,有必要研究温度与MBN信号的关系。

笔者用红外测温枪实时检测钢轨表面温度。图12是温度对MBN均方根的关系曲线。从图中可以看出,MBN均方根随着温度的增加而减小,且呈比较好的线性关系。这样就可以依据温度对MBN信号影响关系,在不同温度条件下准确地检测出钢轨应力值。

图12 温度与MBN均方根关系

4 结论和展望

研究分析了60 kg/m钢轨表面应力和不同特征值的对应关系,得出如下试验结果：

(1)MBN平均值、均方根和振铃数都随着压应力的增大而减小,它们的变化率依次递增。

(2)MBN包络线包含MBN峰值和峰值时间两部分信息,可用来提取两部分信息评估应力大小。

(3)MBN峰值时间与压应力具有一定的对应关系,随着压应力的增大而增大,具有一定的时间延迟。

(4)除温度因素外,在其他因素不变的条件下,环境温度变化范围内,MBN均方根值随温度近似呈线性关系。通过此线性关系,可以在不同温度条件下在线检测钢轨应力。

通过提取不同特征值与应力的对应关系,可以用标定MBN幅值和应力曲线的方法来检测钢轨表面应力,为后续检测钢轨表面应力提供有利条件。监测钢轨固定区内的MBN信号和温度值来精确检测钢轨表面应力,可作为评价其是否存在超标应力的一种方法。

[1]Ali Sophian,Gui Yun Tian,Sofiane Zairi.Pulsed magnetic flux leakage probe for crack detection and characterisation[J].Sensors and Actuators A：Physical,Available Online29,August 2005.

[2]John W Wilson,Gui Yun Tian,Vaidhianathasamy Moorthy,et al.Magneto-acoustic emission and magnetic Barkhausen emission for case depth measurement in En36 gear steel[J].IEEE Transactions on Magnetics,2009,45(1)：177-183.

[3]余玉武.对照Barkhausen效应研究硅钢磁声发射源机制[D].武汉：武汉大学,1990.

[4]John Wilson,Gui Yun Tian.Pulsed magneto-acoustic emission sensor array for stress measurement and material characterisation[C].School of Computing and Engineering Researchers'Conference,University of Huddersfield,2006.

[5]Stewart D M,Stevens K J,Kaiser A B.Magnetic Barkhausen noise analysis of stress in steel[J].Current Applied Physics,2004(4)：308-311.

[6]刘明珠,杨从晶,于助,等.巴克豪森噪声在应力及疲劳损伤检测上的应用[J].哈尔滨理工大学学报,2001,6(1)：73-76.

[7]Lo C C H,Jakubovics J P,Scruby C B.Monitoring the microstructure of pearlitic steels by magnetoacoustic emission[J].Journal of Applied Physics,1997,81(8)：4069-4071.

[8]于石生,田浩.基于巴克豪森效应的无缝钢轨纵向应力测试[J].无损检测,2002,24(3)：93-95.

[9]田浩,于石生,赵小莹.利用巴克豪森效应测定钢轨纵向应力[J].材料科学与工艺,2004,12(2)：196-198.