L值Q-下半连续函数的性质及应用

左彦平



值-下半连续函数的性质及应用

左彦平

（五邑大学 数理系，广东 江门 529020）

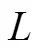
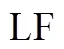
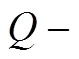
1 预备知识

证明 类似文献[4]中定理2.8的证明.

2 L值Q-下半连续函数

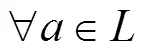
证明 必要性.显然成立.

证明 1）显然成立.

充分性.与定理3.4的充分性证明类似.

致谢 感谢导师白世忠教授的悉心指导.

[1] LOWEN R. Comparison of different compactness in fuzzy topological spaces[J]. J Math Anal Appl, 1978, 64: 446-454.

[2]杨忠强，杨乐成. 半同胚空间类[J]. 数学年刊，1988, 3: 324-329.

[3] BAI Shizhong. Fuzzy strongly semiopen sets and fuzzy strong semicontinuity[J]. Fuzzy Sets and Systems, 1992, 52: 345-351.

[4]白世忠. 拓扑分子格的弱分离公理[J]. 湘潭大学学报：自然科学版，1996, 18(3): 16-21.

[6]王银行，白世忠. 一些近似开集的等价性质[J]. 五邑大学学报：自然科学版，2008, 22(1): 5-9.

[7] BAI Shizhong. The SR-compactness in-fuzzy topological spaces[J]. Fuzzy Sets and Systems, 1997, 87: 219-225.

[8]王国俊.-Fuzzy拓扑空间论[M]. 西安：陕西师范大学出版社，1988.

[责任编辑：孙建平]

Properties and Applications of-valued-lower Semi-continuous Functions

ZUOYan-ping

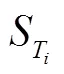
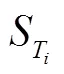
1006-7302（2010）01-0048-04

O189.1

A

2009-09-24

广东省自然科学基金资助项目（8152902001000004），江门市科技计划资助项目（江财工[2008]103）

左彦平（1974—），男，陕西宜川人，硕士研究生，研究方向：格上拓扑学，E-mail: zuoop@126.com.