混沌演化算法求解动态优化问题

王敏玲



混沌演化算法求解动态优化问题

王敏玲

（五邑大学 数理系，广东 江门 529020）

提出了一种结合混沌序列的演化算法——混沌演化算法，将其用于处理动态优化问题，并对动态多峰benchmark优化问题进行了数值实验，实验结果表明：混沌演化算法在处理动态优化问题时是有效的.

演化算法；混沌序列；动态优化

1 CEA算法

CEA的两个特点：

1）引入变异子群体. 群体划分为3部分，即记忆库+变异子群体+再初始化子群体，它们分别占群体规模的10%、5%和85%. 引入变异子群体的动机是：动态变化发生前，群体会收敛到目标函数的最优解或极值点附近；动态变化发生后，群体的个体显然不再是新情况下的最优解，但是将群体的部分个体保留并变异（这部分称为变异子群体），避免了历史基因信息的浪费，同时这部分基因信息有助于保持群体基因的多样性.

2）使用Logistic混沌序列. Logistic映射公式为：

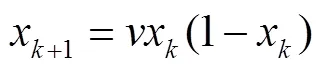
由该混沌映射系统产生的混沌随机数序列将替代系统伪随机数序列，满足算法中所有的随机数需求.

CEA算法步骤.

2）终止条件不满足时，反复进行如下操作：

b. 实行群体对变化的应激机制.

① 对再初始化子群体进行重新初始化；

② 对变异子群体进行变异；

③ 评估群体适应值.

② 更新记忆库.

2 数值实验

2.1 问题描述

表1 动态多峰benchmark问题5峰的初值

由此设置动态多峰benchmark问题模型的目标函数表达式为：

求解的目的是在可行域中寻找使目标函数取得最大值的最优解.

2.2 CEA参数设置及性能指标

为了验证算法的有效性，我们进行两个不同难度的实验.

A. 5峰的高保持初值为50，峰宽和坐标根据公式（2）动态改变；

B. 5峰的高、宽和坐标同时依据公式（2）动态改变.

2.3 实验结果及分析

实验A的5个峰高保持为50，所以目标函数的5个极值均为最大值；实验B（即动态多峰benchmark优化问题）的5峰动态改变，5个极值中有且仅有一个最大值. 所以实验A的难度较低，CEA搜索到最大值的可能性也较大.

上述两实验通过VC软件编程得出数值实验结果，并将数值实验结果在MATLAB6.5软件中绘制成曲线图.

图1 实验A的离线性能曲线图

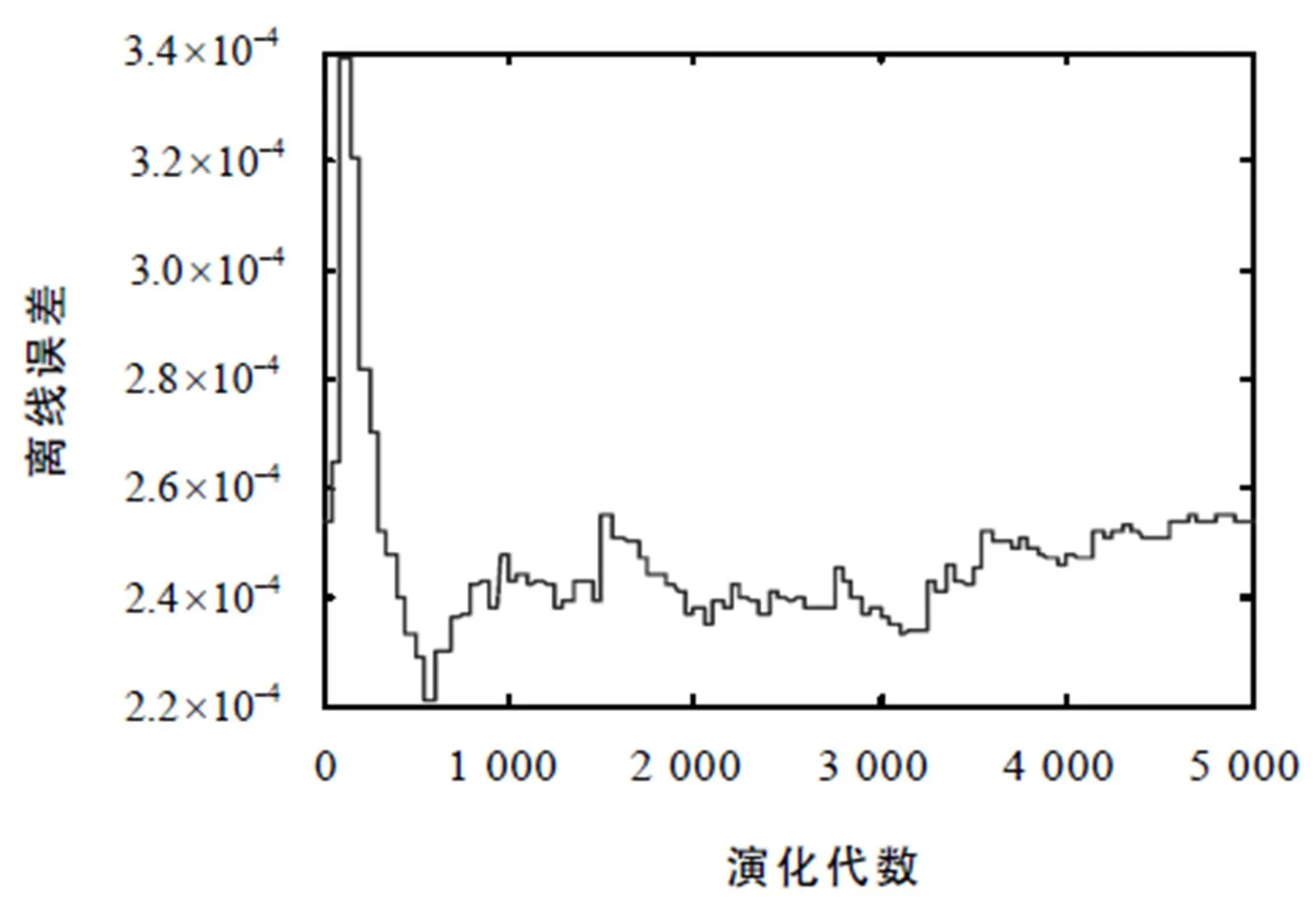
图2 实验A的离线误差曲线图

图3 实验B的离线性能曲线图

图4 实验B的离线误差曲线图

3 结语

本文结合混沌策略提出了混沌演化算法，并用新算法求解基于两个不同难度的动态多峰benchmark优化问题，得出了它们的离线性能和离线误差两个收敛性指标，实验结果表明：CEA具有良好的收敛性和稳定性，验证了CEA求解动态优化问题是有效的.

[2] CLAUS N B, THIEMO K. Dynamic memory model for non-stationary optimization[C]//Proceedings of the 2002

Congress on Evolutionary Computation. [S.l.]: IEEE, 2002: 145-150.

[3] RICCARDO C, LUIGI F, STEFANO F, et al. Chaotic Sequences to Improve the Performance of Evolutionary Algorithms[J]. IEEE Transactions on Evolutionary Computation, 2003,7(3): 289-304.

[4]DETERMAN J, FOSTER J A. Using chaos in genetic algorithms[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington: IEEE, 1999: 2 101-2 104.

[责任编辑：孙建平]

A Study of Dynamic Optimization Problems Based on Chaotic Evolutionary Algorithm

WANGMin-Ling

An algorithm combined with a chaotic sequence for dynamic optimization problems proposed: the chaotic evolutionary algorithm (CEA). Related numerical experiments on a moving peaks function benchmark problem are performed and the results demonstrate the effectiveness of CEA.

evolutionary algorithm; chaotic sequence; dynamic optimization

1006-7302（2010）01-0044-04

TP301

A

2009-09-25

五邑大学青年科研基金资助项目（A200709）

王敏玲（1981—），女，河南南阳人，助教，硕士，研究方向：智能计算，E-mail: ladywml@163.com.