ARIMA模型与Holt-Winters模型在铁路旅客周转量预测中的比较
2010-07-13万洁
万 洁
(济南铁路局 日照站,山东 日照 276826)
通过铁路旅客周转量预测客运量是铁路旅客运输组织工作的重要基础和主要依据之一。客运量短期预测主要是以一段时间内月度甚至日客运量的变化为出发点,研究短期内的客运量变化情况。短期客运量是一个存在季节和周期变化趋势、并存在一定增长 (或降低) 趋势的非平稳时间序列,为此分别运用ARIMA和Holt-Winters这两种典型时间序列预测模型,对我国2004—2008年铁路旅客周转量的月度数据进行拟合,在此基础上对2009年的月度数据进行预测,并与2009年各月份的旅客周转量实际值进行比较,分析两种模型预测的优劣。
1 ARIMA模型
ARIMA (Autoregressive Moving Average) 模型即自回归移动平均模型,适用于各种领域的时间序列分析,由博克斯—詹金斯 (Box-Jenkins) 于1976年提出,其建模思想是将预测对象随时间推移而形成的数据序列视为一个随机序列,构成该时序的单个序列虽然具有不确定性,但整个序列的变化却有一定的规律性。
ARIMA( p,q) 模型包含一个自回归模型和一个移动平均模型。如果该时间序列 ut只有通过d 阶差分后才能够达到平稳,则模型成为ARIMA ( p,d,q) 模型;若同时还具有周期性变化的特点,那么该时间序列就为带有季节性的自回归移动平均序列。
1.1 自回归模型AR(p)
p 阶自回归模型记作AR(p),满足下面的方程:

式中:ut为时间序列,t =1,2,…,T;参数c为常数;φ1,φ2,…,φp为自回归模型系数;p为自回归模型阶数;εt是均值为0,方差为σ2的白噪声序列。
1.2 移动平均模型MA(q)
q阶移动平均模型记作MA(q) ,满足下面的方程:

式中:ut为时间序列,t =1,2,…,T;参数 μ 为常数;θ1, θ2,…, θq为 q 阶移动平均模型的系数;εt是均值为0,方差为 σ2的白噪声序列。
1.3 ARIMA模型的建模步骤
ARIMA (p,q) 模型包括了一个自回归模型AR( p)和一个移动平均模型MA(q) ,方程为:

式中的参数同式⑴和式⑵。博克斯—詹金斯提出了具有广泛影响的建模思想,可分为4个步骤:平稳化处理;模型的识别;参数估计检验;预测应用。
下面利用ARIMA模型,对我国铁路2004—2008年月度旅客周转量数据进行建模、拟合,并对2009年的数据进行预测。
1.3.1 平稳化处理
应用ARIMA模型对时间序列建模进行预测,是建立在原始序列是平稳随机序列的基础上的。平稳时间序列的直观含义是序列不存在周期性和趋势性变动,而实际工作中的时间序列往往具有周期性和趋势性变动,需要将其转变为平稳时间序列,即序列平稳化处理。差分是序列平稳化最常用的方法,而检验序列平稳与否的最常用和有效的方法为ADF (Augmented Dickey-Fuller) 单位根检验。
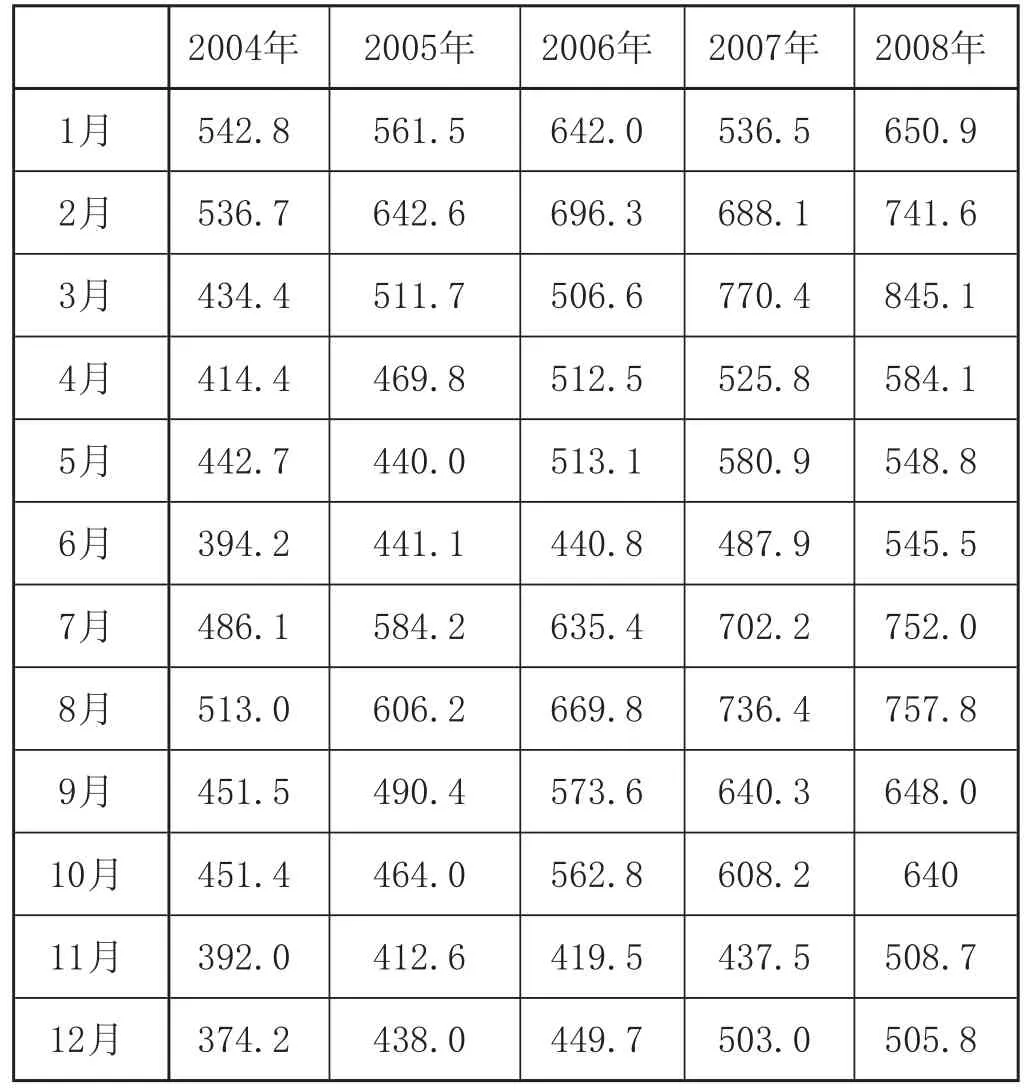
表1 2004—2008年我国铁路旅客周转量 亿人.km
从表1可以看出,随时间的变化,我国铁路旅客周转量的月度数据[1]序列 ( pt) 呈现缓慢上升趋势和季节周期波动 (周期为12个月,每年1—2月份和7—9月份旅客周转量达到高峰)。为了消除趋势同时减少序列的波动,首先对原始序列pt做一阶差分,生成序列dpt(其中:dpt=pt−pt−1)。
通过作dpt序列图可以看出,dpt序列的趋势基本消除,但季节性存在,因此对dpt序列再做一次周期间隔为12的季节差分,得到序列sdpt(其中:sdpt=dpt-dpt-12) 。sdpt的序列已经看不出季节性的痕迹。
对sdpt作ADF单位根检验,如表2所示。
检验结果说明,sdpt序列已经平稳,因而可以用于建模。

表2 对 sdpt 序列进行ADF单位根检验的结果
1.3.2 模型的识别
在建模时,需要利用自相关系数和偏自相关系数去识别ARIMA ( p,q) 模型。MA (q) 模型的自相关函数是 q 阶截尾的,而AR ( p) 模型的偏自相关系数是 p 阶截尾的。根据sdpt序列的相关图可以得出sdpt偏自相关系数2阶后截尾,因此取p =2,而自相关系数1阶后截尾,因此取q =1,由于进行了一次一阶差分,所以可以建立ARIMA (2,1,1) 模型,另外还要考虑季节差分的因素。
1.3.3 参数估计及检验
利用Eviews6.0软件对模型进行拟合,可以得到表3中各系数的估计值和整个模型的检验结果。从表3可以看出,模型各参数的估计值都通过了t 检验,而且整个模型调整的R2统计量为0.723,F统计量为37.554,D.W.值为2.33,也较为满意,模型残差的自相关图和偏自相关图也显示残差为平稳序列,说明模型很好地拟合了2004—2008年我国铁路旅客周转量的月度数据。
1.3.4 预测
经过模型识别、参数估计、模型检验以后,得到一个较好的模型,即可进行预测。在利用模型进行预测时,当然希望预测误差尽可能的小,最优的预测是具有最小均方预测误差的预测。利用ARIMA模型预测的2009年1—12月铁路旅客周转量的预测结果及误差见表4。

表3 ARIMA(2,1,1)模型的参数估计结果
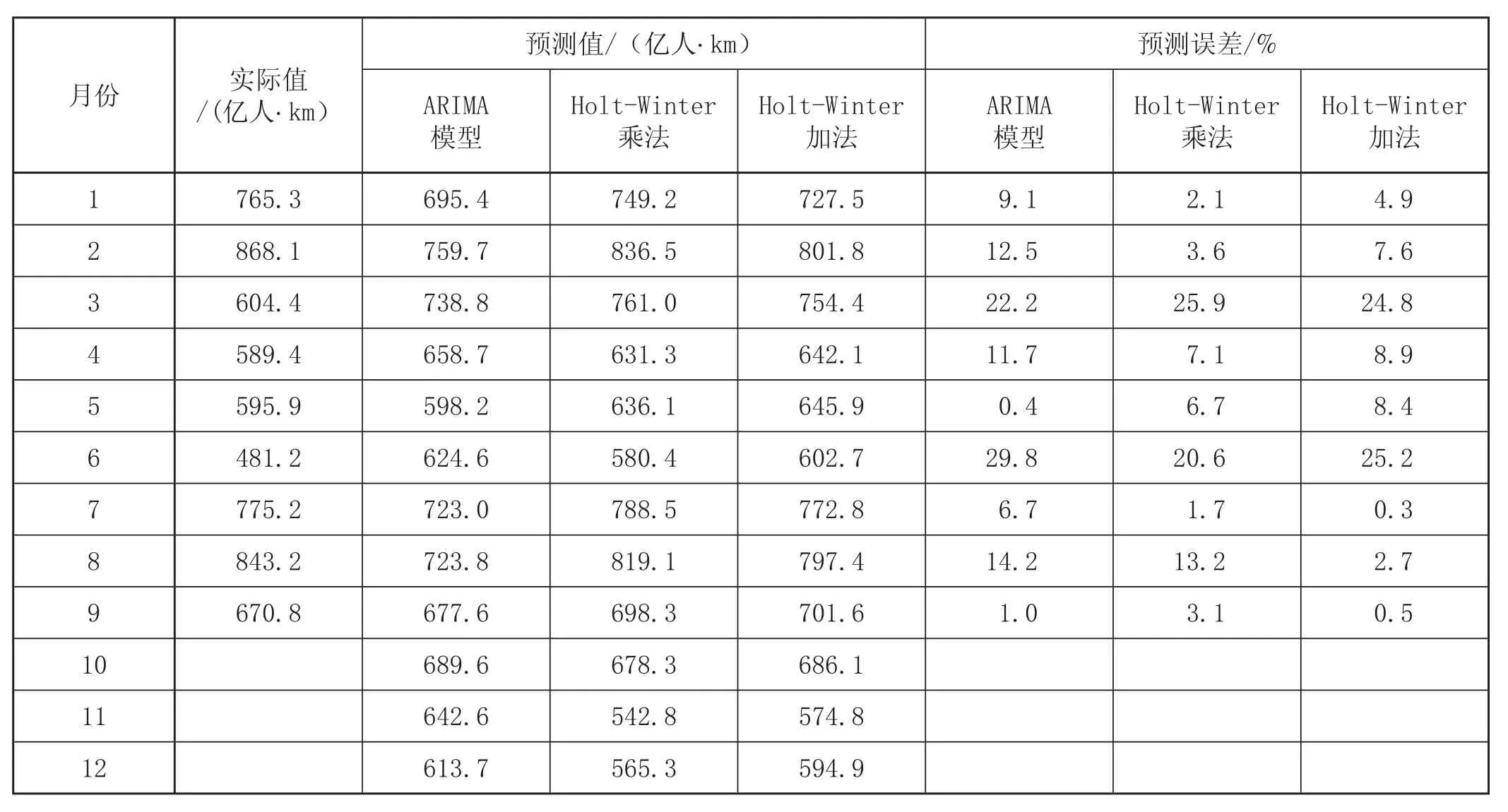
表4 我国2009年铁路旅客周转量预测值及误差
2 Holt-Winter模型
Holt-Winters模型[2]为指数平滑方法的一种,包括无季节模型和基于加法的季节模型,以及基于乘法的季节模型。由于铁路客运的月度数据均具有季节性,在此利用基于加法的季节模型和基于乘法的季节模型进行预测。
2.1 基于加法的Holt-Winters季节模型
基于加法的Holt-Winters季节模型适用于具有线性时间趋势和加法模型的序列。时间序列 yt平滑后的序列 y't由下式给出:

式中:a表示截距;b表示趋势;c为加法模型的季节因子;t = 1,2,…,T;k 为向后平滑期数,k > 0。
a,b,c的计算公式如下。
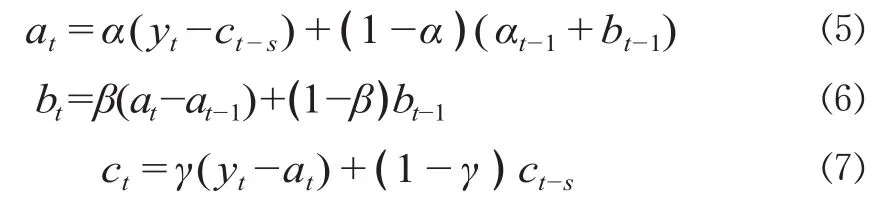
式中:α,β,γ为阻尼因子,在0~1之间;s 表示季节周期的长度,对于月度数据 s =12。
预测值由下式计算:

2.2 基于乘法的Holt-Winters季节模型
基于乘法的Holt-Winters季节模型适用于具有线性时间趋势及乘法模型的序列。时间序列 yt平滑后的序列 y't由下式给出:
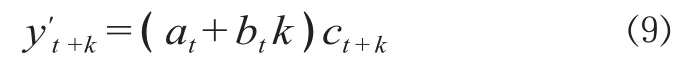
式中:a表示截距;b表示趋势;c为乘法模型的季节因子;t =1,2,…,T;k 为向后平滑期数,k >0。
a,b,c的计算公式如下。

式中:α,β,γ 为阻尼因子,在0~1之间;s 表示季节周期的长度,对于月度数据 s =12。
预测值由下式计算:
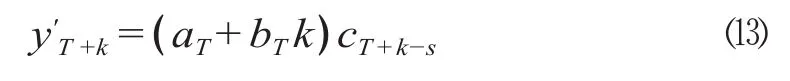
2.3 预测
利用Eviews6软件,分别选择基于乘法和加法的Holt-Winters季节模型,利用2004—2008年的铁路月度旅客周转量数据对2009年1—12月的数据进行预测。在预测时,Holt-Winters季节模型的 3 个平滑系数 a,β 和 γ 采用系统自定方式产生。利用基于加法和基于乘法的Holt-Winters季节模型预测的2009年1—12月铁路旅客周转量的预测结果及误差见表4,其中:预测误差=︱预测值-实际值︱/实际值×100%。
3 预测结果分析
ARIMA模型和Holt-Winters模型都属于短期预测模型,随着时间的推移,它们的预测效果也会逐渐变差。针对以上案例的铁路旅客周转量的短期预测,Holt-Winters 模型较ARIMA模型具有一定的优势,其原因可能在于Holt-Winters 模型所给出平滑参数可以采用系统自定的方法,系统通过多次比较给出的参数值往往是最优的。从实际操作过程发现,Holt-Winters 模型简便,而ARIMA模型的建模过程较为繁琐,而且在 p 和 q 的选择上存在着多种评判标准。
由于以上所采用的数据是全国范围的旅客周转量数据,而且受经济危机的影响,近期旅客运输量出现了较大的波动,而这两种预测方法都只是从序列本身出发,不考虑其他经济社会因素的影响,因此预测的误差较大。所以,各级旅客运输组织在对客运量做短期预测时,应适当地考虑影响客运量波动的因素,以提高预测的准确性。
[1] 铁道部统计中心. 全国铁路主要指标完成情况[EB/OL].[2009-11-02]http://www.china-mor.gov.cn/zwgk/zwgk_tjxx.html.
[2] 高铁梅. 计量经济分析方法与建模[M]. 北京:清华大学出版社,2006.
