如何用SAS软件正确分析生物医学科研资料VIII. 用SAS 软件实现拉丁方设计定量资料的统计分析

陶丽新，胡良平，郭晋



如何用SAS软件正确分析生物医学科研资料VIII. 用SAS 软件实现拉丁方设计定量资料的统计分析

陶丽新，胡良平，郭晋

100850 北京，军事医学科学院生物医学统计学咨询中心

编者按

生物统计学是生物学领域科学研究和实际工作中必不可少的工具，在分子生物学迅速发展的今天，生物统计学更显示出了它的重要性。实验设计与数据统计分析是现代生物学的基石，是生物学研究者检验假说、寻找模式、建立生物学理论的有利工具，也是生物学研究者探索微观和宏观生物世界的必备基础知识。对于每天甚至是每时每刻涌现的大量的、以天文数字计量的分子遗传数据，必须借助统计学知识加以分析处理，才能从中获得有意义的信息。“生物多样性数据分析”是开展生物多样性研究的一个重要方面，数据分析能力的高低极大地影响着我们对各种生态学现象认识的深度和广度。现在，电子计算机的普及使得生物统计分析过程大大简化，生物统计分析软件包的普及将生物统计学从统计学家的书本里解放了出来，简化了生物统计分析过程，使之成为生物学研究者的常用工具。本刊特邀军事医学科学院生物医学统计学咨询中心主任胡良平教授，以“如何用 SAS 软件正确分析生物医学科研资料”为题，撰写系列统计学讲座，希望该系列讲座能对生物医学科研工作者有所帮助。

1 拉丁方设计的概念及应用场合

拉丁方设计是当实验中只考察 1 个水平的实验因素，但同时又涉及 2 个都具有水平的区组因素（即重要的非实验因素），且它们之间的交互作用无统计学意义时所采用的实验设计类型。

正交拉丁方设计是在当实验中只考察 1 个水平的实验因素，但同时又涉及3 个都具有水平的区组因素，且它们之间的交互作用无统计学意义时所采用的实验设计类型，又叫作希腊拉丁方设计。

很显然，拉丁方设计和希腊拉丁方设计是根据实验所涉及到的区组因素的个数来区分的，有时候也将这 2 种实验设计类型分别称为三因素拉丁方设计和四因素拉丁方设计。

拉丁方设计适用于下列场合：若每个区组中的个数据取自条件相同或相近的个受试对象，那么实验因素对观测指标不会产生“携带效应”的影响，往往是以“较大的样本含量为代价的”。但是如果每个区组中的个数据重复测自相同的受试对象，虽然可以达到减少受试对象个数的目的，但是由于存在“携带效应”（前一种处理对观测指标造成的影响在受试对象接受下一个处理时仍然存在），使其一般不适用于干预性实验研究，除非能够保证实验因素各水平对观测指标的影响是短暂可逆的，即在设定的时间间隔内，前一种处理对观测指标的影响会消除，观测指标的取值会恢复到最原始的水平的观察性研究中应用拉丁方设计效果较好；拉丁方设计和正交拉丁方设计都要求实验所涉及的3 个或 4 个实验因素之间不存在交互作用或者交互作用可以忽略不计且各因素的水平数相同（以实验因素的水平数为基准）[1-2]。这2 类拉丁方设计的构造方法和列表格式参见下面的实例。

2 拉丁方设计一元定量资料方差分析的 SAS 实现

例 1 受试对象为 7 名志愿受试的健康女大学生，年龄在 19 ~ 21 岁，均有多次晕车史。正式试验前进行的运动病敏感试验证明她们确实为运动病敏感者，运动病耐力得分为（14 ± 7.4）分。药物及分组：安慰剂为淀粉片（100 mg/片·人）（A）；晕海宁（50 mg/片·人）（B）；山莨菪碱（10 mg/片·人）（C）；脑益嗪组（25 mg/片·人）（D）；晕可平（30 ml/人）（E），主要成分为黛赭石、车前子等；生姜合剂（30 ml/人）（F），主要成分为生姜、明天麻等；复方中西药制剂（G），每人使用上述生姜合剂 15 ml 加山莨菪碱 2.5 mg、脑益嗪 6.25 mg。药物均口服。

实验方法：①运动病诱发试验：被试者坐在电动转椅上，头部固定，然后按 A 程式、B 程式顺序进行反复急停刺激（采用“Modified Graybiel Method”[3]）。A 程式：被试者闭眼，作顺时针旋转，以 10º·s-2加速到 100º·s-2（10 s 内），恒速旋转 20 s，然后在 0.5 s 内急停，休息30 s，再重复进行，共 20 次；B 程式：被试者开眼，作逆时针旋转，参数同上，亦在 0.5 s 内急停，休息 30 s 后再重复进行，共20 次。以被试者感到恶心为终止点。耐受上述刺激 A 程式每次计 1 分，B 程式每次计 2 分。②被试者于饭后 1 h 进入实验室，按顺序给药。服药 1 h 后进行运动病诱发试验，计算被试者每次的运动病耐力得分。试验于每周六或周日进行，连续 7 周完成。设 7 种药物编号为A、B、C、D、E、F、G。7 名志愿者编号分别为1、2、3、4、5、6、7，如表 1 所示。

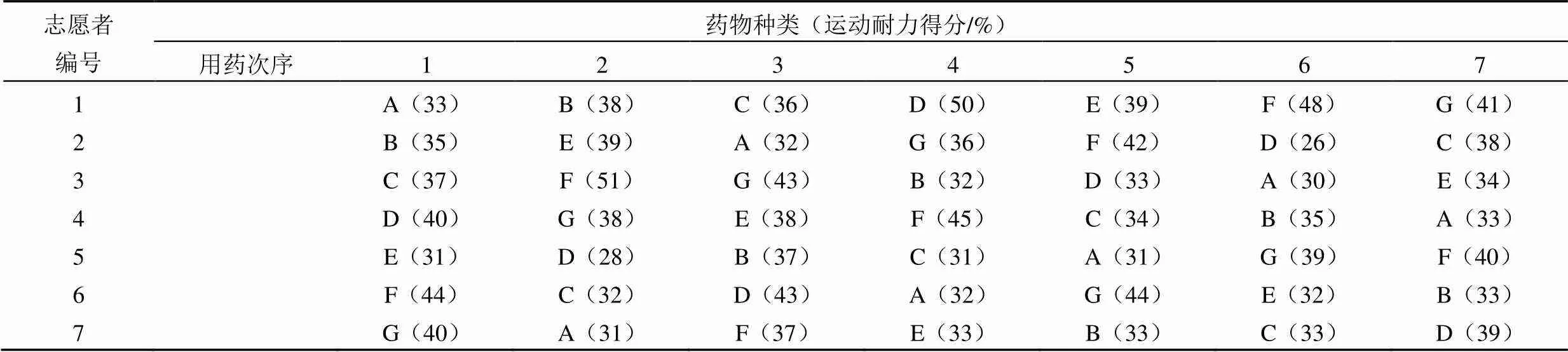
表1 不同药物、不同志愿者、不同用药顺序对运动耐力得分的影响

分析与 SAS 实现：该研究资料中，样本含量为 7，试验因素为“药物种类”，它有 7个水平；同时还涉及 2 个区组因素分别为“受试者的个体差异”和“用药次序”，分别有 7 个水平，并且因素之间的交互作用可以忽略不计，定量的观测指标为“运动耐力得分”，因此该资料应该为 7 × 7 拉丁方设计一元定量资料。

对于该类资料进行统计分析，首先检查资料是否满足方差分析的前提条件，若满足则采用 7 × 7 拉丁方设计一元定量资料的方差分析；若不满足，则可以采用适当的变量变换方法使变换后的资料满足方差分析的前提条件，然后再对变换后的资料采用 7 × 7 拉丁方设计一元定量资料的方差分析。需要注意的是，要处理好“携带效应”的问题，因为试验因素是药物种类，因此应该确保前一次用药对后一次用药的影响是微弱的，最好是在间隔一段时间后，定量指标的取值能基本恢复到原先的水平，原文试验每次用药间隔 1 周时间。

具体的 SAS 程序（注：检查资料是否具备参数检验前提条件的程序从略，下同）：

data a; do sub=1 to 7; do ord=1 to 7; input med $ value@@; output; end; end;cards;A 33 B 38 C 36 D 50 E 39 F 48 G 41B 35 E 39 A 32 G 36 F 42 D 26 C 38C 37 F 51 G 43 B 32 D 33 A 30 E 34D 40 G 38 E 38 F 45 C 34 B 35 A 33E 31 D 28 B 37 C 31 A 31 G 39 F 40F 44 C 32 D 43 A 32 G 44 E 32 B 33G 40 A 31 F 37 E 33 B 33 C 33 D 39;run;ods html;proc anova data=a; class sub ord med; model value=sub ord med; means med/snk;run;quit;ods html close;

程序说明：数据步建立数据集 a，输入变量名和变量值，“sub”、“ord”、“med”和“value”分别代表志愿者编号、用药顺序、药物种类和运动耐力得分。过程步调用适于分析均衡数据的方差分析过程，其过程名为 anova；class 语句指出在 anova 过程中要使用的分类变量；model 语句用来规定因变量和自变量效应；means 语句用来计算药物种类所对应的运动耐力得分的均值，snk 选项表示对 7 种药物使用后的运动耐力得分的平均值进行两两比较，quit 语句用来结束 anova 过程，因为 anova 过程为交互式的，run 语句不能结束该过程，它只是告诉 anova 去执行 run 语句之前的语句。

SAS 输出结果与结果解释：

SourceDFAnova SSMean squareF valuePr > F sub6205.7142857 34.28571431.980.1002 ord6 41.7142857 6.95238100.400.8722 med6696.8571429116.14285716.700.0001

从以上输出结果中可以看出，不同的受试者和不同的用药顺序分别对运动耐力得分均值影响之间的差异均无统计学意义，而不同的药物种类对运动耐力得分均值影响之间的差异则有统计学意义（= 6.70，= 0.0001 < 0.05）。

此处药物因素全部水平下均值之间的两两比较结果从略，依下面简化后模型输出的结果为准。

从第一部分输出结果中可以看出，不同受试对象和不同的用药顺序对运动耐力得分均值的影响之间的差异无统计学意义，可以在 SAS 程序的 class 和 model 语句中将 sub 和 ord 删除，这样可以增大误差项的自由度，使结果更加稳定可靠。重新运行程序，得到检验结果如下：

SourceDFAnova SSMean squareF valuePr > F med6696.8571429116.14285716.36< 0.0001

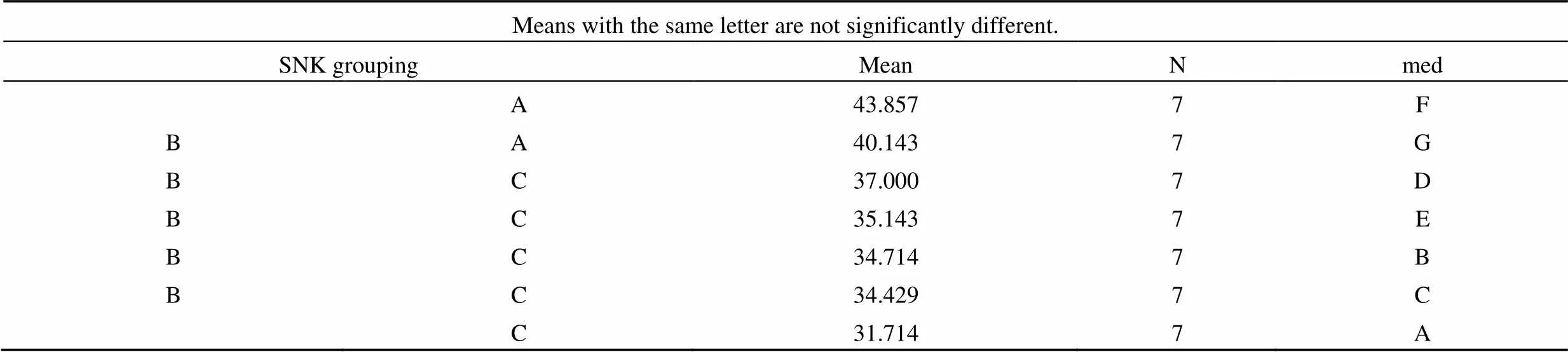
Means with the same letter are not significantly different. SNK groupingMeanNmed A43.8577F BA40.1437G BC37.0007D BC35.1437E BC34.7147B BC34.4297C C31.7147A

从以上结果中可以看出，生姜合剂组与安慰剂组、晕海宁组、山莨菪碱组、脑益嗪组、晕可平组以及安慰剂组与复方中西药制剂组的运动耐力得分均值之间的差异具有统计学意义，其他两两组之间的运动耐力得分均值之间的差异没有统计学意义。生姜合剂组的运动耐力得分均值明显大于安慰剂组、晕海宁组、山莨菪碱组、脑益嗪组、晕可平组的运动耐力得分均值；复方中西药制剂组的运动耐力得分均值明显大于安慰剂组的运动耐力得分均值。

例 2 在某项研究中，将4 种不同剂量的某药液分别注射于 4 个受试对象，每个受试对象先后接受此药物的不同的剂量各 1 次（即每个受试对象接受药物 4 次），资料如表 2 所示。

表 2 不同的给药次序、不同的受试对象、不同的药物剂量对血糖升高值的影响

分析与 SAS 实现：该资料中样本量为 4，试验中涉及 1 个试验因素，即“药物剂量”，它有 4 个水平；同时还涉及 2 个区组因素：“给药次序”和“受试者编号”，均有 4 个水平，且交互作用可以忽略不计，定量观测指标为“血糖的升高值（mg/dl）”，因此该资料为 4 × 4 拉丁方设计一元定量资料。

先检查资料是否满足参数检验的前提条件，若满足，则采用 4 × 4 拉丁方设计一元定量资料的方差分析；若不满足，则采用适当的变量变换方法使变换后的资料满足方差分析的前提条件，然后再对变换后的资料采用 4 × 4 拉丁方设计一元定量资料的方差分析。

具体的 SAS 程序：

data b;do ord=1 to 4; do sub=1 to 4; input med $ value@@;output; end; end;cards;C 42 B 96 A 53 D 110B 50 A 31 D 78 C 55A 50 D 64 C 55 B 70D 98 C 41 B 79 A 49;ods html;proc glm;class ord sub med;model value=ord sub med;means med/snk;run;quit;ods html close;

程序说明：该例资料的 SAS 程序与例 1 的程序唯一不同之处是：过程步调用了 glm过程，glm 过程主要用于对非均衡数据进行方差分析，均衡数据也可以使用该过程，此时，可比 anova 过程消耗更多的计算机资源。对该资料而言，2 个过程的 SAS 输出结果是基本相同的。

SAS 输出结果与结果解释：

SourceDFType III SSMean squareF valuePr > F ord31049.187500 349.7291671.530.2996 sub3 423.687500 141.2291670.620.6277 med34913.1875001637.7291677.180.0207

从上面结果可以看出，给药次序和受试者的个体差异对血糖升高值的影响之间的差别没有统计学意义，药物剂量对血糖升高值的影响之间的差异具有统计学意义（= 7.18，= 0.0207 < 0.05）。

此处药物剂量全部水平下均值之间的两两比较结果从略，依下面简化后模型输出的结果为准。

由于给药次序和受试者编号对血糖升高值之间的差别没有统计学意义，可以将 SAS 程序 class 和 model 语句中的 ord 和 sub 删除，这样可以使误差项的自由度增大，使结论更加可靠。重新编写程序并发送给系统执行，得到下面的检验结果：

SourceDFType III SSMean squareF valuePr > F med34913.1875001637.7291676.920.0059

Means with the same letter are not significantly different. SNK groupingMeanNmed A87.504D BA73.754B B48.254C B45.754A

从上面的结果中可以看出，该药物 D 剂量与 C 剂量对血糖升高值的影响之间的差别具有统计学意义，D 剂量组的血糖升高值明显高于 C 剂量组的血糖升高值；该药物 D 剂量与 A 剂量对血糖升高值的影响之间的差别具有统计学意义，D 剂量组的血糖升高值明显高于 A 剂量组的血糖升高值；其他任何 2 种剂量对血糖升高值的影响之间的差别没有统计学意义。

3 正交拉丁方设计一元定量资料方差分析的 SAS 实现

例 3 在应用重组人肿瘤坏死因子（rh-TNF）促进伤口愈合的实验研究中，欲比较其 5 种不同剂量的效应，同时要观察动物个体间、不同用药部位间、给药顺序间的差别。在该研究中，每隔 1 日更换内层敷料，滴药 1 次，记录伤口愈合时间：

表3中，在行间随机分配 5 只不同家兔，列间每只家兔背部切除位置不同的全层皮肤的 5 块 2 cm × 2 cm 创面，希腊字母为每次用药的 5 种先后顺序，拉丁字母代表 5 种不同用药滴数，即：A（0）、B（1）、C（2）、D（3）、E（4）。

分析与 SAS 实现：在该研究资料中，样本量为 5，试验因素为“重组人肿瘤坏死因子的剂量”，有 5 个水平；同时涉及到 3 个区组因素，分别为“家兔的个体差异”、“用药顺序”和“用药部位”，分别有5 个水平，并且因素之间的交互作用可以忽略不计，定量的观测指标为“家兔创面的愈合时间（d）”，因此该资料为 5 × 5 的正交拉丁方设计一元定量资料。

当资料满足方差分析的前提条件时，使用 5 × 5 正交拉丁方设计一元定量资料的方差分析；若不满足，则采用适当的变量变换方法使变换后的资料满足方差分析的前提条件，然后再对变换后的资料采用 5 × 5 正交拉丁方设计一元定量资料的方差分析。

表 3 家兔创面不同用药量的愈合时间（d）

具体的 SAS 程序：

data c; do sub=1 to 5; do buwei=1 to 5; input jiliang $ ord $ time@@;output; end; end;cards;A α 26 B β 21 C γ 20 D δ 17 E ε 18B δ 20 C ε 19 D α 18 E β 17 A γ 25C β 19 D γ 20 E δ 18 A ε 24 B α 20D ε 18 E α 18 A β 24 B γ 21 C δ 19E γ 17 A δ 24 B ε 21 C α 18 D β 17;run;ods html;proc anova; class sub buwei ord jiliang; model time=sub buwei ord jiliang; means jiliang/snk;run;quit;ods html close;

SAS 输出结果与结果解释：

SourceDFAnova SSMean squareF valuePr > F sub4 2.9600000 0.74000001.370.3257 buwei4 2.9600000 0.74000001.370.3257 ord4 3.3600000 0.84000001.560.2753 jiliang4161.360000040.340000074.70< 0.0001

从以上结果可以看出，家兔的个体差异、不同的用药部位、给药顺序对伤口愈合时间造成的影响之间的差异没有统计学意义，而药物的不同剂量对伤口愈合时间造成的影响之间的差异具有统计学意义（= 74.70，< 0.0001）。

此处用药滴数全部水平下均值之间的两两比较结果从略，依下面简化后模型输出的结果为准。

由于家兔的个体差异、不同的用药部位、给药顺序对家兔创面伤口愈合时间造成的影响之间的差异没有统计学意义，可以将 SAS 程序 class 和 model 语句中的 sub、buwei、order删除，重新运行程序，得到检验结果如下：

SourceDFAnova SSMean squareF valuePr > F jiliang4161.360000040.340000059.32< 0.0001

Means with the same letter are not significantly different. SNK groupingMeanNjiliang A24.60005A B20.60005B C19.00005C DC18.00005D D17.60005E

从上述结果中可以看出，用药滴数为“2（C）”与“3（D）”之间、“3（D）”与“4（E）”之间在家兔创面愈合时间上的差异没有统计学意义，其他两两之间比较的差异都具有统计学意义。用药滴数为“0（A）”组的创面愈合天数明显长于其他各组；用药滴数为“1（B）”组也明显长于“2（C）”以上各组；用药滴数为“2（C）”组也长于“4（E）”组。从该实验可以看出用药剂量为隔日 3 滴的重组人肿瘤坏死因子有助于加快创面愈合。

[1] Hu LP. Application of statistics triple-type theory in the experiment design. Beijing: People’s Military Medical Press, 2006:71-76. (in Chinese)

胡良平. 统计学三型理论在实验设计中的应用. 北京: 人民军医出版社, 2006:71-76.

[2] Hu LP. The practical course in the statistical analysis for windows SAS, version 6.12 & 8.0. Beijing: Press of Military Medical Sciences, 2001:203-206. (in Chinese)

胡良平. Windows SAS 6.12 & 8.0实用统计分析教程. 北京: 军事医学科学出版社, 2001:203-206.

[3] Graybiel A, Lackner JR. A sudden-stop vestibulovisual test for rapid assessment of motion sickness manifestations. Aviat Space Environ Med, 1980, 51(1):21-23.

胡良平，Email：lphu812@sina.com

10.3969/cmba.j.issn.1673-713X.2010.02.016