关于图的Grundy着色

徐保根

(华东交通大学基础科学学院,江西南昌330013)

1 定义及引理

本文所指的图均为无向简单图,文中未说明的符号、术语同于文献[1]。

设G=(V,E)为一个图,若 u∈V(G)则 NG(u)表示 u点在G中的邻域,d(u)=NG(u)为u点在G中的度。若S⊆V(G)则G[S]表示S在G中的导出子图。若u∈V(G)则G-u=G[V{u}]。若M⊆V(G),则 G-M=G[VM]。G表示G的补图,Pn、Cn和Kn分别表示n阶路、n阶圈和n阶完全图。

若G和H为两个点不交的图,则用G+H表示图G与H的直和图,即在G∪H中将图G的每个顶点与图H的所有顶点连接而成的图。

定义1.1[1]设G=(V,E)为一个图,一个函数被称为图G的一个真k-着色函数,如果对任意uv∈E(G)均有f(u)≠f(v)。图G的(点)色数定义为χ(G)=min{k 存在图G的真k-着色函数}。

近些年来,随着离散型事物的数学模型应用性的日益广泛,图的着色问题已不再是仅限于对图的点着色、边着色及全着色问题,各式各样的特征着色概念相继产生,如均匀着色、List着色等,从而使图的着色理论研究内容越来越丰富。Christen C A[2]等人引入了如下Grundy着色概念:

定义1.2[2]对于一个图G=(V,E),一个函数f:V→ 1,2,…,k如果满足条件:

(1)对G中任意相邻的两个点u和v,均有f(u)≠f(v);

(2)对任意两个整数 i和j(1≤i≤j≤k),若f(u)=j,则 NG(u)中必有一点 v,使得 f(v)=i,则称函数f为图G的一个Grundy k-着色函数。图G的Grundy色数定义为 Γ(G)=max{k｜存在图G的Grundy k-着色函数}。

由上述定义不难看出:Γ(G)≥χ(G)对任意图G成立,且对不任意两个点不交的图 G和H,均有 Γ(G∪H)=max Γ(G),Γ(H),因此本文中我们只考虑连通图。

引理1.3[3]对于任意图 G,若 v∈V(G)则 Γ(G-v)≥Γ(G)-1。

引理1.4 对于任意图 G,若 Δ=Δ(G)为图G的最大度,则 Γ(G)≤Δ+1。

证明:由定义1.2知,存在图G的一个Grundy Γ(G)-着色函数f及u∈V(G),使得 f(u)=Γ(G),从而对于每个

在NG(u)中必有vi使得f(vi)=i,即有

引理1.4证毕。

引理1.5[3]对于任意图G,均有

Zaker M[3]研究了二部图补图的Grundy色数,并探讨了一个图与其补图的Grundy色数的关系。在本文中我们主要给出图的Grundy色数的上界,并确定几类特殊图的Grundy色数。

2 Grundy色数的上界

我们首先分别给一般图、树和二部图的Grundy色数的上界。

证明:设 Γ(G)=k,f为图G的一个真Grundy k-着色函数。令,显然 Vi≠φ(i=1,2,…,k)。当1≤i≤j≤k时,记 E且由定义知 aij≥1,从而有

定理2.2 对于任意 n阶树T,均有 Γ(T)≤1+log2n

当1≤Γ(T)≤3时,由于1≤Γ(T)≤2时命题显然成立。而且3阶树只有 P3,且 Γ(P3)=2,因此,当Γ(T)=3时命题成立。

假若命题对于任何满足 Γ(T0)≤k-1(k≥4)的树 T0均成立,即有:若存在 T0的一个真Grundy j-着色函数(j≤k-1),则

现考虑任意一棵满足 Γ(T)=k的树T,f为T的一个真Grundy k-着色函数。

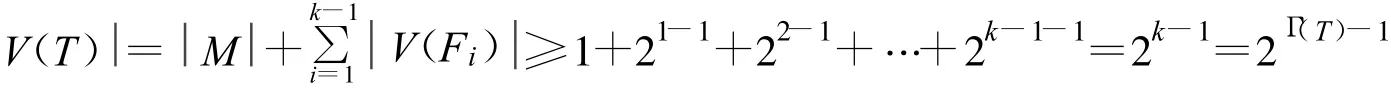
即命题对于任何满足 Γ(T)=k的树T也成立。由归纳原理,定理2.2证毕。

证明:设G=(V1∪V2,E)为一个二部图,Γ(G)=k,f为图G的一个真Grundy k-着色函数。由定义知:存在u∈V(G)使得 f(u)=k。不妨设 u∈V1,由于,注意到G为二部图,NG(u)⊆V2,即有由定义知:存在 v∈V2使得 f(v)=k-1,从而存在 k-2个点 ui∈V1使得f(ui)=i(i=1,2,…,k-2),注意到 u∈ V1且 u≠ui,因此

下面证明此上界是最好可能的。对n为奇数和偶数分别构造二部图如下:

当 n=2或3时,显然有二部图K1,1和K1,2,且 Γ(K1,1)=Γ(K1,2)=2。下面设 n≥4。

(1)当n=2k(k≥2)为偶数时,令G=(V1∪V2,E)为一个完全二部图Kk,k去掉k-1条独立边所得的图。记,所去掉k-1条独立边为 uivi(i=1,2,…,k-1)。定义图G的一个真Grundy k+1-着色函数f如下:

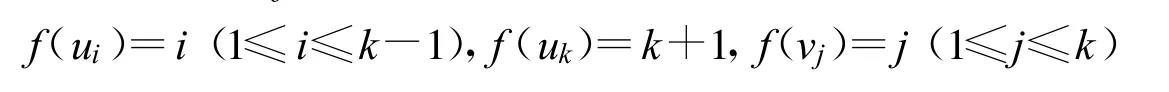
(2)n=2k+1(k≥2)为奇数时,在上述定义的图G中增加一个新顶点w,并将w点邻接V2中的所有顶点,所得的图记为G0。定义G0的一个真Grundy k+1-着色函数f0如下:

f0(w)=k+1,当v≠w时f0(v)=f(v),这里 f的定义同(1)。由此可见

定理2.4 对于任意两个点不交的图G和H,均有 Γ(G+H)≥Γ(G)+Γ(H)

证明:设 Γ(G)=k1,Γ(H)=k2,f1和 f2分别为图 G和图H 的真Grundy k1和k2-着色函数,定义 G+H的一个Grundy k1+k2-着色函数f如下:

不难验证:f为图G+H的一个Grundy k1+k2-着色函数,因此 Γ(G+H)≥Γ(G)+Γ(H)。定理2.4证毕。

定理2.5 设 n阶图G的度序列为d1≥d2≥d3≥…≥dn,则有

证明:设 Γ(G)=k,用dG(v)表示 v点在G中的度数。

(反证)假设存在某个 j(1≤j≤n)使得 Γ(G)=k≥dj+j+1。

证明:设 n阶图G的度序列为d1≥d2≥d3≥…≥dn,由定理2.5知:对每个 i(1≤i≤n),均有 Γ(G)≤di+i,从而有推论2.6证毕。

3 特殊图的Grundy色数

下面探讨几类特殊图的Grundy色数;

定理3.1 设Pn、Cn和Wn分别表示n阶路、圈和轮图,则有

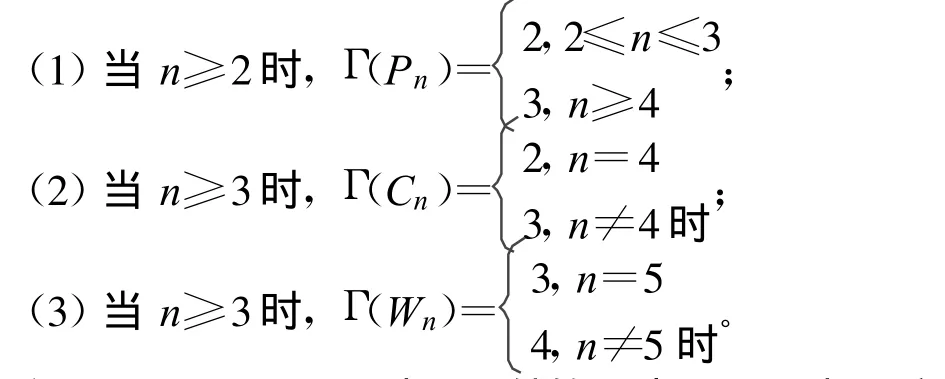
证明:(1)n=2,3时是显然的。当 n≥4时,一方面,由引理1.4知 Γ(Pn)≤3。另一方面,可定义Pn的一个真Grundy 3-着色函数f如下:记(j≥4)。由此可见:当 n≥4时,Γ(Pn)=3。

(2)n=3,4时是显然的。当 n≥5时,一方面,由引理1.4知 Γ(Cn)≤3。另一方面:当n为奇数时,可同(1)中一样地定义Cn的一个真Grundy 3-着色函数。

当 n为偶数时,记 Cn=(v1v2v3v4…vn)。定义 f如下:

不难验证:f为Cn的一个真Grundy 3-着色函数,即当n≥5时,Γ(Cn)=3。

(3)根据(2)及引理1.5即得,定理3.1证毕。

定理3.2 对任意完全 t-部图K(m1,m2,…,mt),均有 Γ(K(m1,m2,…,mt))=t

证明:令 G=K(m1,m2,…,mt),V(G)=V1∪V2∪…∪Vt,其中一方面,显然有 Γ(G)≥χ(G)=t。

另一方面,假若 Γ(G)=k≥t+1,由定义知:存在 G的一个真Grundy k-着色函数f及一点u∈V(G),使得 f(u)=k,从而在 NG(u)中必有 k-1≥t个顶点ui(1≤i≤k-1),使得 f(ui)=i。而 NG(u)中点至多在t-1部顶点集中,故必有某个Vs包含ui和vj(1≤i≤k-1)。由定义知:NG(uj)中必有某个顶点v使得f(v)=i=f(ui),注意到v∉Vs,从而 uiv∈E(G),这与 f的定义矛盾。定理3.2证毕。

[1]BONDY J A,MURTY V S R.Graph Theory with Applications[M].Amsterdam:Elsevier,1976.

[2]CHRISTEN C A,SELKOW S M.Some perfect coloring properties of graphs[J].J.Combin.Theory Ser.B,1979,27(1):49-59.

[3]ZAKER M.Results on the Grundy chromatic number of graphs[J].Discrete Math.,2006,306:3 166-3 173.