量子理论中一个定理的随机推广
2010-06-29欧谦宁
欧谦宁
(镇江机电高等职业技术学校,江苏镇江212016)
1 引言
量子化问题起源于信息理论和工程技术,历史可以追溯到20世纪40年代[1].最早最熟悉的有量子频标,半导体(包括你正在用来读这些文字的电脑、手机等),激光,核反应,甚至一般研究用的一些技术(算半个工程吧)像光谱分析,核磁共振,也包括顺磁共振,还有探针显微术系列(STM(扫描隧道显微镜),AFM(原子力显微镜)等).还有上届的诺贝尔奖、用在磁盘上的巨磁电阻效应,CPU就是典型的应用.另外量子信息(包括量子计算和量子通信)也在研究当中.
Graf和Luschgy系统地研究了这个问题并给出了具体的数学处理方法.由于自然现象的变化多端和不确定性,因此对随机性的研究将具有更广泛的实际意义.随着近几年随机分形研究的兴起,随机情况下量子理论也得到了广泛重视.主要研究量子理论中的一个定理在随机情况下也成立,这将进一步丰富量子理论.
2 基本概念
量子化理论的两个重要内容是量子化系数和量子化维数.
设μ是Rd上的一概率测度,0<r<∞,μ的r级n维量子误差定义为
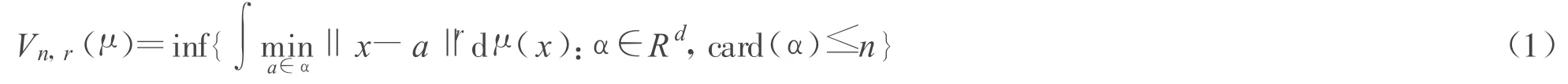
(card表示集合的基数)
如果式(1)中的最小值在某一确定的α∈Rd且card(α)≤n处取得,则称α为一个μ的r级n维量子误差的最优集.所有这些最优集组成的集类记作Cn,r(μ).μ的r级n维量子误差的上、下量子化维数定义为:
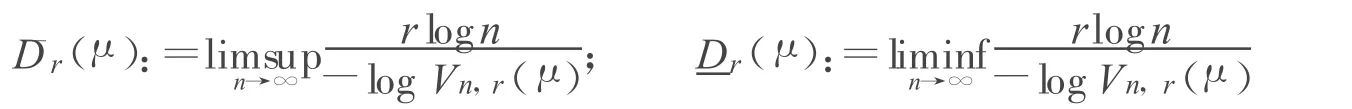
设{f1,…,fN}是Rd上压缩比为c1,…,cN的一列迭代相似函数系统,E为相应的唯一非空不变集,满足E.与迭代函数系{f1,…,fN}和给定概率(p1,…,pN)相关联的自相似测度 μ满足.称{f1,…,fN}满足强分离条件(SSC):如果 fi(E),1≤i≤N 两两不交.称{f1,…,fN}满足开集条件(OSC):如果存在一非空开集U 使得对所有i=1,2,…,N有fi(U)⊂U,且对任意 i,j,1≤i≠j≤N,fi(U)∩fj(U)=φ.在开集条件下Graf和Luschgy[2,3]证明了 μ的量化维数存在且等于Dr.其中Dr为下面方程的解:
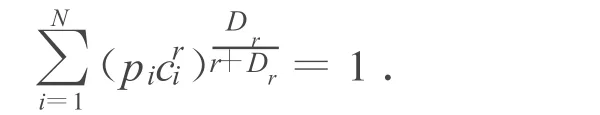
设(Ω,F,P)是一完备的概率空间,N是为一自然数且N≥2.设 Ξ:={1,2,…,N}是一指标集,Ξk:={(i1,i2,…,ik):ij∈ Ξ,1≤j≤k},
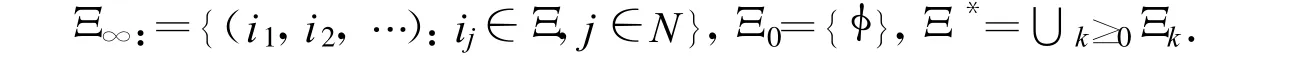
σ=(σ1,…,σk)∈ Ξk,称 σ的长度为k,记作|σ|=k.对任意 σ∈ Ξ*∪ Ξ∞且|σ|≥k,记 σ|k=(σ1,…,σk).如果 σ,τ∈ Ξ*且|σ|≤|τ|,σ=τ||σ|则称 σ为τ的前缀,记作 σ≺τ.如果既不是 σ≺τ也不是 τ≺σ,则称 σ,τ不可比较.一个有限集Γ⊂Ξ*称为有限对抗链,如果有Γ中任两个指标σ,τ都不可比较.一个有限对抗链Γ称为最大有限对抗链,如果对任一指标 σ∈ Ξ∞在 Γ中都有前缀.对 k≥2,σ=(σ1,…,σk)∈ Ξk,i∈ Ξ,定义
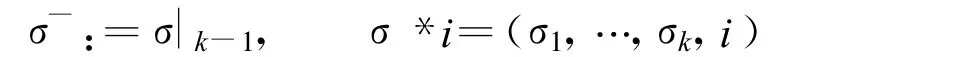
定义 1[4,5]: 设{f1,f2,…,fN}⊂con(Ω,E),K(ω,ω1,…,ωN)∈ M(ΩN+1,K(ε))称 K(ω,ω1,…,ωN)是一随机自相似集(R.S.S.S.):若存在一个集合 Ω0,p(Ω0)=1使得对所有(ω,ω1,…,ωN)∈ Ω有K(ω,ω1,…,ωN)=表示压缩映射集)
一般记 K(ω,ω1,…,ωN)=K(ω)
设
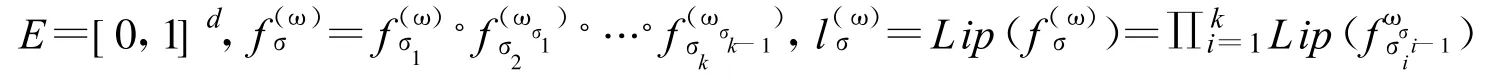
Eσ=fσ(E).EN+1为 PN+1的期望算子 .
与概率向量(p1,p2,…,pN)关联的随机自相似测度μ定义如下:
{
f1,f2,…,fN}⊂con(Ω,E)是Rd到Rd上的压缩因子为Lip(fi)(i∈Ξ)的相似映射.其分布为(p1,p2,…,pN)
则
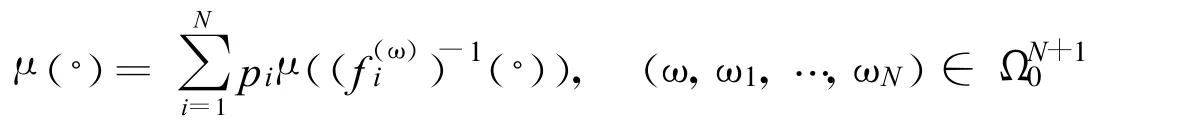
则K(ω)=suppμ是(f1,f2,…,fN)的吸引子.(supp为测度的支撑)
在文中,给出下面的定义和符号.对于 σ∈ Ξk,记显然序列是单调的.所以当k→∞时以概率1收敛到随机变量且有

设(A)ε为集A的ε一领域.由SSC,存在一常数 β>0使得对任一 σ∈ Ξk,有

对于 α∈Cm,r(μ)和 σ∈Γn,定义
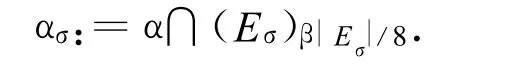
3 主要结论

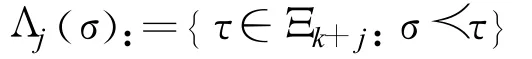

则由三角不等式得:
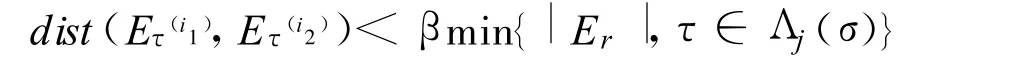
这与式(3)矛盾.因此,对每个 a∈ α,最多只有一个柱集 Eτ,τ∈ Λj(σ)使得式(4)成立.另一方面,由因此,存在某些使得
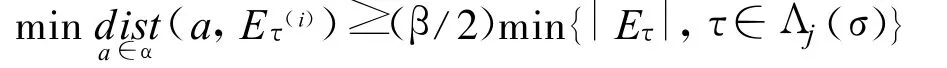
所以,得到
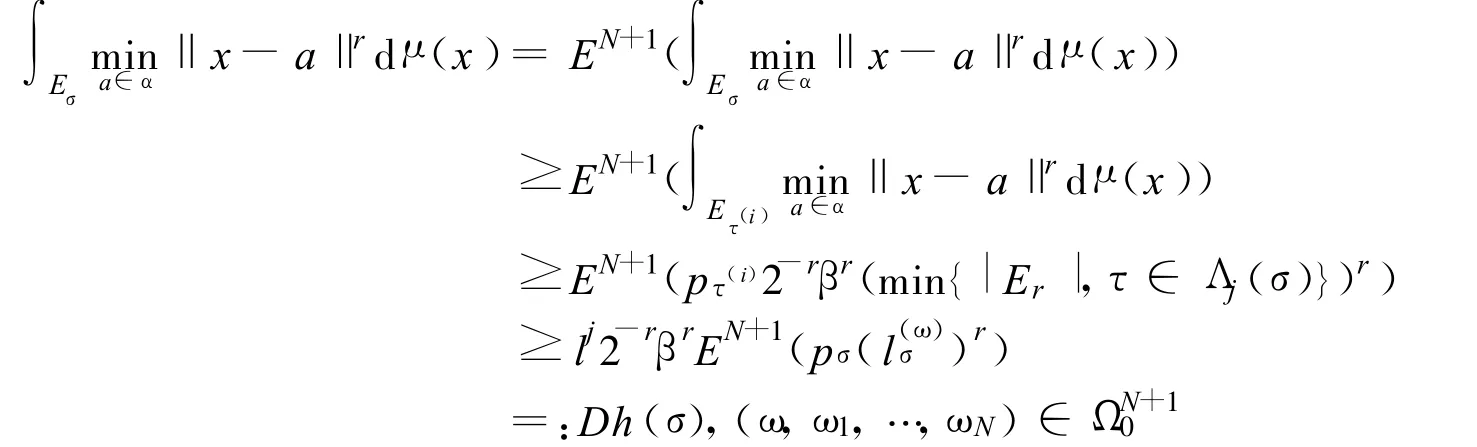
这里 D=lj2-rβr. 定理成立.
[1]J A Bucklew,G L Wise.Multidimensional asymptotic quantization with rth power distortion measures[J].IEEE T rans.Inform.Theory,1982,28:239-247.
[2]S Graf,H Luschgy.The quantization dimension of self-similar probabilities[J].Math.Nachr.,2002,241:103-109.
[3]S Graf,H Luschgy.The quantization of the Cantor distribution[J].Math.Nachr.,1997,183:113-133.
[4]D H Hu,X M Zhang.The random shift set and random sub-self-similar set[J].Acta Mathematica Sci-entia,2007,(2):267-273.
[5]D H Hu,X M Zhang.The Dimension for random sub-Self-Similar set[J].Acta Mathematica Scientia,2007,(3):561-573.
