亚纯函数微分多项式的一个正规定则
2010-06-29张兆迎鲍文竹
张兆迎, 鲍文竹
(成都信息工程学院数学学院,四川成都610225)
1 引言及结果
扈培础等在文献[1]中得到了下述结果:
定理A 设n,k≥2为正整数,a为有穷非零复数,F为区域D上的亚纯函数族,F中任一函数的零点重级至少为k.如果∀f,g∈F,f(f(k))n与g(g(k))nIM分担a,则F在区域D上正规.
定理B 设n,k为正整数,且n≥2,a为有穷非零复数,F为区域D上的亚纯函数族,F中任一函数的零点重级至少为k,且f(f(k)(z))n=a⇒|f(k)(z)|≤A,其中 A为正数,则F在区域D上正规.设L(f)=f(k)+a1f(k-1)+…+akf,a1,…,ak为常数.
将f(k)推广为微分多项式L(f),得到了下述结果.
定理1 设n,k≥2为正整数,a为有穷非零复数,F为区域D上的亚纯函数族,F中任一函数的零点重级至少为k.∀f,g∈F,fLn(f)与gLn(g)IM分担a,则F在D上正规.
定理2 设n,k为正整数,且n≥2,a为有穷非零复数,F为区域D上的亚纯函数族,F中任一函数的零点重级至少为k,且fLn(f(z))=a⇒|f(k)(z)|≤A,其中A为正数,则F在区域D上正规.
由定理1及定理2可得如下推论.
推论1 设n,k为正整数,且n≥2,a为有穷非零复数,F为区域D上的亚纯函数族,F中任一函数的零点重级至少为k,如果∀f∈F,fLn(f)≠a,则F在区域D 上正规.
2 几个引理
设区域D⊂C,F为区域D上的亚纯函数族,称 F在区域D上是正规的,如果任一{fn}⊂F有一个子列{fnj}在D上按球距内闭一致收敛于一个亚纯函数或∞.
引理1[2]设k是一个正整数,F是单位圆盘Δ上的亚纯函数族,F中任一函数的零点重级至少为k,如果F在z=0处不正规,则对于任一 α,0≤α≤k,存在:(1){zn}⊂Δ,zn→0;(2){fn}⊂F;(3)正数列{ρn},ρn→0(n→∞);使得gn(ζ)=ρ-αnfn(zn+ρnζ)在复平面上按球距内闭一致收敛于一个非常数亚纯函数g(ζ),并且g(ζ)的零点重级至少为 k,g#(ζ)≤g#(0)=1,g(ζ)的级至多为2.
引理2[1]设n,k≥2为正整数,a为有穷非零复数,如果f为复平面上的一个非常数亚纯函数,零点重级至少为k,则 f(f(k))n-a至少有两个判别的零点.
引理3[1]设n≥2为正整数,a为有穷非零复数,如果f为复平面上的一个非常数亚纯函数,则 f(f′)n-a至少有一个零点.
3 定理证明
定理1的证明:
若F在D上不正规.不失一般性,设F为单位圆盘Δ={z∈C:|z|<1}上的亚纯函数族且在原点z=0处不正规.由引理1知,存在点列{zj}⊂Δ且 zj→0(j→∞),函数列{fn}⊂F,正数列{ρn},ρn→0,使得 gj(ζ)=在复平面上按球距内闭一致收敛一个非常数亚纯函数g(ζ),并且g(ζ)的零点重级至少为 k,g(ζ)的级至多为2.
因此
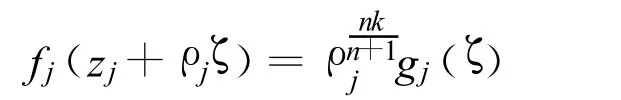
对ζ求导有

所以经过简单的计算

由于 ρj→0(j→∞)知,在复平面上除去 g(ζ)的极点外,
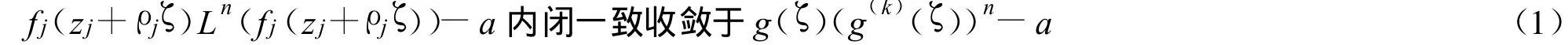
若g(ζ)(g(k)(ζ))n≡a,则g既无零点又无极点,又因g为一个级至多为2的非常数亚纯函数,所以存在常数ci(i=0,1,2)使得(c1,c2)≠(0,0),g(ζ)=ec0+c1ζ+c2ζ2,显然 g(ζ)(g(k)(ζ))n不恒等于a,矛盾.所以 g(ζ)(g(k)(ζ))n不恒等于a.
由引理 2,函数g(ζ)(g(k)(ζ))n-a至少有两个判别的零点,设其中两个为 ζ0,ζ*0.取适当小的 δ0>0,使得 B(ζ0,δ0)∩B(ζ*0,δ0)=Ø 且在B(ζ0,δ0)∪B(ζ*0,δ0)上除去 ζ0,ζ*0外没有其他零点,这里 B(ζ0,δ0)={ζ||ζ-ζ0|<δ0},B(ζ*0,δ0)={ζ||ζ-ζ*0|<δ0}.
由式(1)及Hurwitz定理知,当 j充分大时,存在点 ζj∈B(ζ0,δ0),ζ*
j ∈ B(ζ0*,δ0)使得
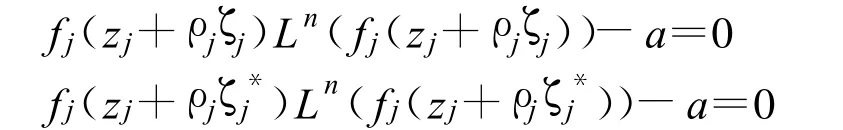
由假设f1Ln(f1)和 fjLn(fj)IM分担a知,
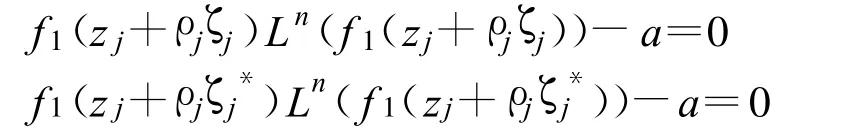
由非常数亚纯函数零点孤立性,f1Ln(f1)≡a.
同理∀f∈F,fLn(f)≡a.而矛盾 .
定理1证毕.
定理2的证明:
应用定理1证明过程中的符号记法.由Hurwitz定理知g(ζ)的零点重数至少为k,由引理2,引理3知g(ζ)(g(k)(ζ))n-a 至少有一个零点ζ0,所以 g(ζ0)≠∞.因此由 Hurwitz定理 ,存在{ζj},ζj→ζ0,使得 fj(zj+ρjζj)Ln(fj(zj+ρjζj))=a,由假设知,其中 A 为正数.
因此
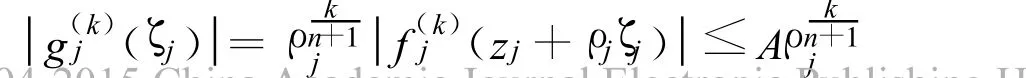
定理2证毕.
[1]Hu Pei-Chu,Meng Da-Wei.Normality criteria of meromorphic functions with multiple zeros[J].J.Math.Anal.Appl.,2009,357:323-329.
[2]L Zalcman.Normal familes:New perspectives[J].Bull.Amer.Math.Soc.,1998,35 :215-230.
[3]Y X Gu,X C Pang,M L Fang.Normal Families and Its Application[M].Beijing:Science Press,2007.
