无限群p拟Frattini子群

徐 威, 张志让

(成都信息工程学院数学学院,四川成都610225)

1 引言

对任意群G,它的Frattini子群定义为 G中极大子群的交,当G中不存在极大子群的时候,G的Frattini子群就是G本身[1]。此后又不少作者对多种类型的广义Frattini子群做了研究[2-5],在文献[6]中,J.B.Riles讨论了无限群的拟Frattini子群,在文献[7]中吕智颖等人研究了π拟Frattini子群。文中介绍一种新的拟Frattini子群——p拟Frattini子群,将给出这种子群的定义,并研究其基本性质。

设H是G的一个子群,则 H在G中的指数|G∶H|可能为1,素数,合数或者∞。为了方便起见,如果|G∶H|为合数或者∞,那么,简称|G∶H|为非素数。

在第2节中,给出与p拟Frattini子群相关的一些基本定义。

在第3节中,将讨论一些关于p拟Frattini子群的基本性质。

在第4节中,研究正规子群,同态像和直积的拟Frattini子群,同时,简单地介绍子群 G的p拟补充和p拟补,对它们作初步的研究。

2 基本定义

本节中,介绍几个基本定义。

定义1 设 x是群G的元素,如果存在G的某一子集S,使得|G：＜S＞|是非素数,但|G：＜x,S＞|是1或者素数,那么称x是G的p拟生成元。于是,如果对于任意具有性质|G：＜x,S＞|是1或者素数的 G的子集S,都有|G：＜S＞|也是1或者素数,那么称 x为G的p拟非生成元。

引理1 设 x和y是G的p拟非生成元,则 xy-1和 xα也是p拟非生成元,其中,α是G的自同构。

证明：设 S⊆G 且|G：＜xy-1,S＞|是1或者素数,则|G：＜xy-1,y,S＞|也是1或者素数,从而

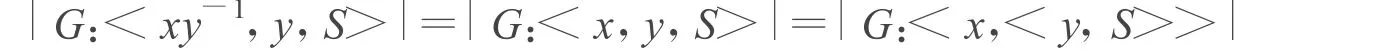
因为 x和y都是G的p拟非生成元,所以|G：＜S＞|是1或者素数,从而 xy-1是 G的p拟非生成元。同理,可证得xα也是p拟非生成元。证毕。

因此,G的所有p拟非生成元所构成的集合pU(G)是G的特征子群,称为下p拟Frattini子群。

定义2 如果|G：M|是非素数,但对于任意 M＜N≤G,都有|G：N|是 1或者素数,那么 M称为G的p拟极大子群。G的所有p拟极大子群的交pV(G)称为 G的上p拟Frattini子群。如果G中没有p拟极大子群,那么G的上p拟Frattini子群就是G本身,即pV(G)=G。

这里要说明,上述定义中涉及的素数指的是任意素数,但在文献[7]中相关定义中 π是指某一个固定素数的集合,这两者有很大的区别。

引理2 对于任意群G,pU(G)≤pV(G)。

证明：对于任意不属于pV(G)的元素x,都存在一个p拟极大子群M,使得x∈/M,|G：M|是非素数,但|G：＜x,M＞|是1或者素数,也就是说x是G的p拟生成元,即x∈/pU(G)。故pU(G)≤pV(G)。证毕。

定义3 设pU(G)和pV(G)分别是G的下p拟Frattini子群和上p拟Frattini子群。当pU(G)=pV(G)时,这个子群称为 G的p拟Frattini子群,记为pφ(G)。

若F是有限群,则pU(F)=pV(F)=pφ(F)。但是一般来说对于任意群 G,pU(G)和pV(G)不一定相等。但对于下面的较广泛的群类来说,这两个特征子群是一致的。因此引入如下定义：

定义4 如果对于 G的满足|G：H|是非素数的子群 H,一定存在G的一个p拟极大子群M,使得H≤M,那么称群G为pF群。

引理3 设群 G为pF群,则pV(G)=pU(G)。

证明：显然有pU(G)≤pV(G);只需证pV(G)≤pU(G)。如果对任意 x∈/pU(G),即存在 G的子集S,使得|G：＜S＞|是非素数,但|G：＜x,S＞|是1或者素数。由于群G为pF群,因此存在 G的p拟极大子群M,使得＜S＞≤M。由于＜x,S＞≤＜x,M＞且|G：＜x,S＞|是1或者素数,因此|G：＜x,M＞|也是1或者素数。又由定义|G：＜M＞|是非素数,所以 x∈/M 。故 x∈/pV(G)。证毕。

定理1 设G是有限生成群,那么 G是pF群。

证明：设H是G的子群,使得|G：H|是非素数。假设B1≤B2≤…≤Bi≤…是具有下列性质的子群组成的升链：|G：B|是非素数,H≤Bi。令B=∪iBi,若|G：B|是1或者素数,由于 G是有限生成的,所以 B也是有限生成的[8]。因此存在 i0,使得B=Bi0,但|G：B|是非素数,这就与 Bi0的选择矛盾。所以|G：B|是非素数,显然知B≥H。由左恩(Zorn)引理知,一定存在极大的满足上述性质的子群 M。对任意满足 M＜N≤G的子群N,显然有 N≥H,如果|G：N|是非素数,则与M 的极大性矛盾。故|G：N|是1或者素数,由p拟极大子群的定义知,M是G的p拟极大子群。即对任意H≤G,|G：H|是非素数,都有G的p拟极大子群M,使得 H≤M,故 G是pF群。证毕。

由定理1和引理3可知,在有限生成的群 G中一定有pV(G)=pU(G);等价地,有“如果pV(G)≠pU(G)成立,那么G一定是无限生成的”。当然必须指出,群 G的无限生成性只是pV(G)≠pU(G)成立的必要条件,并不是充分条件。举两个例子来说明当群是无限生成时,仍然可能有pV(G)=pU(G)。

例1.设G是无限初等Abelp-群,那么pV(G)=pU(G)=1。

证明：设M是G的任一p拟极大子群,由初等Abelp-群的性质知|G：M|=pn。从而G的所有p拟极大子群的交pV(G)等于1。但是由引理2,pU(G)≤pV(G),从而也有pU(G)=1=pV(G)。显然G是无限生成的。证毕。

例2.设群G是关于素数p的拟循环群,那么pV(G)=pU(G)=G。

证明：首先证明,在群 G中G的p拟非生成元即为G的非生成元。设 x是G的p拟生成元,由定义可知,对于任意具有性质|G：＜x,S＞|是1或者素数p的G的子集S,都有|G：＜S＞|也是1或者素数p。但是拟循环群的真子群均为有限群,即G的真子群在G中的指数无限,所以,可从|G：＜x,S＞|是1,即G=＜x,S＞得到G=＜S＞,故 x为G的非生成元。因为G的Frattini子群Frat(G)正好是G的非生成元的集合,故Frat(G)=pU(G)。但是也由拟循环群的真子群为有限群,故G没有极大子群,即Frat(G)=G,从而pU(G)=G。也由引理2 pV(G)≥pU(G),故pV(G)=G=pU(G),显然G是无限生成的。证毕。

3 p拟Frattini子群的基本性质

在这一节中,讨论类似于Frattini子群的性质的p拟Frattini子群的基本性质。

定义5 由群G中的元素所构成的子集合S称为G中p拟生成元的既约集,如果满足如下条件：如果|G：＜S＞|是1或者素数,但对于每一个S的真子集T,都有|G：＜T＞|是非素数。把那些不属于G的任意一个p拟生成元的既约集的元素所构成的集合记为pW(G)。

显然,对于任意群 G,有pU(G)≤pW(G)。

引理4 如果G是有限生成,那么 G的每一个p拟生成元的既约子集S也是有限的。如果存在G的子群T,使得|G：T|是1或者素数,那么T的每一个生成元的集合都包含G的一个p拟生成元的既约子集。

证明：由于G是有限生成的且|G：＜S＞|是有限的,故＜S＞是有限生成的。设＜S＞由 x1,…,xn生成,其中每一个 xi都可以写成S∪S-1中有限个元素的乘积的形式。因此,＜S＞由S的有限子集合生成的。这个有限子集不可能是S的真子集,这是因为S是G的p拟生成元的既约子集。所以S是一个有限集合。

由于G是有限生成的,并且|G：＜T＞|是有限的,T也是有限生成的。令 T是由t(1),…,t(m)生成的,按如下的办法构造{t(1),…,t(m)}的一个子集 T′：

逐次考虑每一个 t(i),按照由已保留的t(j)和t(i)后面的t(j)生成的子群在G中的指数是否为非素数决定保留和删去t(i)。当|G：＜t(2),…,t(m)＞|是非素数时,保留 t(1),否则就删去t(1);当 t(i1),…,t(ik)已被保留,若|G：＜t(i1),…,t(ik),t(ik+2),…,t(m)＞|是非素数,则保留 t(ik+1),否则就删去 t(ik+1)。依此类推,保留下来的元素构成的{t(1),…,t(m)}的子集合 T′,就是G的p拟生成元的既约子集。证毕。

定理2 如果 G满足极大条件,那么pφ(G)=pW(G)。

证明：由于G满足极大条件,所以G是pF群,于是有pφ(G)=pU(G)≤pW(G)。如果x∈/pφ(G),则存在G的子集S,使得|G：＜S＞|是非素数,但是|G：＜x,S＞|是 1或者素数,设＜S＞由 a1,…,an生成,那么|G：＜x,a1,…,an＞|是1或者素数。对{x,a1,…,an}应用引理 4中类似的方法,可以得到{x,a1,…,an}的一个子集Si,它包含x且为G的p拟生成元的既约集。因此x∈/pW(G)。综上有,pφ(G)=pW(G)。证毕。

定义6 设S是群G的子集。如果对于|G：＜S,T＞|是1或者素数的 G的子集T,都有|G：＜T＞|是1或者素数,那么S称为在G中是p拟可消的。

引理5 每一个p拟可消集的子集本身也是p拟可消的,并且G的p拟可消集包含在pU(G)中。

证明：令 S是p拟可消集,且 S′⊆S。假设存在 T⊆G且|G：＜S′,T＞|是1或者素数,那么|G：＜S,T＞|整除|G：＜S′,T＞|,因此|G：＜S,T＞|是 1或者素数。由于 S是p拟可消的,故|G：＜T＞|是1或者素数。从而S′是p拟可消的。设 x是p拟可消集合的任一元素,由{x}也是p拟可消集,因此 x是G的p拟非生成元,从而x∈pU(G)。证毕。

引理6 如果pφ(G)是有限生成的或者 G是pF群,那么pφ(G)是p拟可消的。

证明：设pφ(G)是有限生成的,它的生成元是 x1,…,xn。对每一个 xi,当 T⊆G且|G：＜xi,T＞|是1或者素数时,都有|G：＜T＞|是1或者素数。因此,如果|G：＜pφ(G),T＞|是 1或者素数,那么|G：＜T＞|也是1或者素数。于是pφ(G)是p拟可消的。

设 G是pF群,则有pU(G)=pφ(G)。假设存在 G 的子集T,使得|G：＜pφ(G),T ＞|是1或者素数,但|G：＜T＞|是非素数,那么存在p拟极大子群M,使得＜T＞≤M 。因此|G：＜pφ(G),M ＞|整除|G：＜pφ(G),T＞|也是1或者素数。但是 φ(G)≤M,故|G：＜pφ(G),M ＞|=|G：M|为非素数,矛盾!所以pφ(G)是p拟可消的。证毕。

引理7 设pφ(G)是 G 的p拟Frattini子群,如果pφ(G)是p拟可消的,那么 G 的正规子群N 包含在pφ(G)中的充分且必要条件是：如果H≤G且|G：NH|是1或者素数,那么|G：H|是1或者素数。

证明：假设 H≤G 且|G：NH|是1或者素数,那么有|G：H|是1或者素数。如果 N 不在pφ(G)=V(G)中,那么存在 G的p拟极大子群M,使得 N 不在M中,所以|G：NM|是1或者素数,但|G：M|是非素数,矛盾。故N ≤pφ(G)。证毕 。

反之,如果 N≤pφ(G),因为pφ(G)是p拟可消的,故由引理5知,N 本身也是p拟可消的。所以,若H≤G且当|G：NH|是1或者素数,那么总有|G：H|是1或者素数。证毕。

4 正规子群,同态像和直积的p拟Frattini子群

首先,介绍正规子群的p拟Frattini子群。

定理3 设 Y 和Z 是pF群,且 Z◁Y,又设 X ◁Y,使得 X ≤pφ(Z),那么 X ≤pφ(Y)。

证明：由引理6知,pφ(Y)是p拟可消的,因此,根据引理7,只需证明“如果 H≤Y是Y 的一个子群使得|Y：XH|是1或者素数,那么|Y：H|也是1或者素数”。

因为 XH ≤Z(XH)≤Y,|Z(XH)：XH|是 1或者素数,因此|Z：(XH)∩Z|=|Z：X(H ∩Z)|是1或者素数。又因为X ≤pφ(Z),故|Z：(H∩Z)|是1或者素数(根据引理 6),从而|X(H∩Z)：(H ∩Z)|是1或者素数。现在有 X(H ∩Z)H=XH 和(XH)∩Z∩H=H∩Z,因此|XH ：H|=|X(H ∩Z)H ：H|=|X(H ∩Z)：(XH)∩Z∩H|=|X(H∩Z)：H∩Z|是1或者素数。证毕。

应用定理3,可以得到两个很有用的结论。在定理3中,如果将其中的 Y,Z和X分别取为G,N和pφ(N),就得到了下面的结果：

推论1 如果 G和N◁G 都是群pF,那么pφ(N)≤pφ(G)。

推论2 如果 G是pF群,H是G的正规的素数阶子群,那么H≤pφ(G)。

这是因为如果 H是素数子群,那么它没有p拟极大子群,从而pφ(H)=H,因此 H≤pφ(G)。

接着考虑同态像的p拟Frattini子群。

设群 G 有p拟Frattini子群,如果 γ是G 到Gγ的一个同构,Gγ的p拟Frattini子群是pφ(Gγ),那么有pφ(G)γ≤pφ(Gγ)。这是因为 Gγ的每一个p拟极大子群都是G的p拟极大子群在γ下的像。特别地,有下面一个有用的性质：

定理 4 (i)设 G 有p拟 Frattini子群pφ(G),如果 N ◁G,有 N ≤pφ(G),并且pφ(G/N)存在,那么pφ(G/N)=pφ(G)/N 。

(ii)设 N ◁G,如果pφ(G)存在且pφ(G/N)=1,那么pφ(G)≤N 。

证明：(i)因为 N≤pφ(G),故对于 G的每一个p拟极大子群M,都有 N ≤M,从而pφ(G/N)=∩M/N=(∩M)/N=pφ(G)/N,因此pφ(G/N)=pφ(G)/N 。

(ii)由前面的讨论知道,pφ(G)N/N ≤pφ(G/N)。但是pφ(G/N)=1,故pφ(G)≤N 。证毕。在定理4中,如果取 N=pφ(G),就可以得到下面的结论：

推论 3 对任意群 G,如果pφ(G)和pφ(G/pφ(G))存在 ,pφ(G/pφ(G))恒等于1。下面给出关于群的直积的p拟Frattini子群的结论。

定理 5 如果 G 是pF群,并且 G=Dri∈IGi,那么pφ(G)=Dri∈Ipφ(Gi)。

证明：容易证明对每一个 i∈I,Gi是pF群。由推论1知,pφ(Gi)≤pφ(G)

因此 Dri∈Ipφ(Gi)≤pφ(G)。现在只需证 Dri∈Ipφ(Gi)≥pφ(G)。

假设在pφ(G)中存在一个元素g,g∈/Dri∈Ipφ(Gi)。由群的直积的性质,g=gλ1gλ2…gλ t,其中gλi∈Gi(i=1,2,…,t)。由于g∈/Dri∈Ipφ(Gλi),故至少存在指标λi,使得gλi∈/pφ(Gi),不失一般性,假设gλ1∈/pφ(Gλ1),那么有Gλ1的p拟极大子群Mλ1,使得gλ1∈/Mλ1。令J=Iλ1,那么M=(Drλ∈JGλ)×Mλi是G的p拟极大子群,并且g不属于M,从而g∈/pφ(G),矛盾。因此pφ(G)=Dri∈Ipφ(Gi)。证毕。

最后,讨论子群的p拟补充和p拟补。

定义7 (i)设N是G的正规子群,如果存在 G的子群H,使得|G：H|是非素数,但|G：NH|是1或者素数,那么N称为在G中可以p拟补充。H为G中N的p拟补充。

(ii)设 N是G的正规子群,若存在G的子群H,使得H是G中N的p拟补充,并且N∩HG=1,那么 N称为在G中可以p拟补。

根据p拟补的定义和引理7,很容易得到下面的结论：

定理6 设群 G的p拟Frattini子群pφ(G)是p拟可消的,那么G的正规子群N在G中可以p拟补充的当且仅当N ≤/pφ(G)。

[1]G.Frattini.Intorno alla generazione dei gruppi di operazioni[J].Atti aella Real Acdemic dei Lincei,Rerd.ser.4,1(1885)：281-285,455-456.

[2]李晓华.Frattini子群的一些推广[J].四川师范大学学报(自然科学版),2001,24(4)：349-352.

[3]L.-C.Kappe,J.Kirtland.Some analogues of the Frattini subgroup[J].Algebra Colloq.1997,4(4)：419-426.

[4]Zhirang Zhang.The intersection of maximal subgroups with finite index[J].SEA Bull.Math.Springer-Verlag,2006,30：1007-1008.

[5]Zhirang Zhang,Ying Wang.The intersection of maximal subgroups with index a π-number[J].四川师范大学学报(自然科学版),2007,30(6)：688-690.

[6]J.B.Riles,The near Frattini subgroups of infinite groups[J].J.Algebra 1969,12：155-171.

[7]Zhiying Lv,Zhirang Zhang,Guangwu Zhao.TheNear Frattini Subgroups of Infinite Groups[J].西南大学学报(自然科学版),2009,31(4)：1-5.

[8]D.J.S.Robinson.A Course in the Theory of Groups,2nd ed[M].New York：Springer-Verlag,1996.