商用飞机气象观测温度、风场随机误差分析
2010-06-29乔晓燕马舒庆陶士伟赵培涛官福顺
乔晓燕, 马舒庆, 陶士伟, 赵培涛, 官福顺
(中国气象科学研究院,北京100081)
1 引言
目前,商用飞机气象观测用AMDAR(Aircraft Meteorological Data Relay)来代指。AMDAR即航空器气象数据中继是飞机对地通讯系统的泛指,用来代表对现代商用飞机上进行的自动气象观测资料的收集系统。AMDAR是国际民航组织和世界气象组织积极推动的全球性的项目。我国于2001年底在中国气象局和中国民航总局的协商下启动了AMDAR项目,此后AMDAR报告的数量逐渐增加。并且开始逐步应用于气象预报以及机场临近预报业务。
AMDAR资料的质量好坏关系着其在天气预报业务中的应用效果,就这一点而言,研究AMDAR资料的质量是一项非常有意义的工作。目前,美国NOAA在这方面开展了大量的工作。例如1995年,通过与机场附近的探空资料对比分析了飞机气象资料的误差特性。1999年,选取满足一定时间间隔(不超过10min)和空间间隔(水平距离不超过10km、垂直距离不超过30m)的飞机观测要素数据对(数据对取自不同飞机)进行了对比研究,利用统计学方法计算出了飞机观测随机误差均方根。国内在这方面开展的工作较少,2006年国家气象中心利用统计学方法对北京54511站2005年7月早00:00时探空资料与同时间北京首都国际机场飞机起飞时的AMDAR数据分5个层次进行对比,各要素取月平均值。结果表明AMDAR资料和探空资料的差别很小。但是没有计算AMDAR资料和探空资料的差值,以及均方根误差。
AMDAR资料与探空资料对比时,两者要素差值的均方根包括来自AMDAR观测的误差和来自探空观测的误差,但无法从标准差中分离出AMDAR观测误差。借鉴1999年美国NOAA所用的分析方法,对北京首都国际机场2007年1-8月份飞机起降时的气象数据进行了研究,计算了不同飞机的AMDAR数据之间的差值以及该差值的均方根,并利用统计学方法估计了飞机观测的误差。
2 AMDAR气象观测
目前国内商业飞机上气象观测要素包括时间、高度(有气压换算得到)、经纬度、飞机飞行状态、气温、风向、风速。飞机在各个阶段的观测频次见表1。
飞机在降落阶段垂直分辨率大约在600m左右,在飞机起飞阶段垂直分辨率要好一些,在起飞阶段0-1400m数据空间密度最大。

表1 飞机各阶段观测频率
AMDAR气象要素观测原理为:
(1)气温观测:温度传感器探头观测值是大气总温,空气静温(自由气流的温度)与大气总温不同,由马赫数对大气总温修正得到空气静温,其表达式如下:
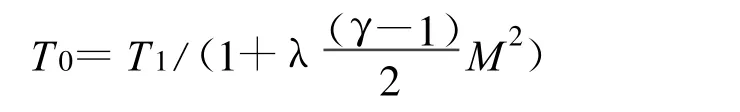
其中T0是大气静温、T1是大气总温、M 是马赫数。马赫数由空气总压和大气静压的计算得到,总压和静压均有皮托管测得。由此可知,气温观测误差源包括来自总温观测、总压观测、静压观测以及计算和订正误差。
(2)风速风向观测:风矢量的测量是非常复杂的。由飞机相对于地面的速度和飞机相对空气速度相减获得。利用从飞机导航系统(一般是惯性导航系统)和空速系统(一般是皮托管)获得的数据,加上从温度传感器获得的数据,可以计算出具有很高准确度的飞机相对于地面的速度 Vg和空气相对于飞机的速度Va,从而可计算出风速 V,表达式如下:
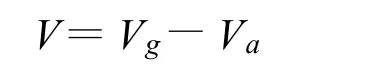
对于大多数应用,只测量风的水平分量。这时要求输入的数据缩减为只需空速、航向和地速。航向和地速取自导航系统,真空速需根据空速指示器的校正空速计算出来。水平风的分量(u,v)为:
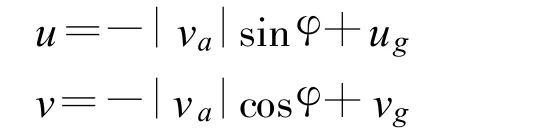
其中,|va|是真空速的绝对值,φ为相对正北的航向,ug和vg是地速的分量。
3 分析方法及资料获取
3.1 误差分析方法
首先利用统计学知识计算出数据对间要素差值的均方根 σ。假设:不同飞机的系统误差是一样的或没有系统误差;不同飞机的随机误差是相互独立的。则此均方根满足下面的公式
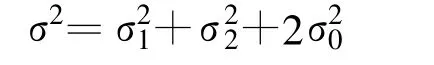
其中σ1、σ2分别代表两飞机的观测随机误差,σ0代表两飞机所处位置的中尺度过程引起的均方根误差。如果两飞机的时空间隔足够小,中尺度过程引起的均方根误差可以忽略。在大样本统计的情况下,可以认为两飞机的观测误差相同,则飞机随机误差为
3.2 AMDAR资料获取
研究数据是北京首都国际机场2007年1-8月飞机在航站起飞和降落的AMDAR数据。所选数据通过质量控制去除了含有粗大误差的数据点,所用数据仅包括飞机系统误差和观测随机误差。表2给出了温度观测随机误差随数据对时空间隔的变化情况。由表2可看出随着数据对时间间隔和空间间隔的变小,温度观测随机误差明显变小,也就是说随着时空间隔的减小,由于中尺度变化造成的随机误差减小。由此可以用时空间隔足够小的数据对来估计飞机气象观测随机误差。

表2 AMDAR温度资料观测误差均方根随样本数据对(来自不同飞机)时间间隔和水平间隔的变化
因此,选取数据对满足的条件设定为:时间间隔小于10min、水平间隔小于10km、垂直高度差不超过30m。该条件足以反映两飞机观测的随机误差,由于中尺度变化造成的误差已经很小。
4 结果分析
4.1 温度误差特性分析
表3给出温度观测随机误差在各层的情况。可以看出随着气压的降低(高度的增加)飞机观测随机误差总体趋势是下降的。在大气边界层温度观测误差均方根最大,可达0.91℃。在300hPa-500hPa层温度观测误差均方根最小,主要是由于对流层上层湍流运动减弱,由于湍流运动引起的气象要素的变化减小。

表3 各气压层的温度观测随机误差
数据对温度差值的分布也与温度本身有关(如图1)。由图1可见,在温度较高时温度差的分布比较离散,大差值较多。较低温度时大差值较少且越来越集中在较小值。温度小于-20℃时,其差不超过 2℃。温度大于 20℃时,其差可达6℃。
4.2 风矢量误差特性分析
风矢量误差特性分析中与温度相同,风速观测随机误差也随着气压的降低而减小。如表4所示,风速差观测随机误差在300hPa-500hPa气压层为最小值(1.03m/s)。因为在高层大气对流层,湍流运动引起的风速空间变化减小。在300hPa-500hPa气压层可以认为中尺度变化引起的误差达到最小值。
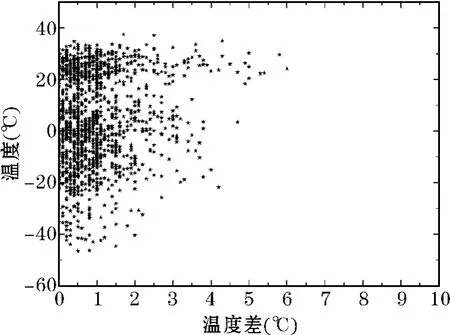
图1 温度差与平均温度关系
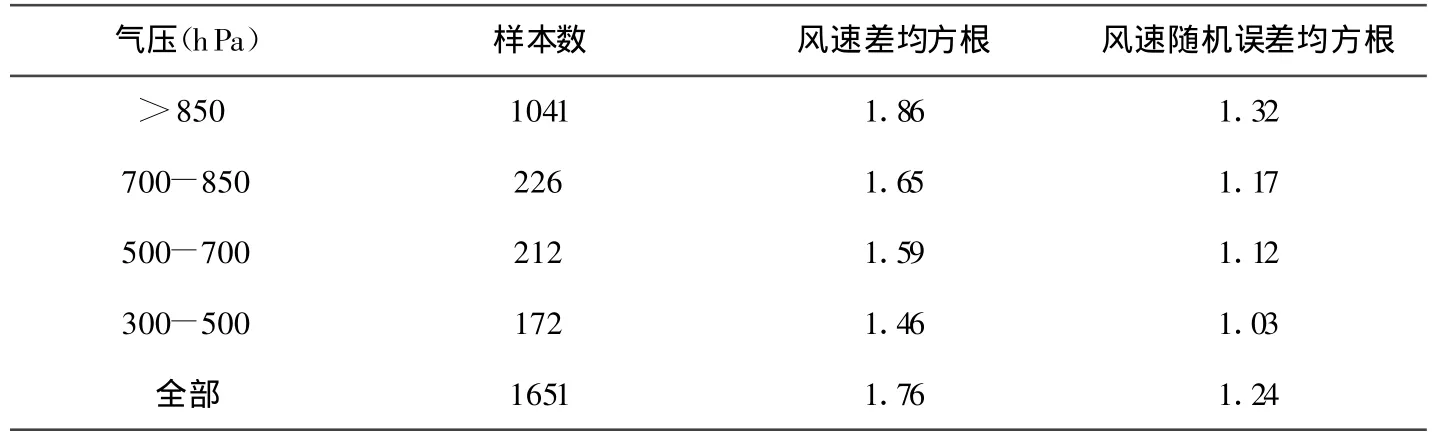
表4 各气压层风速观测随机误差
风速差的分布也与风速的大小有关。图2反映了风速差随风速的变化情况。所用的样本数为1651个,由于风速、风速差都是整数,很多点在图中重合在一起。总体趋势是:风速较大时风速差都较小,风速较小时会出现较大的风速差值。特别是风速大于30m/s时,风速差值不超过4m/s。
风向是比较难测量的要素,影响因素很多,所以风向差一般比较大,但是风向的测量精度与风速的大小也有关。图3给出了样本风向差随风速的变化,风速较小时风向差较大,当风速达到一定值时风向差较小。风速大于10m/s时,不同飞机测得的风向差值很小。
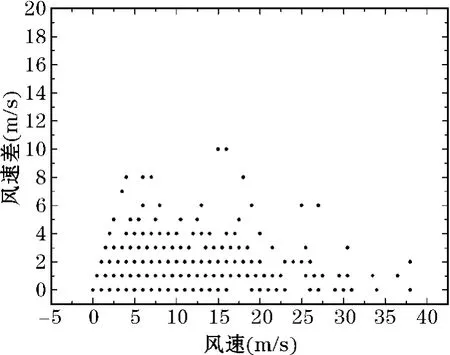
图2 风速差随风速的变化
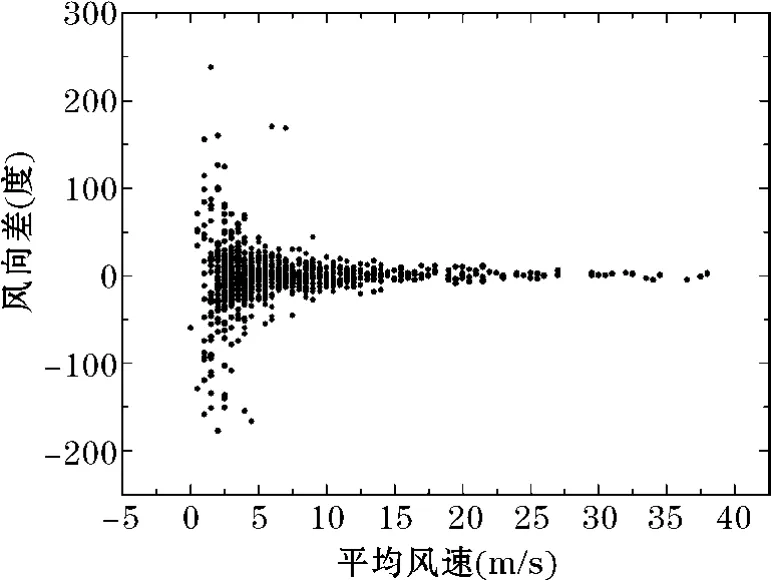
图3 风向差随风速的变化
5 与美国NOAA统计结果的对比
1999年美国NOAA对美国中部地区1996年8月-1997年8月的AMDAR数据进行了统计。所选数据对与本文相同:时间间隔小于10min、水平间隔小于10km、垂直高度差不超过30m。其结果如表5所示。对比表3和表5可知:我们的温度观测误差均方根略大于美国NOAA的统计结果,但差别不大,两温度观测随机误差随气压的变化趋势基本一致。对比表4和表5可以看出,我国的商用飞机风速观测随机误差小于美国NOAA统计的风速观测随机误差,两者随气压的变化趋势一致。由此可见:我国2007年1-8月份的飞机观测数据和美国1996年8月-1997年8月的飞机观测数据相比,温度观测资料随机误差相近,我国飞机风速观测随机误差要小于美国的。
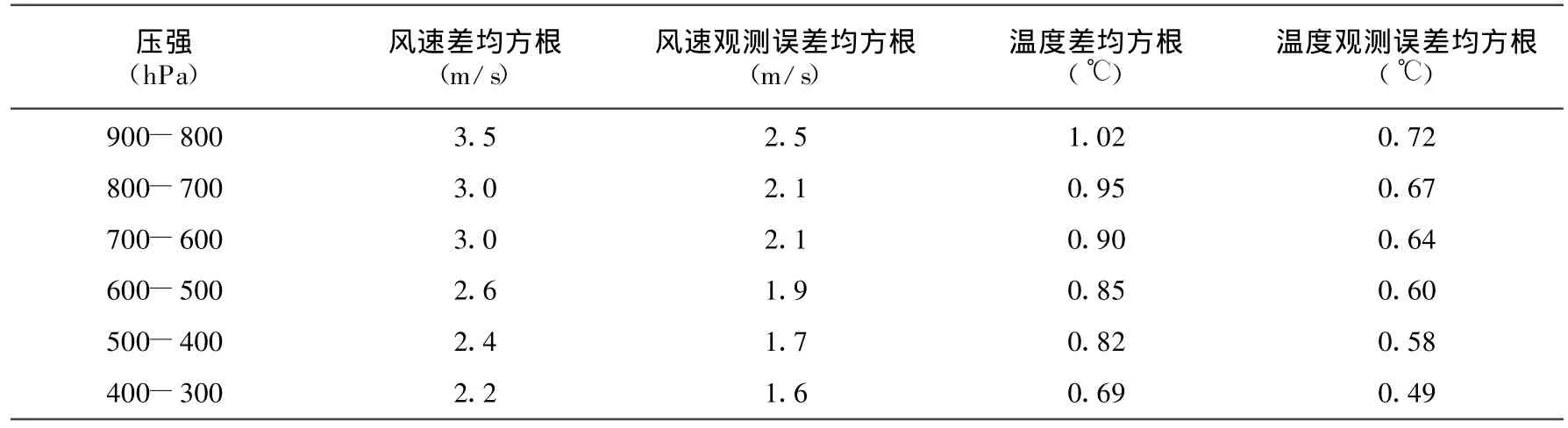
表5 美国NOAA统计结果
6 结论
通过选取满足一定时空间隔不同飞机观测数据并对每对观测风速差、风向差、温度差进行统计分析,揭示了商用飞机气象观测误差的一些特性,结论如下:
(1)温度观测随机误差、风速观测随机误差均随着气压的减小(即高度的增加)而变小。在对流层底部(>850hPa)时观测随机误差最大,温度观测随机误差均方根为0.90℃,风速观测随机误差均方根为1.24m/s。在300hPa-500hPa层温度观测误差均方根最小。与1999年美国NOAA统计结果相比,风速观测随机误差均方根在各气压层均比美国NOAA的统计结果要小一些,而温度观测随机误差均方根与美国NOAA的统计结果差别不大。
(2)温度观测误差与温度本身有关,温度较低时,温度差较小,精度较高。同样风速观测误差、风向观测误差也与风速有关,风速较大时,风向差、风速差均较小。风向差随风速的变化较明显,风速超过10m/s时,风向差都很小。
致谢:感谢中国气象局气象探测中心高空室给予的帮助!
[1]Stanley G Benjamin,Barry E Schwartz.Accuracy of ACARS Wind and Temperature Observations Determined by Collocation[J].Weather and Forecasting,1999,14:1032-1038.
[2]Barry Schwartz,Stanley G Benjamin.A Comparsion of Temperature and Wind Measurements from ACARS-E-quipped Aircraft and Rawinsondes[J].Weather and Forecasting,1995,10:528-543.
[3]Geneva Switzerland.Sensors and Measurements[M].AMDAR Reference Manual,2003.
[4]Fleming,R J.The use of commercial aircraft as platforms for environmental measurements[J].American meteorological society,1996,77:2229-2242.
[5]刘小魏,曹之玉,兰海波.AMDAR资料特征及质量分析[J].气象科技,2007,35(4):480-483.
[6]黄卓,李延香,王慧.AMDAR资料在天气预报中的应用[J].气象,2006,32(9):42-48.
[7]拓瑞芳,金山,丁叶凤.AMDAR资料在机场天气预报中的应用[J].气象,2006,32(3):44-48.
[8]贾朋群,胡英,王金星.民用航空气象观测综述[J].气象科技,2004,32(4):213-218.
