几种不同模型参数估计法的性能分析

2010-06-28聂建栋卫红凯

舰船电子对抗 2010年4期

聂建栋,卫红凯,李猛

(1.海军驻武汉438厂军事代表室,武汉430033;2.海军工程大学,武汉 430033;3.海军 704厂,青岛 266109)

0 引言

功率谱估计是利用给定的样本估计随机信号的功率谱密度,表征信号能量随频率的分布特性。最初的谱估计方法有周期图法和自相关法,称为经典功率谱估计法。周期图法假设观察数据区域外的数据为零,自相关法假设数据在延迟窗以外的自相关函数为零,2种方法均无法实现功率谱密度原始定义中的求均值和求极限的运算,使得其在功率谱估计中不仅方差性能较差,而且分辨率较低,难以与实际功率谱匹配。

为了克服这些缺点,Yule通过用线性回归方程模拟时间序列,奠定了现代谱估计的基础。随后,国内外学者在此基础上进行研究和改进,极大促进了现代谱估计法的发展。

参数模型法是现代谱估计的重要内容,它将信号看成是随机输入序列通过线性系统的输出,由此建立模型来估计信号的功率谱。参数模型估计法主要有自回归(AR)模型、移动平均(MA)模型和自回归-移动平均(ARMA)模型。

AR模型是全极点模型,由线性方程组描述;MA模型是全零点模型,可用高阶的AR模型来近似;ARMA模型是极点和零点共存的模型,由非线性方程描述。本文主要分析AR模型对不同参数的估计方法及ARMA模型的性能,并通过仿真实例研究了不同方法对模型参数估计精度的影响。

1 AR模型

对于AR模型,其数学表示式为:

式中:u(n)、x(n)为实平稳的随机信号,u(n)为白噪声,方差为 σ2。

则其正则方程为:

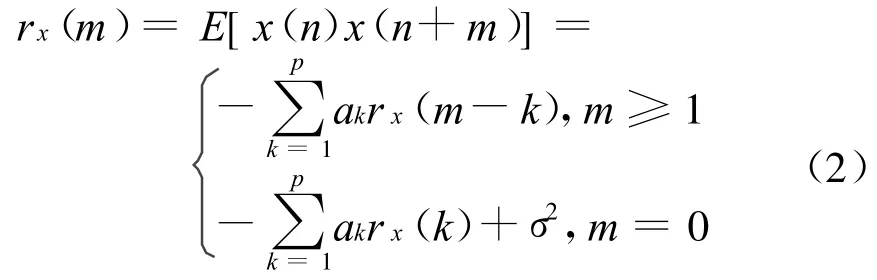
式中:rx(m)为 x(n)的自相关函数;a1,…,ap,σ2为p阶AR模型的待求参数。

若已知自相关函数rx(0),rx(1),…,rx(p),根据正则方程求出模型参数,并估计出信号x(n)的功率谱。当只约束前向预测误差,即为直接法;当对前后向预测误差均做约束时,即为Burg算法。

2 ARMA模型

ARMA模型是AR模型及MA模型的综合。ARMA模型的求解步骤为:根据相关函数得到AR参数a(k),k=1,…,p,并据此用有限冲激响应(FIR)滤波器对输入数据进行滤波,近似得到MA模型,求得MA参数b(k),k=1,…,q,从而得到ARMA模型的功率谱。根据AR模型及MA模型正则方程的推导,则可得 ARMA模型的正则方程为:

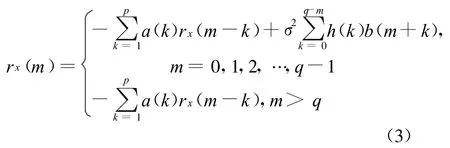
式中:h(k)为a(k)和b(k)的函数。

3 仿真实例

算例中,仿真信号x(n)为白噪声通过三阶FIR系统后输出信号混叠3个不同频率的实正弦信号。白噪声的均值为零,方差为1。各正弦信号的归一化频率为 f1=0.18,f2=0.3,f3=0.31;幅度为A1=1.4,A2=52.6,A3=57.2。

3.1 AR模型自相关法估计信号功率谱

由于模型参数估计中,模型阶数的选择也会对模型参数的求解精度产生影响,因此,在仿真中也充分考虑了这一点,分析比较了不同阶次对参数估计的影响。图1为模型阶数p=5,10,15,20时信号的频谱估计图。

图1 自相关法不同阶数下信号功率谱估计

由图1可知,自相关法对小信噪比信号(f1=0.18)识别能力差,谱估计质量与模型阶次的取值有直接关系,当模型阶数较小时,无法分辨出相邻频率(f2=0.3,f3=0.31)的信号;随着阶次的增大,其对相邻频率的分辨力提高,能识别出相邻频率信号,但可能产生谱分裂现象(如p=25时,在0.18附近)。

3.2 AR模型Burg法估计信号功率谱

同样在仿真中,也比较不同阶次下对Burg法参数估计精度的影响,并将估计结果与自相关法的估计结果进行比较。图2为模型阶数为p=5,10,15,20时信号的频谱估计图。

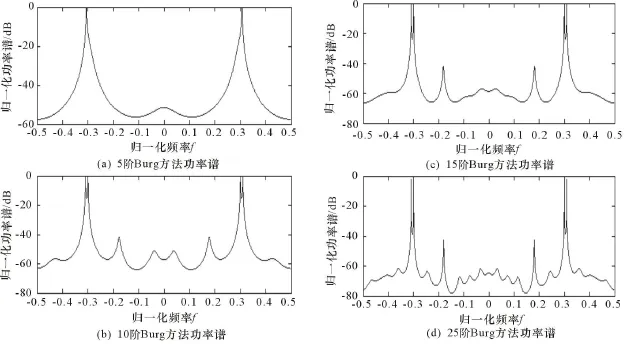
图2 Burg法不同阶数下信号功率谱估计

由图2可知,Burg法对功率谱的估计效果要好于自相关法,这是由于其对前后向预测误差均有约束。因此,Burg法不仅能识别小信噪比信号(f1=0.18),而且可识别相邻峰值的2个信号(f2=0.3,f3=0.31)。随着模型阶次的增加,信号的分辨率增大,但会产生虚假的峰值(如阶数p=25时)。

3.3 ARMA模型估计信号功率谱

仿真条件同上,则不同阶次下ARMA模型估计的功率谱如图3所示。

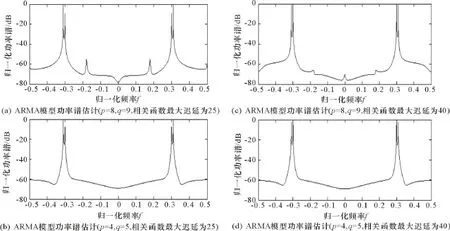
图3 ARMA模型不同阶次下,不同时延对应的功率谱估计

由图3可知:ARMA模型对功率谱的估计效果与模型阶次及信号自相关函数最大延迟的选取有关。当模型阶次选择不恰当时(p=4,q=5),无法识别小信噪比信号。模型阶次确定后,当最大延迟取值为40时,对小信噪比信号(f1=0.18)的识别不明显,且由于MA部分的加入,使得波谷产生,模型对信号谱估计比较容易产生频率漂移现象。