基于匹配模板的二相编码信号识别方法
2010-06-28莫翠琼潘继飞
祝 强,莫翠琼,潘继飞
(1.电子工程学院,合肥 230037;2.安徽省电子制约技术重点实验室,合肥230037)
0 引 言
现代电子对抗信号环境日趋复杂、交错,雷达体制愈加多变,威胁雷达的种类和数量也在不断增加。低截获概率(LPI)技术使雷达信号识别面临新的挑战。目前,国内外的雷达信号识别技术研究思路基本相同,均集中在信号参数提取方法上,具体说,多为利用计算机技术和模式识别技术来实现信号自动识别。但是,当信号较弱、参数提取困难时,无法有效完成雷达信号的检测与识别。数字接收机的研制与投入使用为解决这一问题提供了新的思路。本文提出的匹配模板法基于数字接收机,采用数字信号处理方法进行LPI雷达信号——二相编码信号的截获与识别。
1 匹配模板识别方法的基本思路
数字接收机的一个巨大优势是可以将截获到的雷达信号存储起来,进行事后分析。如果先期在雷达信号主瓣或者信号条件良好的情况下截获到二相编码信号并且成功分析,就可以制定针对该信号的匹配模板,构造匹配滤波器;当信号再次出现时,完成匹配接收与识别。匹配模板识别方法的关键步骤包括匹配模板的创建、匹配算法的实现和匹配输出性能参数的提取与分析这3个方面。
1.1 匹配模板的创建
匹配模板法属于单个脉冲雷达识别范畴。匹配模板的制作可在时域进行,也可在频域进行。时域模板就是直接保存的脉冲数据,长度为一个整脉冲。频域模板是以一个整脉冲数据为数据源,选定模板长度,对数据源进行分段傅立叶变换并且叠加,段长度为模板的长度。两种模板的使用方法大体相同。
理想匹配模板是“干净”的、不受任何污染的,这样的模板比较难以获得。在实际工程应用中,当信号环境良好时,雷达侦察接收机在截获雷达信号后,通过脉内特征分析器准确获取信号参数,数字接收机将这些雷达信号数字化后存储起来,作为匹配模板。当感兴趣的雷达信号再次出现时,与模板库中的雷达信号进行匹配处理,将会获得较大的处理信噪比,实现低信噪比条件下的匹配接收;根据匹配输出结果,判断输入信号是否与模板库中的信号相匹配,一旦满足匹配的条件,即完成识别。
根据匹配滤波器理论,设输入信号为s(t),其频谱为S(ω),则其对应的匹配滤波器的脉冲响应为h(t)=kS*(t0-t),t0为信号输出最大时刻。匹配滤波器在频率域的特性为 H(ω)=kS*(ω)◦exp(-jω t0)。模板创建过程就是匹配滤波器频率响应获取的过程。
1.2 匹配算法的实现
匹配滤波器的输出为y(t)=s(t)⊗h(t),⊗为卷积符号。根据傅里叶变换理论,时域的卷积等效于频域的乘积,可得Y(ω)=S(ω)H(ω),这是频域处理的理论基础。图1为频域处理的原理框图。
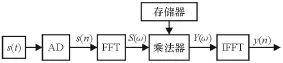
图1 频域处理原理框图
频域处理首先将截获的雷达信号进行采样,数字化后再进行快速傅里叶变换(FFT),与事先存储在匹配模板库中的数字谱相乘,得到的结果使用快速傅里叶逆变换(IFFT)还原为时间离散信号,计算表达式为:
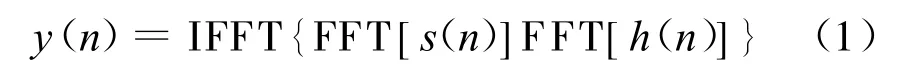
假设输入信号s(n)的点数为 N1,模板h(n)的点数为N2,那么FFT的点数可以确定为:
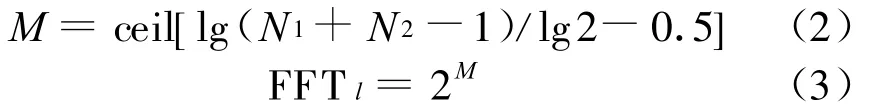
式中:ceil表示向上取整。
如果滤波器中存储有输入信号的数字谱,那么它相对于输入信号便构成了匹配滤波器。对于此时特定的匹配模板,匹配输出结果是一定的,这点可以从下面的计算机仿真得到验证,据此便能判别输入的雷达信号。
1.3 匹配输出性能参数的提取与分析
相位编码信号的复数表达式为:
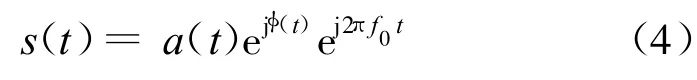
信号的复包络函数为:
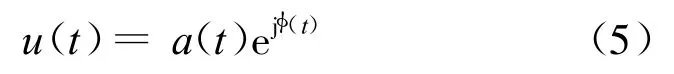
式中:φ(t)为相位调制函数。
对二相编码信号来说,φ(t)只有0或2π两个可能取值。如果二相编码信号的包络为矩形,则二相编码信号的复包络为:
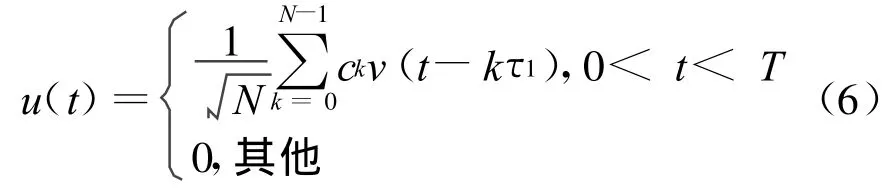
式中:v(t)为子脉冲函数;τ1为子脉冲宽度;N为码长;T=Nτ1为编码信号持续期。
用傅里叶变换不难得到二相编码信号的频谱:
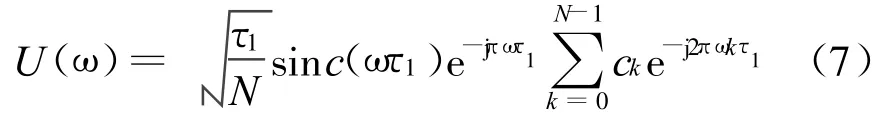
用频域处理方法,以二相编码信号为例研究匹配输出性能。模板信号各参数为:f0=160MHz,N=13,T=13 μ s,τ1=T/N=1 μ s。当输入信号为二相编码信号且各参数与模板信号参数相同时,由式(1)可得匹配处理的时域波形,见图2。
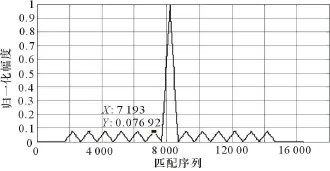
图2 理想匹配处理结果
通过对理想匹配输出性能参数的提取与分析,可以制定针对二相编码信号的匹配识别准则:主副瓣形状都为三角形,且副瓣三角形高度相等,均为码长的倒数,即1/N;主副瓣个数之和等于码长的倍数。只要输出的结果同时满足以上2点,就能说明该信号为二相编码信号。
2 计算机仿真
除理想匹配处理外,输入信号与模板信号还存在以下2种关系:输入信号与模板信号类型不同;输入信号与模板信号类型相同,但不是同一雷达信号。
2.1 输入信号与模板信号不是同一类型信号时匹配处理结果
当模板为二相编码雷达信号时,理想的匹配输出结果是输入信号和模板信号相同的情况。当输入信号与模板信号不是同一类型信号时,最容易判别输入信号不是期望信号。例如,模板信号为二相编码信号,当输入信号分别为简单脉冲与线性调频信号时,匹配输出结果如图3所示,对照匹配识别准则,与理想结果相差甚远,可以很快判定信号不是期望信号。
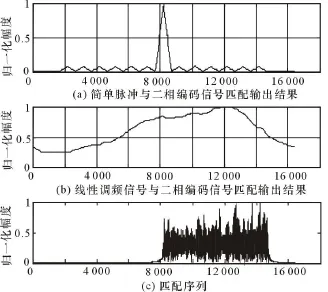
图3 信号类型不同时匹配输出结果比较
2.2 信号类型相同,参数不同时匹配处理结果
当其他参数均相同,输入信号的载频 f0依次为160MHz、159MHz、158MHz、 157MHz、161 MHz、162 MHz时匹配输出结果如图4所示。
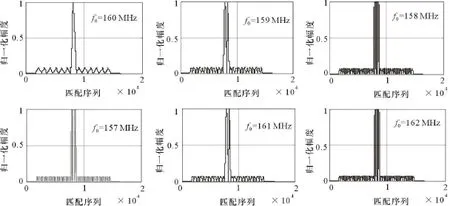
图4 载频不同时匹配输出结果比较
表1计算出了匹配输出性能参数。从计算结果看,主副瓣幅度保持不变,但输出的主副瓣个数随输入信号载频与模板信号载频之差的变化而变化。假设载频之差为n,则输出主副瓣个数之和为码长的2n倍,根据匹配识别准则,可以判定输入信号为期望信号。当其他参数均相同,输入信号的码长 N依次为13、11、7、5时匹配输出结果如图5所示;当其他参数均相同 ,子码宽度 τ1 依次为 1 μ s、2 μ s 、3 μ s、4 μ s时匹配输出结果如图6所示。
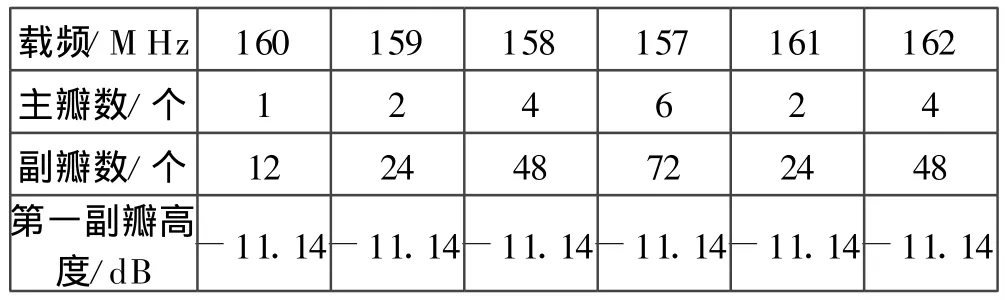
表1 匹配输出性能参数分析
在这2种情况下,匹配输出的结果与理想结果相差甚大,无法计算性能参数,此时可以判定输入信号不是期望信号。也由此可见,要想得到二相编码信号的理想匹配输出结果,对输入信号参数的要求比较苛刻。
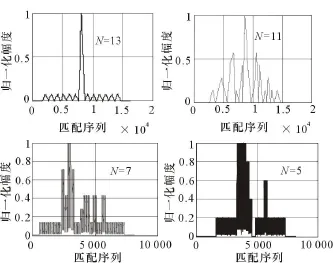
图5 码长不同时匹配输出结果比较
2.3 噪声对匹配识别结果的影响
当输入信号与模板信号匹配,但是受到了噪声的污染,此时将会对匹配输出性能参数的提取带来一定影响。图 7绘制出了信噪比分别为10 dB,0 dB 、-5 dB、-6 dB、-8 dB 、-10 dB、-12 dB 的匹配识别结果,表2计算出了匹配输出性能参数。从计算结果看,随着噪声的增大,峰值位置出现少许的偏移,副瓣高度呈现增高的趋势,但根据匹配识别准则,仍然可以识别出该信号。
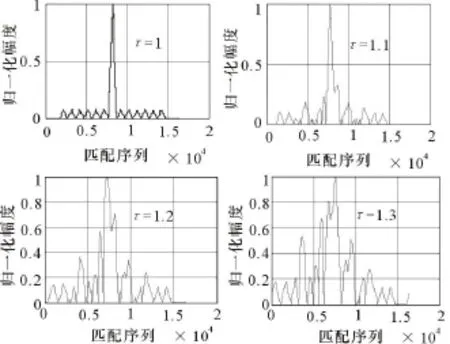
图6 子码宽度不同时匹配输出结果比较
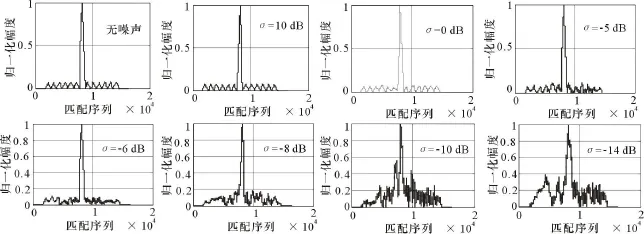
图7 噪声对匹配识别结果的影响

表2 匹配输出性能参数分析
3 结束语
本文介绍的匹配模板法是基于先期获取敌方二相编码信号数据并且制定出匹配模板的前提下进行的,由于匹配模板的唯一性,决定了该方法只对期望信号有效。文中通过对输入信号与模板型号可能存在的几种情况进行仿真实验,验证了匹配准则的有效性和该方法的可行性。当输入信号为期望信号时,识别信噪比可以达到-6 dB。在实际应用中,采用二相编码信号制作匹配模板,当期望信号再次出现时即可以成功截获并识别。
[1]Phillp pace.Detecting and Classifying LPI Radar[M].Norwood:Artech House,2003.
[2]孙垦.雷达数字化接收机[J].舰船电子对抗,2003,26(4):32-33.
[3]姜秋喜,潘继飞,毕大平.匹配模板法在雷达信号识别中的应用[M].电视技术,2005(5):31-35.
