基于摩尔型CA置乱的DCT域数字水印技术*

韦春荣，刘俊景

（1.广西师范大学 电子工程学院，广西 桂林 541004；2.桂林电子科技大学 教学实践部，广西 桂林 541004）

1 引言

作为数字认证和版权保护的重要手段，数字水印技术近年来已成为信息安全和多媒体信号处理领域研究的热点。数字水印技术的性能指标主要有安全性、稳健性和不可见性等。数字水印算法主要可分为空域和变换域算法两大类。变换域算法因其对几何攻击处理和常见的图像处理具有较强的稳健性能而具有更好的应用前景。文献[1]提出一种基于二维元包自动机的图像置乱和水印技术，该算法在空域数据进行水印信息嵌入，算法简单，速度比较快，但嵌入的水印很容易被普通的图像处理所破坏，算法稳健性比较差；文献[2]提出一种基于分块的DCT域数字图像水印算法，将伪随机序列嵌入一组被选的DCT系数中，虽然水印的稳健性较好，但不可见性欠佳。笔者在前人研究的基础上，提出了一种基于摩尔型元胞自动机置乱加密的DCT域数字图像水印算法，实验结果表明该算法在不可见性和稳健性方面取得良好的平衡。

2 基于摩尔型元胞自动机的图像置乱

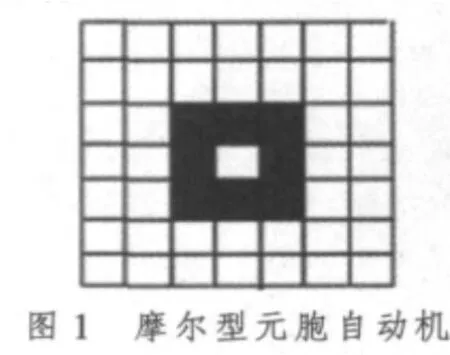
元胞自动机[3]（Cellular Automata，CA）是一个时间、空间和状态变量取值均离散的动力系统。它是由大量简单、具有局域相互作用的元胞构成。每个元胞处于状态空间中的某种状态，各个元胞在t+1时刻的状态值根据一个预定义的局部规划，按照其t时刻的邻域函数规则进行同步更新。近年来，CA成为模拟复杂物理系统和同步并行过程等学科领域的研究热点[4-5]。二维摩尔型CA为图1中所示的3×3邻域网格模型。文献[1]研究表明部分规则号的摩尔型CA的动力学行为具有混沌性质，能较好地被应用到图像加密和水印技术中。为加强水印信息的安全性，消除各像素的空间相关性，在水印嵌入之前，首先取具有混沌性质的规则号C=244，局部规则为外全加规则，对应的映射函数为 f（1，2）=1，f（0，3）=1，f（1，3）=1，其他状态值为0的摩尔型CA对原始水印图像进行置乱。待置乱的原始水印图像为图2所示的 200×200×8 bit二值图像。

置乱具体步骤描述如下：

1）随机产生一个 200×200的 0，1分布矩阵 A0（即为初始随机种子矩阵）。

2）将A0的状态值为1的点对应到要置乱图像W的像素点上去，并且按行顺序取出放到新建的图像像素矩阵W′中去。

3）用规则号C=244的映射函数f对A0进行连续迭代 k 次得出一序列｛A1，A2，A3，…，Ak｝。

4）取与A1状态值为1，且A0相同位置状态值不为1的点对应图像W上的像素灰度值并按顺序取出放到W′后面。

5）继续迭代到第k步，取出Ak状态值为1而在Ak-1，Ak-2，…，A1，A0的相同位置状态值全不为1的点所对应的图像W上的像素灰度值，依次放到W′中。最后，将图像W中剩下的点也依次放到W′中。这样所得到的W′就是进行置乱加密后的图像。图3为迭代次数k=3时所得到的置乱结果图，可见，置乱处理后降低了水印图像像素的相关性。解密用此算法的逆过程，需要用的密钥是初始随机种子矩阵A0、迭代次数k和规则号C，丰富的密钥提高了水印信号的安全性。

3 载体图像的DCT及水印嵌入域的确定

离散余弦变换（Discrete Cosine Transform，DCT）是一种基于实数的正交变换，常用于图像编码和压缩，是图像编码的国际标准（JPEG）的主要环节。对于一个N×N矩阵f，二维离散余弦正变换定义如下

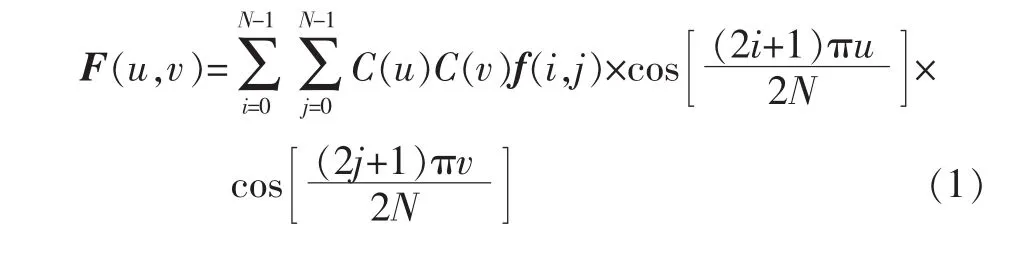
其中，u和 v的取值为 0～N－1。

二维离散余弦反变换定义为

式中，i和 j的取值为 0～N-1，且

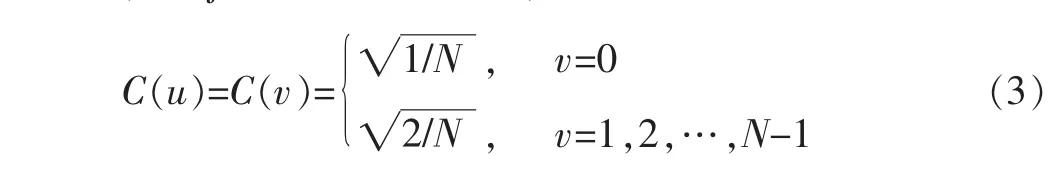
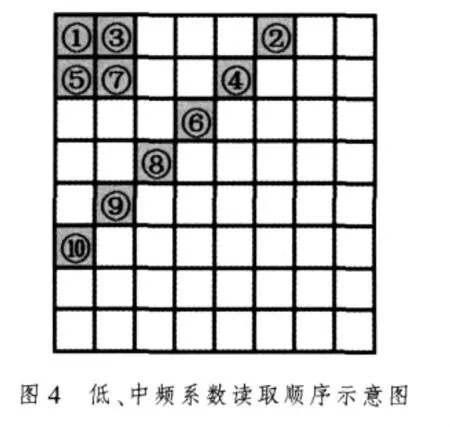
图像在DCT变换后，主要能量集中在少数低频系数中（即DCT矩阵的左上角），纹理和边缘信息集中在中频系数中。如果在低频中嵌入水印，即使图像发生一些失真，但只要主要部分保留（视觉质量不降低）不丢失，那么嵌入信息也不会丢失，从而保证水印算法的稳健性能。但是人眼对低频系数最为敏感，低频系数的轻微改变会引起察觉，因此考虑到水印的不可见性，不应对低频系数作较大改变。另一方面，人眼对高频系数不敏感，将水印信息嵌入高频中可以提高水印嵌入的不可见性，但是高频系数接近零值，在滤波和有损压缩时容易造成数据丢失，稳健性不好。基于对各频段特点的分析，笔者根据嵌入水印信息量的大小合理选择在图像DCT域的部分低频系数和中频系数中嵌入水印信息。为了与国际JPEG压缩标准一致，先将载体图像分成8×8的互不重叠小块，并分别对每一块进行DCT变换，再按图4序号所示顺序依次读取低频、中频系数构成与水印图像同样大小的系数矩阵，并在该系数矩阵的奇异值分解 （SVD）域中嵌入水印信息。此处应用SVD的主要原因有：1）图像奇异值的稳定性好，当图像受到轻微扰动时，它的奇异值不会发生剧烈的改变；2）奇异值所表现的是图像的内蕴特性而非视觉特性[6-7]。因此在图像的奇异值中嵌入水印对几何攻击将具有很好的稳健性。

4 数字图像水印的嵌入和提取

设原始载体图像为I，水印图像为W。本文的水印嵌入算法结构框图如图5所示。

水印的提取算法是水印嵌入算法的逆过程，水印的提取过程中需要水印嵌入过程中的矩阵U1，V1，S和水印信息解密密钥的参与，限于篇幅，此处不再赘述。

5 算法仿真及分析

在Matlab R2009b环境下笔者对所提水印算法进行了大量的仿真实验。实验中选用的原始载体图像为512×512×8 bit标准灰度Lena图像 （见图6），数字水印采用200×200×8 bit的二值图像（见图7），嵌入强度因子取a=0.2。图8、图9表示在无任何攻击时本文算法所得的含水印的Lena图像及提取的水印。可见，在无任何攻击的情况下，本文算法能有效地完成水印信息的嵌入和提取。

为了对该算法进行客观的评价，本文对含水印Lena图像进行常见攻击后再从受攻击图像中提取水印信息，除通过视觉判定外，还采用峰值信噪比（Peak Signal Noise Ratio，PSNR）作为嵌入水印对原始载体图像引起失真程度的度量指标，采用归一化相关系数（Normalized Correlation，NC）作为提取水印与原始水印相似度的评价指标。PSNR值越大，表明对原始载体图像的破坏越小，即嵌入水印的不可见性越好；NC值越大，表明两者的相似度越大，即水印提取效果越好。峰值信噪比定义为

归一化相关系数定义式为

式中：W（i，j）为原始水印像素值；W′（i，j）为提取的水印像素值；M和N分别为水印的宽度和高度。

含水印图像经历常见攻击如JPEG压缩、滤波、噪声和几何攻击后的PSNR值与提取水印NC值如表1～3所示。

表1 含水印图像经历JPEG压缩后PSNR值和NC值

表2 含水印图像经历噪声、滤波后PSNR值和NC值

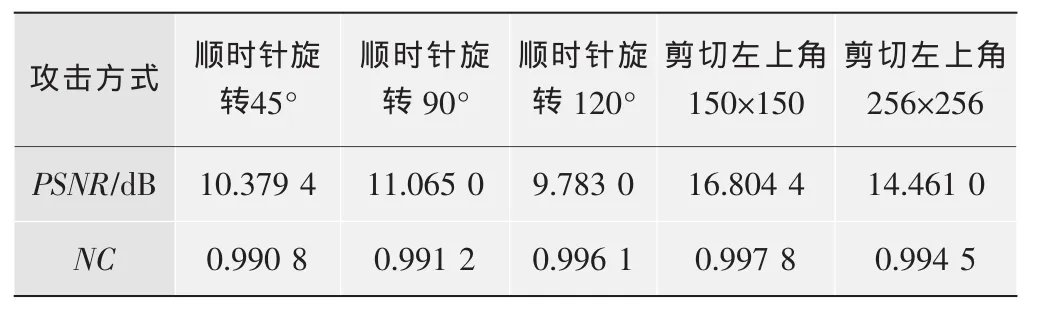
表3 含水印图像经历旋转、剪切后PSNR值和NC值

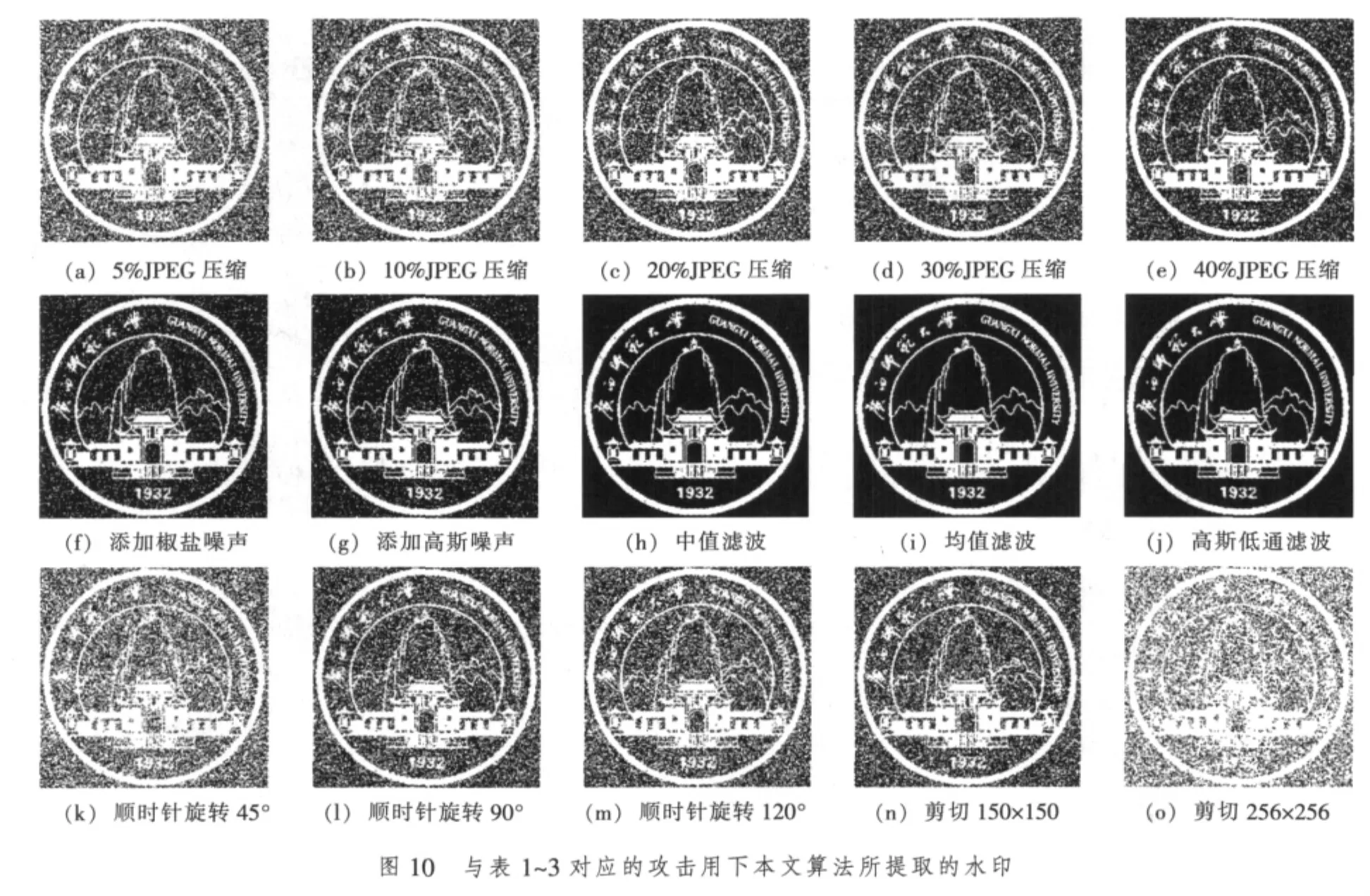
表1～3实验数据及图10的水印提取结果表明：1）本文算法具有良好的不可见性；2）该算法具有很强的抗低通滤波、噪声干扰的能力，同时对JPEG压缩、旋转和剪切等攻击表现出较强的稳健性；3）本文算法所提取的水印在对角线上没有失真现象。

6 小结

提出了一种基于摩尔型CA置乱的DCT域数字图像水印算法，利用摩尔型CA的混沌特性对原始水印进行置乱加密，不仅降低了水印图像像素的相关性，提高水印的安全性，而且消除了基于SVD数字水印算法提取水印在对角线上的失真问题。另外，算法能综合图像DCT变换低频系数和中频系数的特点，自行根据嵌入水印信息量的大小合理确定在图像DCT域的部分低频系数和中频系数，并按预定顺序选取相应频率系数构造奇异矩阵，最后在该系数矩阵的SVD域中嵌入水印。仿真实验及攻击测试结果表明，该算法在水印的不可见性和稳健性之间取得了较好的平衡，在版权保护领域具有一定的应用价值。

[1]李辉亮，叶瑞松.基于二维元胞自动机的图像置乱和水印技术[J].中国图象图形学报，2008，13（11）：2076-2080.

[2]BARNI M，BARTOLINI F，CAPPELLINI V，et al.A DCT-domain system for robust image watermarking[J].Signal Processing，1998，66（3）：357-372.

[3]周成虎，孙战利，谢一春.地理元胞自动机研究[M].北京：科学出版社，2001.

[4]苏磊，周金旺，谭惠丽，等.考虑驾驶员特性的混合交通流演化网络特性研究[J].广西师范大学学报∶自然科学版，2009，27（1）：5-8.

[5]龙贵忠，孔令江，刘慕仁，等.NaSch模型的细化研究[J].广西师范大学学报∶自然科学版，2008，26（3）：5-8.

[6]刘瑞祯，谭铁牛.基于奇异值分解的数字图像水印方法[J].电子学报，2001，29（2）：168-171.

[7]INGEMAR J， KILIAN J， LEIGHTON T， et al.Secure spread spectrum watermarking for multimedia[J].IEEE Trans.Image Processing，1997，6（12）：1673-1687.