金融效率、经济增长与收入不平等——一个内生增长模型的解释

师文明，余晓辉

（1.中南财经政法大学 经济学院，湖北 武汉 430073；2.深圳大学 高级研究中心，广东 深圳 518060）

一、引言

20世纪90年代以前的金融发展理论很少正式研究收入分配问题，只是一些金融发展模型隐含了金融发展对收入分配作用的结论，缺乏系统研究的文献。比如，在M-S模型中，McKinnon （1973）和Shaw（1973）认为，发展中国家的金融抑制、信贷配给，放慢了经济增长，加重了社会收入分配不均。麦金农研究了金融抑制与二元经济结构的关系后得出结论：在金融抑制条件下，在取得信贷的不同等待遇会导致二元经济结构；同时，在取得信贷方面的不同待遇也会导致收入不平等。Galbis（1977）提出的两部门金融发展模型，证明了金融抑制造成了收入分配的不平等。

20世纪90年代以后，金融发展与收入分配的理论研究受到学术界越来越多的关注，国外学者陆续提出了三种不同的理论假说。一是有益论；Galor和Zeira（1993）构造了一个世代交叠和代际利他的两部门均衡模型，并假设个体只有进行了不可分割的人力资本投资，才能就业于高收入的现代部门，否则只能在传统部门从事低收入的工作。金融自由化、金融市场的竞争和向更多地民众开放，使穷人也能通过融资进行人力资本投资，进入高收入的现代部门。二是有害论；Maurer和Haber（2003）认为，金融发展与深化，并没有使金融服务向穷人和新企业延伸。金融服务，尤其是信贷服务依然只是针对富人和具有某种政治联系的企业，并使它们的相对收入进一步上升。他们指出，在社会精英统治的国家，金融深化不是增强而是减弱了金融市场的竞争，增进了高收入者的福利，而牺牲了低收入者、中产阶级的利益，这实际上增加收入不平等程度。三是倒U字型关系论；在Greenwood和Jovanovic（1990）看来，金融发展与收入分配之间并不是简单的正向或反向线性关系，而是一种倒U字型关系。他们证明了在经济发展初期，收入分配不平等状况会加剧；而随着经济增长和金融中介规模的扩大，越来越多的人可以加入金融中介，收入分配差距最终将缩小，直至收敛到平等水平，即金融发展和收入分配的关系服从“倒U”型的轨迹。因此，GJ模型是库兹涅茨假说的一种扩展形式。Townsend和Ueda（2006）在GJ模型的基础上进行简化和改进，以更统一的动态模型讨论金融深化对收入分配的影响及其动态演化路径，论证金融发展与收入差距的关系也遵循库兹涅茨曲线。

在理论研究方面，大多数模型都是用金融发展规模来表示金融发展水平。比如，在Greenwood和Jovanovic（1990）构建的GJ模型中，在经济增长后期，随着金融中介规模的扩大，才会有更多的人享受金融服务，从而逐步降低收入分配差距。这样的结论对发达国家可能是适用的，而对于大多数发展中国家却不一定适用。因为很多发展中国家虽然具有庞大的金融中介体系以及金融规模，但却并不意味着这些国家具有很高的金融发展水平。发展中国家庞大的金融中介规模很可能是金融抑制以及制度和信息基础的不完善，甚至是金融效率低下、投资渠道不畅通造成的（陈志刚，2006）。Galor和Zeira（1993）的模型则使用借贷利率作为金融发展水平的度量标准，认为借贷利率越低，金融发展水平就越高，反之则越低。但是这实际上隐含了一个假设，那就是利率必须是市场化的。而很多发展中国家，比如中国，并没有实行利率的自由化，所以其模型的适用性存在局限。为了解决金融发展规模不能准确反映一国金融发展水平的问题，很多学者在实证研究中采用了金融效率指标（姚耀军，2005；陈志刚、师文明，2008等），但学者们并没有从理论上构建模型分析金融效率对收入不平等的影响，其实证结论缺乏理论支撑。因此，本文尝试在Garcia-Penalosa和Turnovsky（2006）劳动内生供给的内生增长模型基础上，加入金融部门，分析金融效率提高对经济增长和收入不平等的影响。

二、基本模型

（一）技术和要素支付

鉴于关于金融发展与收入不平等的关联机制分析，我们把经济分为实物部门和金融部门。实物部门的产出分为消费C和储蓄S，其生产过程使用了原有的资本存量K和劳动力L。企业用j表示。我们假定代表性企业的生产函数为Cobb-Douglas生产函数①：

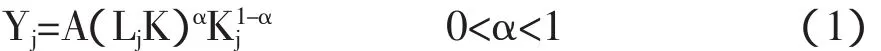
其中Kj表示个体企业的资本存量，Lj表示个体企业使用的劳动力，K是经济中的平均资本存量；所以LjK度量的是企业雇佣的有效劳动力。生产函数对私人要素——劳动和私人资本存量表现出规模回报不变。

所有的企业面临相同的生产条件。因此它们将选择相同水平的劳动力和资本存量。也就是说，Kj=K和Lj=L对于所有的j，其中L是经济中平均劳动力使用水平。我们进一步假定，总体劳动力市场出清使得L=1-l，其中l是总体休闲时间。经济中的资本存量产生外部性使得均衡时总（平均）生产函数对于总资本存量是线性的，这和Romer（1986）一样。

其中Ω（L）=ALα，并且∂Ω/∂L＞0。

我们假定工资率ω和资本回报率r是由它们相应的边际实物产出决定的。给定所有企业都是相同的，对生产函数进行求导，我们得到作为休闲时间函数的均衡要素价格：

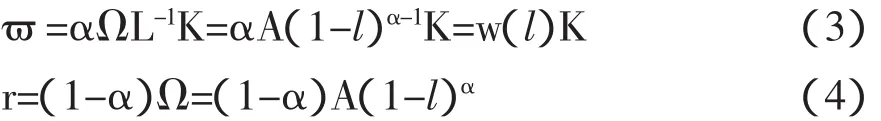
上面两式意味着，资本的均衡回报与资本存量无关，而工资率与平均资本存量成正比，并因此随着经济增长而增长②。另外，我们还有∂r/∂l＜0和∂w/∂l＞0，这说明了更高的劳动使用量（更少的休闲时间）会提高资本生产率但是会降低劳动生产率。

（二）金融部门

金融部门的作用主要体现在如何有效地将储蓄转化为投资，假定其效率主要表现为储蓄向投资的转化率θ，从而有下面的储蓄——投资转化方程：

（三）消费者

经济中个人的寿命是无期限的，消费者i除了他们的原始资本禀赋Ki0之外在各个方面都是完全相同的。因为经济是增长的，我们需要关注个人i在总资本存量中所占的份额ki，定义ki=Ki/K。相对资本ki有一个分布函数G（ki），其均值为∑iki=1，方差为σ2k。

所有的个体都拥有一单位的时间，可以被用来休闲li或者用来工作Li=1-li。代表性消费者最大化其一生的期望效用，效用函数中包含消费和一定数量的休闲：

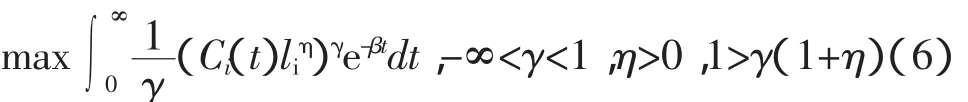
其中e≡1/（1+γ）等于跨期替代弹性。③大量的经验证据表明，e相对比较小，甚至可能小于1，因此我们假定γ＜0。参数η代表了效用中的休闲弹性。该最大化问题的个体资本积累约束为：

由于均衡的工资率与总资本存量相关，所以我们可以从（7）式中观察到，个人的资本积累率依赖于总资本存量，而对于个人而言总资本存量相当于是给定的。为了简单起见，我们的模型中不考虑政府。

三、模型的均衡

（一）消费者最优化

消费者最优化问题就是在积累方程（7）的约束下，选择消费率、休闲率和资本积累率来最大化效用函数（6）。相应的一阶条件为：

其中，λi是个体i资本的影子价格，并且横截性条件为：

（二）宏观经济均衡的推导

由最优化条件、个人的积累方程和整体经济的相关条件，我们可以推出宏观经济的均衡状态，并且证明经济总会在它的平衡增长路径上。我们用（8）式除以（9）式可以得到：

我们可以把个人的积累函数（7）式写成下面的形式：

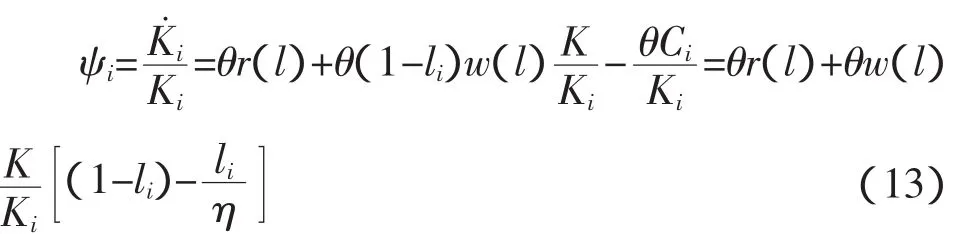
将（8）式对时间t求导，并结合（10）式和（5）式我们可以得到：

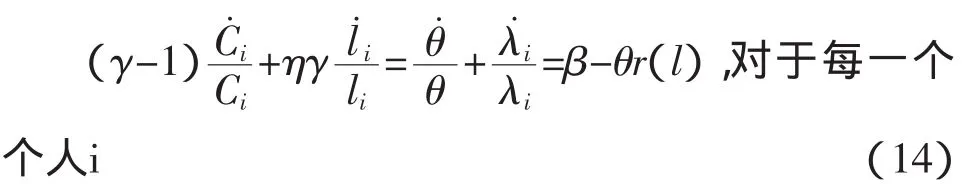
（9）式的重点在于，不考虑个人资本禀赋的情况下，每个人都选择相同的资本影子价格增长率。将（12）式对时间t求导我们可以得到：

现在对个人i和k考虑方程（14）和（15）。我们可以得到：

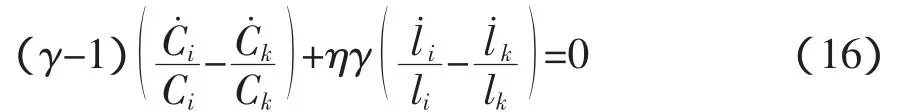
由上面两式，我们可以得到：

也就是说，所有的个人都将选择相同的消费和休闲增长率。反过来，这也意味着平均消费C和平均休闲也以他们各自相同的增长率而增长。

现在让我们回到总体经济。将（12）式加总起来并且注意∑iki=1和∑ili=l，总体经济系统的消费－资本比率为：

我们加总（13）式可以得到总的积累方程④：

接下来的推导是为了证明，在均衡状态下l（t），li（t），ki（t）≡Ki（t）/K（t）随着时间是不变的，经济实际上总是在它的平衡增长路径上⑤。为了证明这个结论，我们将（20）、（15）和（18）式带入（14）式，并将它写成的微分方程形式：

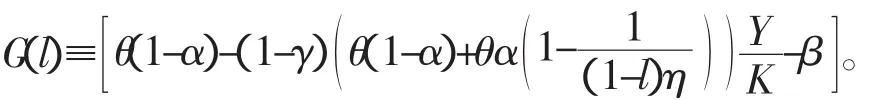
因为时间是有限的，所以在稳定均衡状态有l˙=0，并且相应的l的稳定水平由G（l）=0决定。那么l关于的线性化动态方程为：

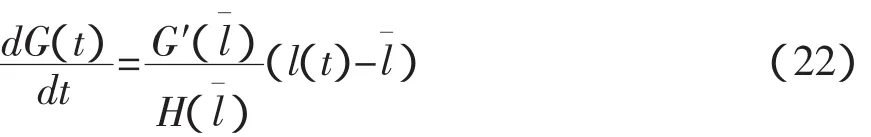
在γ＜0的条件下，横截性条件可以保证G'（l¯）＞0，那么在这个条件下，（22）式就是一个不稳定的微分方程。因此，最终达到均衡状态的唯一解就是使得l（t）在任何时间点上都是不变的。由（18）式可知，li（t）在任何时候也是不变的。

接下来就是将（13）式和（20）式结合起来得到下面相对资本存量ki（t）≡Ki（t）/K（t）的微分方程：

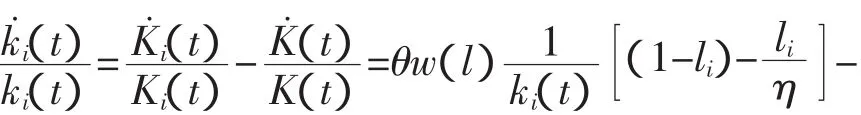
进一步我们可以得到：

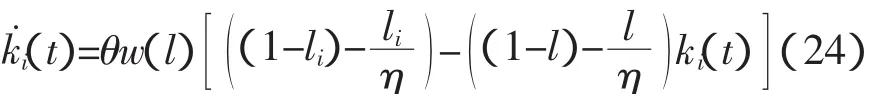
（24）式描述了从初始禀赋k0开始，相对财富（资本）的变化情况。由于li和l都是固定不变的，如果u和θ在某一个固定的水平上，那么这就是一个简单的线性方程。该方程的性质就依赖于系数ki（t），而系数ki（t）又由横截性条件决定。如果（11）式的横截性条件对所有的个人都是固定不变的，那么我们可以得到总的横截性条件：

由于l是固定不变的，那么由（14）式和（20）式可知λ和K都以固定的速率增长。因此，可以直接证明，（25）式要成立当且仅当

也就是说，金融部门中资本回报的均衡速率必须大于经济的均衡增长率。根据（20）式中的两个方程，我们可以把横截性条件进一步写成下面两个等价的形式⑥：

第一个方程表明个人的资本收入被消费了，而后一个方程表示满足这种情况的休闲约束。

现在回到（24）式，由（28）式我们可以知道，如果系数ki是正的，那么这就意味着，满足长期稳定性和横截性条件的唯一解就是（24）式的右边为零。也就是说对于所有的时间，K˙i=0。因为ki反映的是资本存量随着时间变化的情况，所以个人可以通过“相对劳动供给”函数⑦选择他们相应的休闲li来实现。“相对劳动供给”函数形式为：

那么，由横截性条件（28）式可以得到相对财富和休闲之间存在正向的关系，因而个人的相对财富状况ki随时间是不变的。所有个体的资本存量都以相同的速率增长，这意味着在任何时刻，个体i的份额ki都等于他的初始份额ki，0。更进一步，由（14）、（15）和（18）式我们可以推出个人消费和总消费也以相同的速率增长：

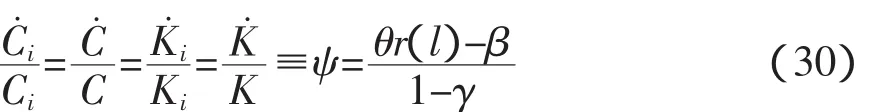
（29）式给出了个人的休闲选择，而（30）式给出了个人的消费增长率。（29）式代表了“相对劳动供给”函数，并且是个人的初始相对资本禀赋影响收入分配的关键因素。越富有的个人具有越低的财富边际效用。因此，他们会选择提供更少的劳动而“购买”更多的闲暇。他们需要补偿更多的资本禀赋，而这会支持更高的增长率。然而通过提供更少的劳动，又会对增长率起到一个抵消的作用。因此，增长率不依赖于资本的分配。

（30）式表明，在均衡状态下，消费和资本的增长率是相等的，并且对所有个人都相同。因此，宏观经济均衡，包括增长率和总体劳动供给，并不依赖于财富分配。更进一步，所有个体的资本存量都以相同的速率增长，这就意味着，个体i的资本份额ki仍等于他的初始份额ki，0。也就是说，个体的相对财富位置随着时间是不变化的。

劳动供给弹性在决定收入分配中扮演的角色类似于它在其它相似的增长模型中所扮演的角色。比如，政府消费支出在拉姆斯模型中会有资本积累的效应，并且当且仅当劳动供给是弹性的时候在拉姆斯模型中具有增长效应。在这两个例子中，下面的这些反应都是由财富效应和它对劳动供给的影响所促使的。

（三）宏观经济均衡

上面的分析表明，经济总是在它的平衡增长路径上，经济中关键的均衡关系总结如下：

（1）均衡增长率

（2）总消费－资本比

（3）产品市场均衡

由r（l）、w（l）和Ω（l）的定义，给定ki，这些方程联合起来就可以确定总的消费－资本比C/K，总的闲暇时间l以及平均增长率ψ。给定1，（29）式确定了个人的休闲时间li，而个人的消费-资本比率可以由（9）式除以（8）式得到，并且表示为：

由（31）、（32）和（33）式，宏观经济均衡可由下面一对方程描述，它们共同决定了均衡增长率ψ和平均休闲时间l：

第一个方程描述了ψ和l之间的关系，这确定了资本回报风险调整比率和消费回报风险调整比率之间的等价关系。第二方程描述了均衡增长率和休闲之间的关系，这确定了产品市场均衡得到了满足。接下来我们将关注它们的解，这个解不仅在满足横截性条件下是稳定的，而且也产生正的均衡增长。由（36）式和（28）式可知，l的均衡解必然在下面这个区间里：

方程RR和PP在图1中被描述出来。⑧首先，方程PP对于l总是递减的，这反映了更多的休闲时间会降低产出，从而提高消费－产出比率，并且对资本增长率会有一个反向影响。另外，RR曲线对于l也是递减的。直观的看，休闲时间所占的比重越大会降低资本生产率，需要降低消费回报。如果消费的边际效用增长上升，也就是说，如果平衡增长率下降，就会产生这个结果。在弱条件下，这两条曲线都是凹的并且存在一个唯一均衡点Q的充分条件是：

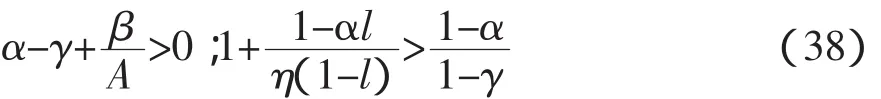
与稳定性条件G′（l）＞0一起，如果γ≤0那么这两个条件都可能满足。因此，它们在更弱的条件下也能满足。

图1 均衡增长、就业和收入分配

（四）收入不平等

现在我们考虑拥有资本存量Ki的个人的相对收入。他的总收入为Yi=rKi+wKi（1-l），而经济的平均收入为Y=rK+wK（1-l）。用方程（29）来替换个人的劳动供给，我们可以将个人i的相对收入写成yi≡Yi/Y，即

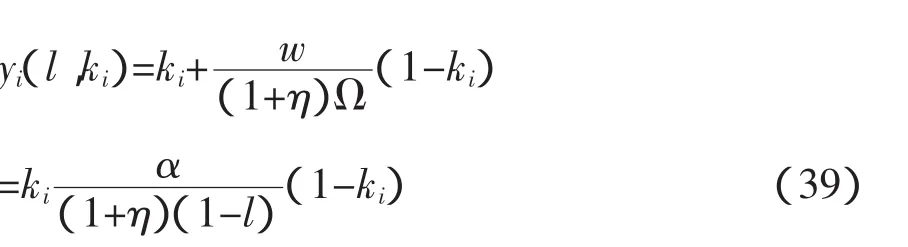
我们可以将上式简化为：

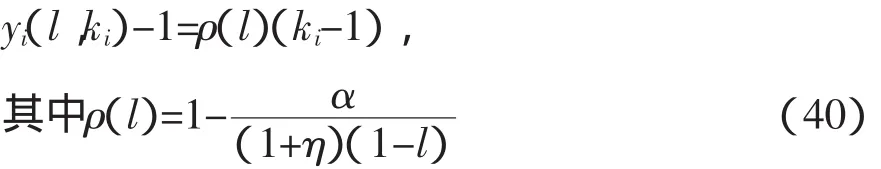
方程（40）强调了收入分配依赖于两个因素，资本的初始分配和时间在劳动与休闲之间的均衡分配。初始财富增加对个体i相对收入的净影响由ρ（l）给出。只要均衡是正增长，那么可以直接证明⑨：

因此，相对收入对于ki是严格递增的，这就表明，虽然更富有的个人选择了更低的劳动供给，但是这种影响并不足以抵消他们更高的资本收入。结果，个体之间收入的标准差σy小于他们资本的标准差σk，其中σy可以用来很方便的度量收入不平等。为了看得更直观一点，相对劳动供给函数即方程（29）意味着，劳动供给的标准差σL=σl可以表示为：

由（28）式可知，（42）式括号中的那一项在0-1之间，这就表明劳动供给分布的不平等程度低于资本禀赋分布的不平等程度，而这又会进一步降低个体之间的收入差异。

沿用Garcia-Penalosa和Turnovsky（2006）的方法，我们也用σy来度量收入不平等。那么，位于图1下面的DD曲线就描述了相对收入的标准差σy和资本禀赋的标准差σk之间的关系⑩。

给定资本的标准差σk，收入的标准差是总体休闲时间的递减和凹方程。这是因为，随着休闲增加（并且劳动供给减少），工资率上升并且资本回报下降，这就把收入差异的范围限制在拥有大量资本禀赋的财富和低于最优禀赋分配的财富之间。

因此，当金融效率θ不变时，由图1上部来决定劳动（休闲）的最优分配，即由点Q表示。那么，（43）式就可以决定个体之间相应的收入标准差σy，由点M表示。接下来，我们将分析金融效率θ发生变化时，如何引起经济增长和收入不平等的变化。

四、金融效率和收入不平等之间的关系

我们假定金融效率θ提高，即金融部门将储蓄转化为投资的能力逐渐增强。从图2我们可以看到，θ的提高导致了PP曲线和RR曲线向上移动，其中PP曲线总是经过横轴上的点T。在θ提高的初始阶段，经济的均衡点从Q和M移动到Q′和M′。RR曲线的向上移动会导致更高的经济增长率和更少的休闲时间。但是，PP曲线（对于ψ＞0）的向上移动会抵消这种效应，它会增加1并降低经济增长率ψ。然而在均衡状态下前者的影响更大，因此新的均衡点Q′具有更高的经济增长率和更少的休闲时间。

更高的经济增长率和更少的休闲时间（劳动时间更长）两者之间并不矛盾。直观上看，经济增长率越高，人们收入的水平更高，休闲时间似乎应该更多才对。但是这只是针对个人而言，经济增长促使个人的收入水平越高，个人的休闲时间应该是更多。而这里的休闲时间指的是全社会的休闲时间，而非个人的休闲时间（同注释⑩）。经济增长率越高，会造成社会需要的劳动力越多，对于某些人而言，休闲时间可能是增加的，但是对于整个社会而言，休闲时间可能就是减少的。

根据DD曲线，新的均衡点Q′对应的收入标准差σy更大（由图2中点M′表示）。也就是说，金融效率θ提高会导致更高的收入不平等。因此，我们可以得出以下命题：

命题：金融效率的提高会导致更高的经济增长率，但同时也会增加收入不平等程度。

证明：由（35）和（36）式我们可知，点Q由下式决定：

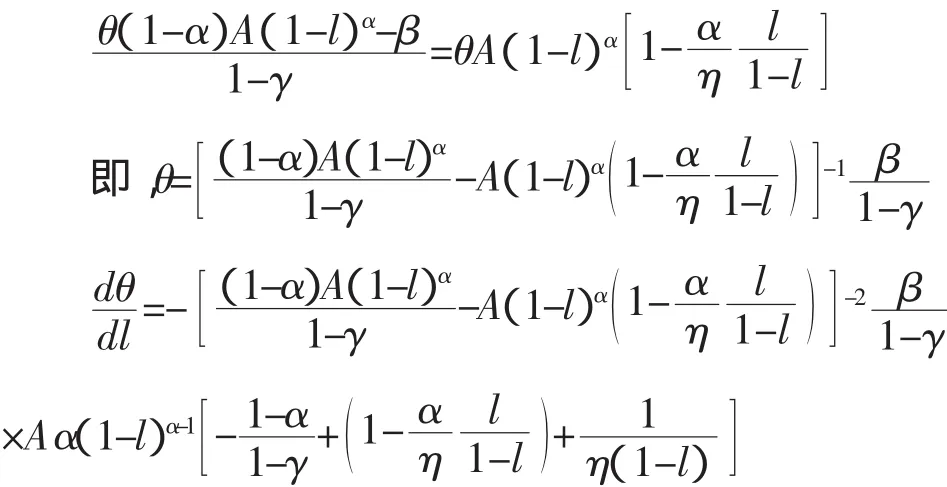
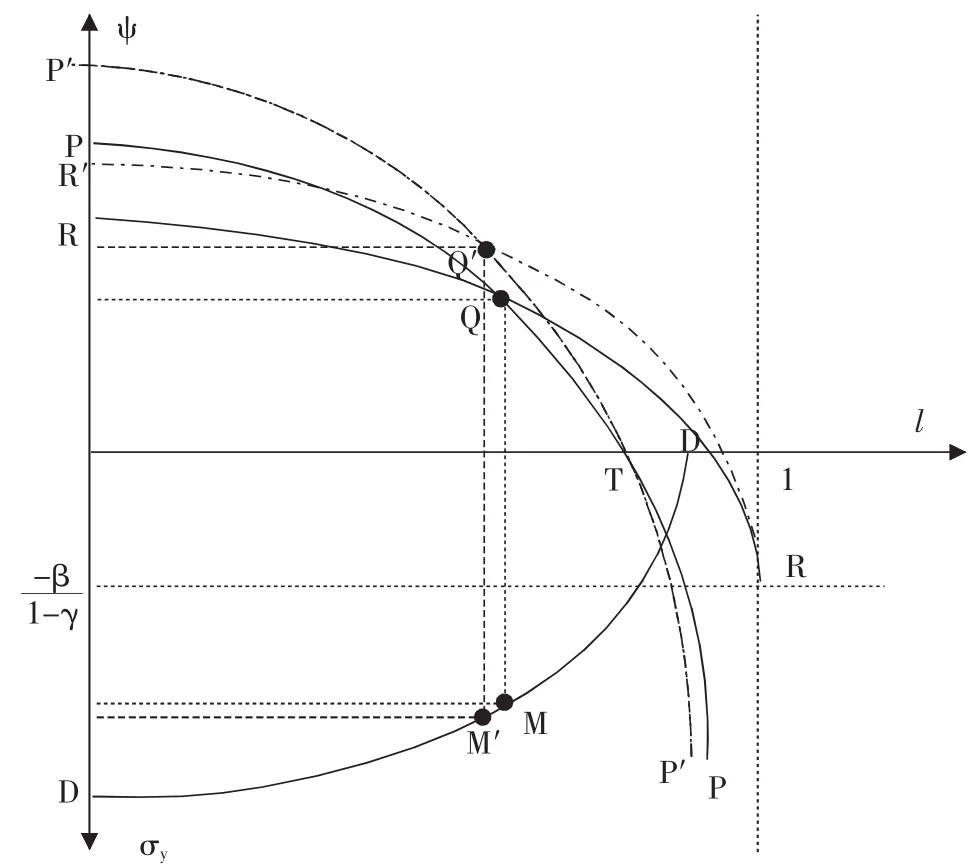
图2 金融效率θ提高对收入不平等的影响

五、结论及评述

本文在Garcia-Penalosa和Turnovsky（2006）研究收入不平等动态演化的内生增长模型框架下，加入金融部门，分析金融效率对收入不平等的影响。模型的结论显示，金融效率的提高会导致更高的经济增长率，但同时也会增加收入不平等程度。金融效率提高会促进经济增长的结论与多数学者的结论相吻合 （比如King and Levine，1993；Levine and Zervos，1998），而金融效率的提高会扩大收入不平等的结论和多数学者实证研究的结论不同。比如，姚耀军（2005）和陈志刚、师文明（2008）等的实证研究均表明，金融效率的提高有助于降低收入不平等。

实证研究结论与理论模型结果不一致的主要原因在于，实证研究中采用的金融效率指标并不是完全反映金融机构将储蓄转化为投资的能力。实证研究中多用储蓄与贷款的比值（FE）来衡量金融中介将储蓄转化为贷款的效率。该指标表面上看起来与本文中衡量金融机构效率的参数θ=I/S相一致，但两者实际上并不一致。实证研究中的金融效率指标（FE）除了受θ的影响之外，还受其他经济变量的影响。比如在θ不变的条件下，人们对未来市场的预期（e）提高，也会促使经济中贷款增加，储蓄减少，从而导致金融效率指标（FE）变化。另外，政府的信贷政策变化同样也会影响到金融效率指标（FE）。因此，实证研究中采用的金融效率指标（FE）并不能真正反映金融机构的效率θ，也就是说实证结论中收入不平等的降低很可能是由影响金融效率指标（FE）的其他经济变量引起的，而不是由金融机构的效率引起的。那么实证研究的结论就很可能与理论模型的结果不一致。

事实上，金融效率的提高会拉大收入不平等程度也不足为奇。首先从市场因素的层面来看，金融部门也是以追求利润最大化为目标，因此它在将储蓄转化为投资时是有选择性的。金融部门会更愿意将钱贷给收益率更高的部门，比如现代部门或者朝阳产业，这会在部门之间或者产业之间造成金融资源的分配不均，从而产生收入分配差距问题。金融效率的提高虽然会增加全社会的总体投资，但同时也会加剧部门之间或者产业之间的金融资源分配不均。高收益、高收入部门会获得更多的投资，这些部门会得到更好更快地发展，这些部门的收入相应地也会提高得更快，从而进一步加剧收入不平等程度。

其次从人为因素的层面来看，在很多发展中国家，比如中国，金融体系还存在一定程度的信贷配给问题。这些国家的金融部门在分配资源时倾斜于国有工业部门（Park and Sehrt，2001），传统农业部门因得不到足够的融资而生产萎缩、收入下降，从而导致收入分配差距的不断扩大。金融效率的提高虽然也能在一定程度上增加传统农业部门的投资，但是相对于国有工业部门而言，传统部门的投资增加幅度远远小于国有工业部门。由于收入不平等程度扩大是由这种人为的金融资源的配置不公造成的，所以金融效率的提高只会进一步加剧这种收入不平等扩大的趋势。

从上述分析中我们可以看出，一味强调金融发展效率层面上的提高而忽视公平层面上的金融资源均衡配置，虽然会提高经济增长率，但也会加剧经济中的收入不平等程度。因此，政府在金融发展问题上，应当兼顾效率与公平。金融资源的配置不公从本质上讲是一种市场失灵，政府有责任对市场失灵进行干预。国家在进行金融改革，提高金融效率的同时，还应该采取积极的金融政策引导金融资源的公平配置。首先，“嫌贫爱富”是金融的天性，无可非议，但金融机构在谋取利润最大化的同时也要承担社会责任，政府要思考如何调动各类金融机构投入弱势群体和弱势部门的积极性和责任心，而且这种调动还必须是可持续的，是讲效率的。其次，消除金融信贷配给，努力引导金融部门对传统部门的资金投入，改善其融资条件，促进其产业结构升级，从而增加低收入人群的收入。最后，要建立普惠性的金融体系，保证社会每个经济主体金融权利的平等。真正有效率的金融体系应该具有包容性，即要普遍惠及一切需要金融服务的社会群体，尤其应惠及被金融体系所忽视的贫困群体。

注释：

①虽然为了方便起见，我们使用Cobb-Douglas生产函数，但是Cobb-Douglas生产函数的使用实际上并且没有放松约束。如果我们将生产函数（1）一般化为Yj=F（LjK，Kj），其中F是两个自变量LjK和Kj的一阶齐次函数，那么我们所有的分析结果继续成立。

②凭直觉，在一个增长经济中，如果劳动供给是固定的，那么更高的劳动收入由更高的资本回报影响，而如果资本随着产出一样的速率增长，那么资本的回报保持不变。

③（7）式中的参数约束是为了保证效用函数是凹函数。

④在平衡增长路径上，θ˙/θ是一个常数，因此可以对（13）式进行加总。

⑤参见Turnovsky，S.J.，2000，“Fiscal Policy，Elastic Labor Supply， and endogenous Growth，” Journal of Monetary Economics，45，185-210。

⑥如果不考虑劳动收入，那么后来的条件就会变为众所周知的C/K＞0。

⑦即由K˙i=0推出的表达式。

⑧PP曲线和RR曲线的性质如下：

我们分别对（35）式和（36）式进行求导，可以得到：

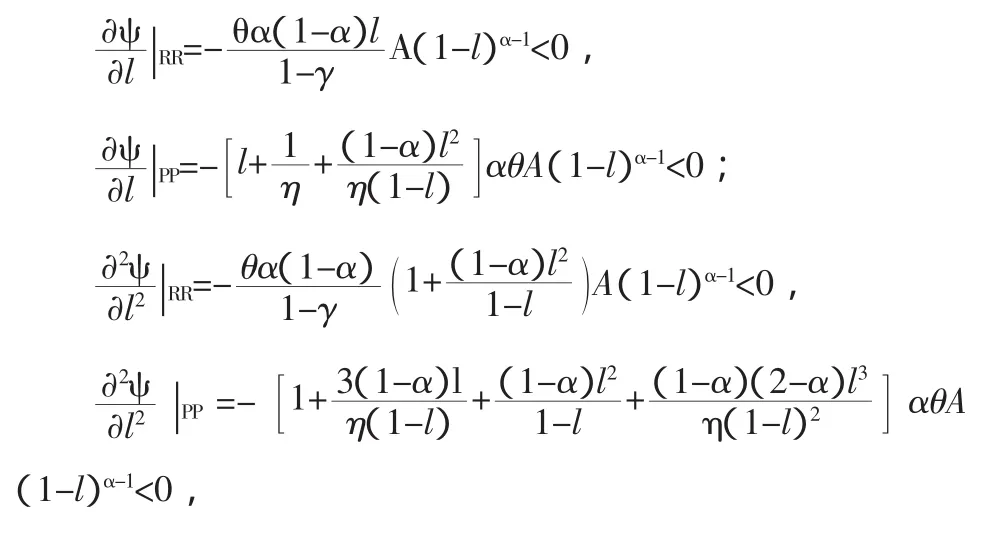
根据上面四个式子我们可以得到，PP曲线和RR曲线都是l的递减函数，并且是凹函数。

另外，我们还可以得到：

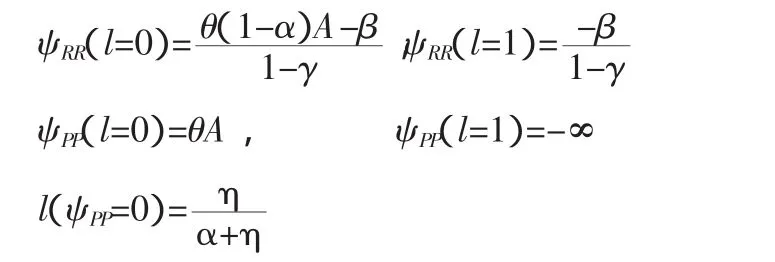
根据上面五个点和PP曲线与RR曲线的性质可以在图1中画出它们的图形。

⑨ρ（l）＜1可以直接由（41）式中的定义得到。可以直接证明，如果均衡是正增长的，（37）式将保证ρ（l）＞1。我们还应该注意到，政策制定者可以设定税率使得为零，如果他希望所有个体都具有相同的税前收入。但是，这会要求一个负的均衡增长率以抵消初始资本禀赋的差异。

⑩DD曲线反映了资本禀赋差异、劳动（休闲）时间和收入差异之间的关系，从直观上看似乎不合常理。在资本禀赋差异固定的情况下，休闲时间越少（劳动时间越长），收入不平等的程度反而越大。西南财经大学的钱龙博士据此提出异议，他认为这说明了资本的初始禀赋决定个人的收入水平，人们不可能通过勤劳致富，反而会适得其反。但是这里需要注意的是，DD曲线中l的表示的不是个人休闲时间，而是全社会的休闲时间，个人的休闲时间是用li表示的。DD曲线的真正含义应该是，在资本禀赋差异固定的情况下，如果全社会的休闲时间越少（劳动时间越长），社会的收入差异就会越大。因为全社会所需的劳动时间越多（休闲时间越少），个人在劳动时间上的分配差异就会越大（无论是自愿的还是人为的），劳动时间的分配差异最终会反映在收入水平上，那些劳动时间长的人可能就会获得更高的收入，社会的收入差异就会增大。

［1］陈志刚.如何度量金融指标——兼论金融发展理论与实证研究的分歧［J］.上海经济研究，2006，（7）.

［2］姚耀军.金融发展、城市化与城乡收入差距——协整分析及其Granger因果检验［J］.中国农村观察，2005，（2）.

［3］陈志刚，师文明.金融发展、人力资本和城乡收入差距——基于中国分省面板数据的实证研究［J］.中南民族大学学报（人文社会科学版），2008，（2）.