斜拉索参数共振新型减振措施

毕继红，尹元彪，王青太

斜拉索参数共振新型减振措施

毕继红1,2，尹元彪3，王青太1

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；3. 新纪元综合咨询公司，东京 12500611)

针对斜拉桥拉索发生的大幅参数振动，提出了一种的减振措施——限位装置．运用有限元方法，建立了单索的二维模型，模拟了拉索的大幅参数共振现象，所得结果与以往研究者得到的解析结果及试验现象相一致，在数值模型中，模拟了限位装置，研究了其对拉索参数共振的抑制作用．从能量原理和参数共振发生机理两个角度，阐明了限位装置的减振机理．在此基础上，讨论了限位装置参数对减振效果的影响．结果表明：限位装置可以显著减小拉索参数共振的振幅；限位装置减振机理明确，能从根本上抑制大幅参数共振的发生；减小限位高度或将限位位置向拉索中间靠拢，会使减振效果更加明显，此结论对限位装置应用于实际工程中有一定的指导意义．

斜拉索；参数振动；限位装置；减振效果

在实际工程中，对已建和在建斜拉桥的观测表明，在无风或风速很小的情况下，个别拉索有时会发生十分剧烈的振动．如著名的法国布鲁东桥、日本名港西大桥等，拉索振幅甚至大到使相邻拉索发生碰撞的程度[1]．在我国的多座斜拉桥中也都观察到拉索的大幅振动．1982年Kovacs第一次用参数激励(一种自激振动)来说明拉索在低风速区发生大幅振动的机理．Lilien等[2]的研究结果表明当桥面振动频率与拉索固有频率的比值接近1或2时，桥面的小幅振动将会引起拉索的大幅振动．国内的学者做了相关的研究，得到了有意义的结果．亢站等[3]研究指出，在一定条件下，拉索可能由于桥面振动的激发而发生参数共振现象．魏建东等[4]建立了几何非线性结构一致激励相应分析方法，分析表明：增加斜拉索的阻尼可抑制其振幅，缩小其发生大幅振动的频率范围，但其张力波幅却也相应增加．赵跃宇等[5-6]运用多尺度法分析了斜拉索的参数共振，结果表明：考虑拉索的弯曲刚度使拉索固有频率变大，从而使斜拉索内共振的幅值和拍频都变大；斜拉索的固有频率与外激励参数对斜拉索稳态解的个数及其稳定性都存在直接影响．

笔者针对拉索参数共振产生的大幅振动，提出了一种减振装置．选用了文献[7]中的工程实例，运用ABAQUS非线性有限元分析软件，研究了限位装置的减振效果．阐述了该装置的减振机理；并计算分析了该装置的限位高度和限位位置对减振效果的影响．

1 拉索有限元模型的建立

1.1拉索的建模方法

斜拉索有限元建模主要有3种方法：等效弹性模量法、多段直杆法和曲线索单元法．

等效弹性模量法由Pippard和Chitty于1944年在分析拉杆时提出，后来Ernst等将其引入拉索的建模中．它是用考虑了垂度变换影响的有效弹性模量的直杆代替悬索．

多段直杆法的想法基于基本的微积分思想，这种方法在悬索桥的模拟中早就提了出来．将拉索离散成一串无质量的、铰接的连杆，并且轴向刚度采用Pugsley提出的重力刚度；主缆自重和其他任意荷载集中作用在连杆的节点上．随着连杆数目的增多，这个体系将趋于真实情况．

曲线索单元法将拉索分成一个或多个曲线单元，其单元刚度矩阵由多项式或拉格朗日差值函数通过在公共节点上的连续性来确定．也有些曲线单元从拉索的真实形状(悬链线)出发．

本文中建模采用了多段直杆法，通过合理运用有限元软件的非线性分析能力和一些常见的杆件单元，可以在要求允许的精度范围内模拟拉索的力学行为．

1.2单元的选择

拉索的受力特点是只能承受拉力，不能承受压力，且抗弯刚度可以忽略不计[8]．本文中选择二维2节点的杆单元进行模拟．这种单元只有1个自由度，只能反映轴向力的变化，而初始应力使得杆单元中只有拉应力，且由于初始应力很大，在后续分析中，杆单元中不会出现压应力；此外，2个杆单元之间，只传递轴力，不传递弯矩．这些与拉索的力学特点十分相似，故采用二维2节点的杆单元(Truss单元)模拟拉索，能够反映实际情况．

1.3模型的建立

选取文献[7]中的工程实例，建立拉索的有限元模型，具体条件如下．

(1)材料参数：弹性模量E=210GPa；泊松比μ=0.3；密度ρ=8257.61kg/m3；

(2)边界条件：模型的两端采用铰支座模拟边界条件；

(3)初始条件：预应力σp=504.07MPa；

(4)几何尺寸：拉索长度为L=107.66m；截面面积为S=0.006273m2．

根据前面的分析，本文中采用108个铰接的杆单元模拟拉索．模型示意如图1所示．

图1 拉索模型示意Fig.1 Schematic of stayed-cable model

1.4拉索自振频率的有限元解

运用有限元方法计算得到拉索第一阶至第十阶的频率及振型．可以通过有限元结果与理论解结果的比较，检验模型的精度是否符合要求．

不考虑弯曲刚度时，拉索横向振动的固有频率的解析解[8]为

式中：T为拉索的轴向拉力，N；L为拉索的长度，m；m为拉索单位长度的质量，kg；n为第n阶振型．

将拉索的第一阶至第十阶自振频率的解析解与数值解进行比较，结果见表1．

表1 频率计算结果比较Tab.1 Comparison of frequency calculation results

由计算结果可知，拉索自振频率数值解结果与解析解结果相差很小，可以忽略不计．所以，用108个杆单元对拉索进行模拟，精度满足要求．

2 工程实例分析

建立拉索参数共振模型，如图2所示．设拉索锚固点A处的水平向振动为

采用分离变量法，得到第k阶模态的拉索-桥面非线性耦合振动方程组[7]为

式中：ωq=(K+EAL)M ；qk(t)为拉索第k阶振型坐标．式(3)为一非线性振动方程，存在2种类型的共振：①当ωq=ωk时，即桥面激励频率等于拉索第k阶模态频率，拉索将发生共振通常称为内共振；②当ωq=2ωk时，即桥面激励频率等于2倍的拉索模态频率，拉索将发生参数共振．

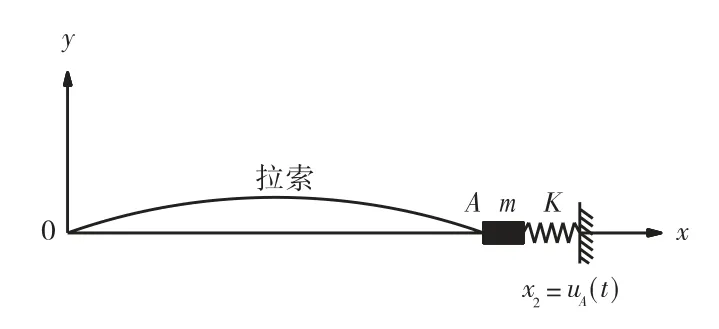
图2 拉索参数共振模型示意Fig.2 Schematic of stayed-cable parametric reso-nance model

建立拉索参数共振的有限元模型．用杆单元模拟拉索，等效桥面质量m用不计几何尺寸的质量点模拟，等效桥面刚度则用一线弹性弹簧模拟．

取m=4×105kg ，K=8.7×107N/m ，k=1(即研究拉索第一阶模态的参数振动)，设初始扰动(即拉索的初始位移)为q1(0)=0.01m，桥面激励为x2= 0.1sinω1t．

建立模型时，如果运用初始条件在单元上直接施加预应力，系统内力平衡后，弹簧的变形会使拉索的预应力损失，同时拉索的长度也会减小，其自振频率将会改变，使得模型与实际的工程实例有较大的差距，从而影响分析的精度与可靠性．为了精确模拟拉索的实际工作状态，本文中采用位移加载法，施加索单元的预应力．

建模时初始状态为无内力状态，设初始索长为L′，弹簧为原始长度．为了达到实例中的状态，可以用位移加载，使右边的支座产生位移Δ，大小为初始拉索L′在题目给定预应力作用下的伸长量ΔL′与弹簧在拉索预应力作用下的伸长量δ之和，此时，拉索长度变为L．通过上述位移加载，可以精确模拟出拉索的实际工作状态．具体计算过程如下.

拉索的预应力为

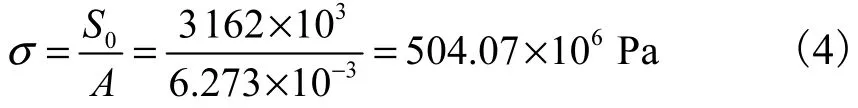
拉索的应变为

则由以上分析得

解得拉索初始长度L′为

弹簧的伸长量为

由此得，拉索右端点的位移为

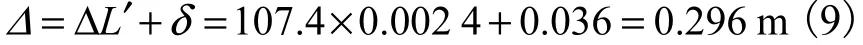
应用位移加载法，具体实施步骤如下.

(1)选用杆单元建立拉索模型，总长度为107.4,m．左端点为固定铰支座．

(2)在拉索右端点处加一质量点m=4×105kg，约束质点的竖向位移，右端点铰接一个刚度为K=8.7×107Nm 的线弹性弹簧，弹簧右端点施加固端约束．

(3)在弹簧的右端点施加位移边界条件Δ=0.296m，经静力分析后体系达到内力平衡状态．

有限元方法分析计算得，加载后拉索的长度为L′=107.662m ，预应力值为σ′=507.1×106Pa，由此可知，通过位移加载法对拉索施加预应力后，模型加载后的状态与题目中给定的初始条件基本一致，精度满足要求．

用以上模型进行动力分析，当不考虑阻尼时，计算得到实例中拉索最大振幅点的振动响应，结果如图3所示．分析结果与文献[7]中的解析解结果基本相同．由此可知，建立的有限元模型可以精确模拟拉索的参数共振现象．

其他条件同上，令桥面激励x2=0.025sinω1t，忽略阻尼作用，计算得到拉索最大振幅点的振动响应，结果如图4所示；考虑阻尼作用，取阻尼比ξ=0.000477，计算得到拉索最大振幅点的振动响应，结果如图5所示．由图可知，当斜拉桥的桥面振动频率与拉索自振频率具有一定的相关性，即使在幅值很小的桥面激励作用下，拉索也会发生大幅参数共振；考虑阻尼作用，拉索的振幅有一定的减小，但是作用不大，并且不会改变拉索大幅参数共振的振动特性．

图3 拉索最大振幅点的振动响应Fig.3 Vibration response of cable's maximum amplitude point

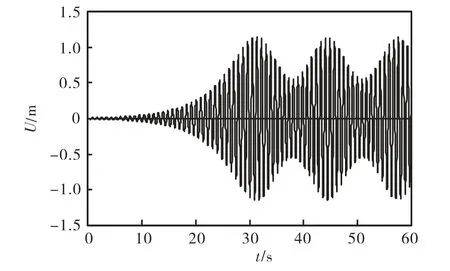
图4 无阻尼时拉索最大振幅点的振动响应Fig.4 Vibration response of cable's maximum amplitude point without damping

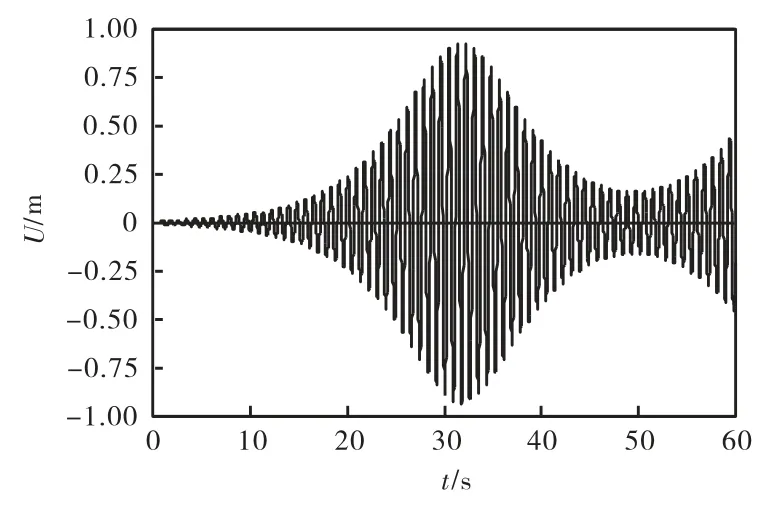
图5 有阻尼时拉索最大振幅点的振动响应Fig.5 Vibration response of cable's maximum amplitude point with damping

3 限位装置的减振研究

3.1限位装置的减振效果

限位装置的作用是限制拉索限位点的振动．其基本参数包括a和l：a是指限位装置的刚性接触面到水平拉索的距离(下文简称间隙)；l是指限位装置安装位置到拉索左端的距离(下文简称限位位置)，如图6所示．使用有限元方法模拟时，可以利用连接单元(connector element)来实现．限位装置的有限元模型如图7所示．给连接单元添加轴向约束，并且施加Stop属性，使得限位点的竖向位移受到上、下限位点的限制，达到模拟限位装置的效果．

图6 限位装置布置示意Fig.6 Schematic of displacement-restriction device

图7 限位装置示意Fig.7 Schematic of finite element model of displacement-Fig.7 restriction device

在图4对应的拉索模型的10 m处加装限位装置，限位高度取a=0.01m,计算得到拉索限位点和最大振幅点的振动响应，结果如图8和图9所示．由图可知，限位点的位移被控制在−0.01～0.01m 的范围内，有限元模型模拟出了限位装置的作用．限位后，拉索的最大振幅有了明显减小，降为原来的110左右，说明限位装置对拉索的大幅参数共振有着明显的抑制作用．

图8 限位点的振动响应Fig.8 Vibration response of displacement-restriction point

3.2 限位装置的减振机理

结构的自振振型具有正交性，其物理意义是：体系按某振型振动时，在振动过程中，其惯性力不会在其他振型上做功．这样，它的能量不会转移到别的振型上去，从而激起其他振型的振动，因此各振型可以单独出现而互不干涉．因此，如果不考虑阻尼的作用，那么结构就没有能量的耗散与转移，按某振动形式一直振动下去．

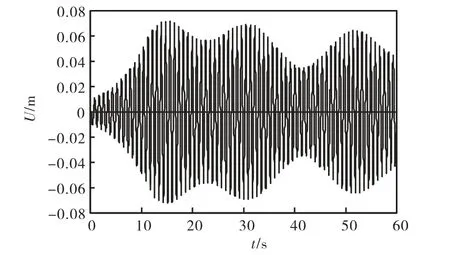
图9 最大振幅点的振动响应Fig.9 Vibration response of the maximum amplitude point

分别对无限位装置和有限位装置2种情况下拉索最大振幅点的振动响应进行FFT分析，得到频谱如图10和图11所示．由结果可知，无限位装置时，拉索发生参数共振，是按其第一阶振型振动；在拉索的某一点处安装限位装置后，当振幅较大时，限位点的振动就会受到限位装置的限制，由此会激起拉索的高阶振型，所以拉索的一部分振动能量就从低阶振型转移到了高阶振型，能量就不会在低阶振型上得到足够的积累，从而抑制了拉索大幅参数共振的发生．

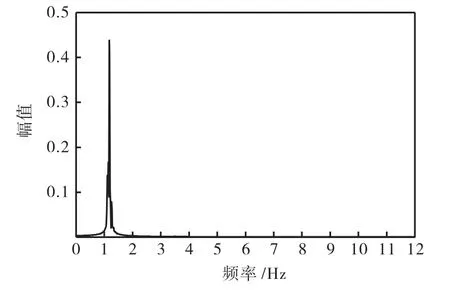
图10 无限位装置时频谱Fig.10 Spectrogram without displacement-restriction de- vice

图11 有限位装置时频谱Fig.11 Spectrogram with displacement-restriction device

此外，对于参数共振来说，发生的必要条件之一是桥面振动频率与拉索自振频率具有相关性，当拉索的振动受到限位装置的影响，拉索的动力特性被改变，就会破坏这种频率的相关性，从根本上抑制了拉索的大幅参数共振．

4 限位装置参数对减振效果的影响

限位装置的主要参数有限位高度和限位位置，本节分别分析了二者对减振效果的影响，得到的结论对该装置应用于实际工程中具有指导意义．

运用有限元方法计算得到，无限位装置时，不考虑阻尼作用，中间节点的振幅A0=1.14m ；考虑阻尼作用，取阻尼比ε=0.000477时，A0=0.93m．由此可见阻尼会对拉索参数共振的幅值产生一定的影响．所以，在研究时，分成无阻尼和有阻尼2种情况进行讨论．

4.1限位高度对减振效果的影响

取桥面激励为x2=0.025sinω1t，限位装置的限位位置L=10m，限位高度a分别取0.01、0.02、0.03、0.04、0.05m，考虑无阻尼和阻尼比为ε=0.000477两种情况，分别计算每个限位高度情况下，拉索振动过程中的最大振幅，计算结果整理成图12和图13．由结果可知，限位装置的减振效果十分明显，不管是否考虑阻尼，限位后，拉索的最大振幅都有了明显的减小．此外，随着限位高度的增加，拉索的最大振幅也线性增加；对数值进行拟合，知两者呈线性关系．根据此规律，通过合理地设计限位高度，能够将拉索的振幅控制在可以接受的范围内．

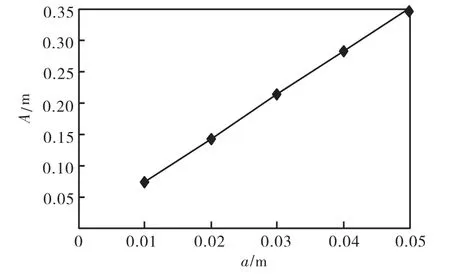
图12 无阻尼时限位高度与最大振幅的关系Fig.12 Relationship between displacement-restriction point height and maximum amplitude without damping

图13 有阻尼时限位高度与最大振幅的关系Fig.13 Relationship between displacement-restriction point height and maximum amplitude with damping

4.2限位位置对减振效果的影响

取桥面激励为x2=0.025sinω1t,限位装置的限位高度a=0.03m,令限位装置的限位位置l(限位装置至拉索端点的距离)分别为10、11、12、13、14、15,m，考虑无阻尼和阻尼比为ε=0.000477,两种情况，分别计算每个限位位置情况下，拉索振动过程中的最大振幅，计算结果整理成图14和图15．由结果可知，无论是否考虑阻尼作用，随着限位位置向拉索中间靠拢，拉索的最大振幅会逐渐减小；对数值进行拟合，知两者呈二次抛物线关系．限位装置应用于实际工程时，应使限位位置尽可能向拉索中间靠拢，但同时要兼顾施工的可行性和建筑美观的要求．所以，建议将限位装置安装位置与拉索端点的距离控制在拉索长度的10%～15%之间．

图14 无阻尼时限位位置与最大振幅的关系Fig.14 Relationship between displacement-restriction point location and maximum amplitude without damping

图15 有阻尼时限位位置与最大振幅的关系Fig.15 Relationship between displacement-restriction point location and maximum amplitude with damping

5 结 论

(1)限位装置可以显著减小拉索参数共振的振幅，减振效果良好．

(2)限位装置减振机理明确，能从根本上抑制大幅参数共振的发生．

(3)减小限位高度或将限位位置向拉索中间靠拢，会使减振效果更加明显．此结论可作为限位装置应用于实际工程时的设计依据．

［1］ Poston R W. Cable-stay conundrum[J]. Civil Engineering，1998，68 (8)：58-61.

［2］ Lilien J L， da Costa Pinto. Vibration amplitudes caused by parametric excitations of cable stayed structures[J]. Journal of Sound and Vibration，1994，174(1)：69-90.

［3］ 亢 战，钟万勰. 斜拉桥参数共振问题的数值研究[J].土木工程学报，1998，31(8)：14-22.

Kang Zhan，Zhong Wanxie. Cable-stayed bridge numerical study of parametric resonance[J]. China Civil Engineering Journal，1998，31(8)：14-22(in Chinese).

［4］ 魏建东，杨佑发，车惠民. 斜拉桥拉索的参数振动有限元分析[J]. 工程力学，2000，17(6)：130-134.

Wei Jiandong，Yang Youfa，Che Huimin. Finite element analysis of cable-stayed bridge cables' parameters vibration[J]. Engineering Mechanics，2000，17(6)：130-134 (in Chinese).

［5］ 赵跃宇，周海兵，金 波，等. 考虑弯曲刚度的斜拉索内共振分析[J]. 湖南大学学报，2007，34(5)：1-5.

Zhao Yueyu，Zhou Haibing，Jin Bo，et al. Considering the bending stiffness of the cable-stayed resonance analysis[J]. Journal of Hunan University，2007，34(5)：1-5(in Chinese).

［6］ 赵跃宇，王 涛，康厚军. 斜拉索主参数共振的稳定性分析[J]. 动力学与控制学报，2008，6(2)：112-117.

Zhao Yueyu，Wang Tao，Kang Houjun. Cable-stayed stability analysis of the main parametric resonance[J]. Journal of Dynamics and Control，2008，6(2)：112-117 (in Chinese).

［7］ 陈政清. 桥梁风工程[M]. 北京：人民交通出版社，2005.

Chen Zhengqing. Bridge Wind Engineering[M]. Beijing：The People's Communications Publishing House，2005(in Chinese).

［8］ Irvine H M. Cable Structures[M]. Cambridge：The MIT Press，1981.

New Countermeasures Against Parametric Resonance of Stayed Cables

BI Ji-hong1,2，YIN Yuan-biao3，WANG Qing-tai1
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China；3. New Era Synthetic Consultants Company Limited，Tokyo 12500611，Japan)

A vibration mitigation device，the displacement-restriction device，has been presented to mitigate parametric resonance of stayed cables. A two dimensional model of the single cable was established with finite element method to simulate the phenomenon of parametric resonance of stayed cables，the results of which were in accordance with previous analytical and experimental results. In the numerical model，displacement-restriction device was simulated and its effect of vibration restriction on parametric resonance of stayed cables was analyzed. Vibration mitigation mechanism of the device proposed was explained with energy theory and mechanism of parametric resonance，based on which the impact of the device parameters on vibration mitigation efficiency was discussed. Study results indicate that the displacement-restriction device can significantly reduce the amplitude of parametric resonance of the cables and prevent large resonance from occurring with clear-cut vibration mitigation mechanism. It is also found that the smaller the gap between the device and the cable，and the farther the device from the end of the cable，the higher the efficiency of vibration mitigation．Such results can offer valuable guidance to application of the displacementrestriction device to real engineering projects.

stayed cable；parametric resonance；displacement-restriction device；vibration mitigation efficiency

O32

A

0493-2137(2010)09-0771-06

2009-04-10；

2009-10-13.

毕继红（1965— ），女，博士，教授．

毕继红，jhbi@sohu.com．