裂隙岩体贯通及锚固止裂路径有限元分析

王 忠 昶， 杨 庆

（1.大连大学 辽宁省高校复杂结构体系灾害预测与防治重点实验室，辽宁 大连116622；2.大连理工大学 土木工程学院，辽宁 大连 116024）

0 引 言

裂隙岩体失稳破坏是由其内部节理裂隙扩展、贯通引起的，而压剪应力场中裂纹在尖端形成的较大塑性破坏区是导致其扩展和贯通引起裂隙岩体破坏的重要原因.国内外学者提出了各种不同的复合型断裂准则，如最大周向（拉）应力判据[1]、最 大 能 量 释 放 率 判 据[2]、最 大 拉 应 变 判据[3]、裂尖径向平面最大应力准则[4]、裂纹尖端塑性区最短距离判据[1]、临界应变准则[5]、偶应力和能量破坏准则[6]等.在裂隙岩体的锚固止裂方面主要有：杨延毅等的等效抹平的加锚岩体的本构方程[7]，李术才等的加锚节理面压剪应力状态下分支裂纹扩展的突变模型[8]，张强勇等的加锚损伤岩体单元[9]，李术才等的锚杆增韧止裂及控制失稳扩展的突变理论模型[10]等.由于裂纹的扩展是因为应力和应变的综合量达到了临界值而发生的，当裂纹尖端区域大范围塑性屈服之后，则应用应变去研究裂纹的扩展.本文将裂隙岩体单元与锚索单元的节点完全重合，应用等效应变与降温法施加锚索单元的预应力，裂纹采用八节点等参单元退化后的奇异单元进行模拟，从应变角度出发，应用塑性区最短距离判据分析不同锚固条件下含两条不同倾角的共线裂纹的裂纹尖端附近的最短塑性区距离、裂纹的扩展方向、裂纹扩展后岩桥之间的有效距离等.

1 裂纹尖端应力场分析和Mises屈服条件

裂纹尖端塑性区的存在是抗裂的重要因素，通常平面应变条件下的塑性区远比平面应力条件下的塑性区要小，因此平面应变条件下的裂纹远较平面应力条件下的更容易发生脆断[1].图1给出了平面应变条件下I－II型复合裂纹受力机制，裂纹尖端附近一点O的应力分量可以表示为

式中：a为裂纹尖端与O点之间的距离；β为裂纹尖端和O点的连线与x轴的夹角.

图1 I－II型复合裂纹的受力机制Fig.1 Bearing mechanism of I－II mixed mode crack

当复合裂纹尖端的正应力大于或等于有效屈服应力时，裂纹尖端附近区域将产生塑性区，塑性区的大小可由Mises屈服条件确定.

按Mises屈服条件，八面体上的剪切应力为

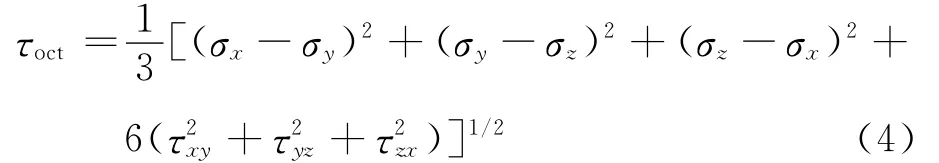
将式（1）～ （3）代入式（4），得O点到裂纹尖端的距离

在复合应力作用下，裂纹沿着其尖端到塑性区边缘最短距离的方向扩展，即可由

的条件确定裂纹的扩展方向β0.

2 预应力锚索的有限元分析

通常假设预应力锚索为线弹性材料，根据锚索的锚固段和自由段受力机制的差异，预应力锚索的锚固段采用杆单元来模拟，锚索的自由段采用两节点线单元来模拟，该单元只有一个自由度，只能承受轴向变形，不允许产生弯矩；当该单元承受单向拉伸变形时，若遭受压力，则单元的刚度矩阵将被忽略，利用这个性质可以模拟钢索类问题.图2为锚索单元的自由段受力示意图.

图2 锚索单元的自由段受力示意图Fig.2 Bearing diagram mechanics of free segment of element of anchor cable

锚索自由段单元的刚度矩阵为

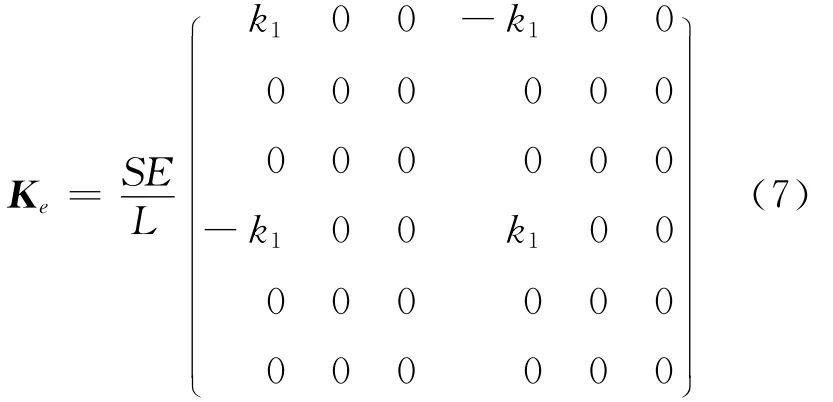
式中：S为锚索单元的截面积；E为锚索的弹性模量；L为锚索单元自由段的长度；k1为单元的刚度系数（压缩为0，拉伸为1）.

锚索自由段单元的应力矩阵为

式中：起始迭代时F为AEεin，随后迭代时F为单元的轴向应力，εin为单元的初始应变；k2为单元的应力刚度系数（压缩为0，拉伸为1）.

锚索单元上施加的预应力矢量为

式中：εT＝αΔT－εin，ΔT＝Tave－Tref，α为温度膨胀系数，Tave为单元的平均温度，Tref为参考温度.

3 不同角度和锚固时两共线裂纹的止裂机理

3.1 岩体及裂纹单元的模拟

平面应变条件下裂隙岩体的尺寸为50 m×60 m，如图3所示.岩体采用八节点平面等参单元，其弹性模量E＝0.30 GPa，泊松比ν＝0.20，粘聚力c＝0.50 MPa，摩擦角 ＝30°.岩体单元的底面施加法向约束，侧面施加水平约束.为了计算裂纹的应力强度因子，在裂纹尖端八节点的平面等参单元退化成1、4、8节点重合的奇异单元，如图4所示.

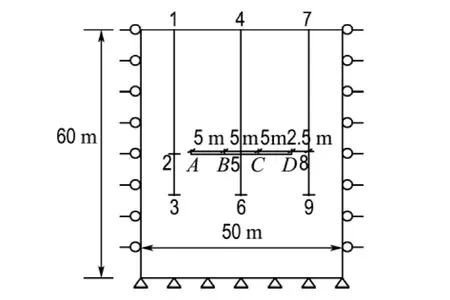
图3 两条共线裂纹（0°）锚固示意图Fig.3 Consolidated sketch of twain collinear cracks of zero degree

图4 等参单元和奇异单元Fig.4 Isoparametric element and singular element

3.2 含裂隙岩体及锚索计算模型的建立

线段AB、CD为两条共线裂纹，长度为5 m，倾角为0°.线段BC相当于完整岩桥，长度为5 m.线段1－3、4－6、7－9为3根长度为40 m 的锚索，其中2－3、5－6、8－9为锚索的自由段，长度为10 m，锚索的内锚固段1－2、4－5、7－8长度为30 m，锚索1－3、7－9与裂纹尖端A、D的距离为2.5 m.以线段AD为直径，以节点5为圆心绘制圆得到倾角为30°、45°、60°、90°的裂纹.单锚条件下只保留图3中的4－6段锚索.通过对比分析不同锚固条件下两条共线裂纹的破坏及扩展路径，获得裂隙岩体的加固止裂机制.

3.3 锚固止裂效果分析

图5、6给出了裂纹倾角不同和锚固条件不同时裂纹尖端B的应力强度因子对比曲线，由图可以看出：

图5 不同倾角和锚固条件时裂尖B的K I对比曲线Fig.5 Contrast curve of K I of B crack tip under different consolidated conditions and angles of crack

图6 不同倾角和锚固条件时裂尖B的K II对比曲线Fig.6 Contrast curve of K II of B crack tip under different consolidated conditions and angles of crack

（1）裂纹倾角为0°～60°时，锚固条件下裂纹尖端的闭合应力强度因子KI比无锚固时的要小，并且随着锚固作用的加强，KI降低越大，此时预应力锚索加固时形成的拉应力区克服了岩体自重形成的压应力.裂纹倾角为90°时，锚固条件下裂纹尖端的KI比无锚固时的要大，随着锚固作用的加强，KI越大，此时锚固相当于增大了裂纹附近的正应力场.

（2）裂纹倾角为30°～90°时，锚固条件下裂纹尖端的KII比无锚固时的小，并且群锚比单锚时的值小，锚索防止裂纹剪切破坏的效应明显；裂纹倾角为0°时，锚固时裂纹尖端的KII比无锚固时的大，且群锚时的值比单锚时的值大，此时锚索加固助长了裂纹的剪切破坏.综合考虑KI与KII的变化趋势，当裂纹倾角为45°、60°时，锚固时的KI与KII下降得明显，此时锚索的加固防剪作用明显.

图7、8给出了裂纹倾角不同和锚固条件不同时裂纹尖端B附近一点的塑性应变εp与剪切应变εt变化曲线，可以看出：

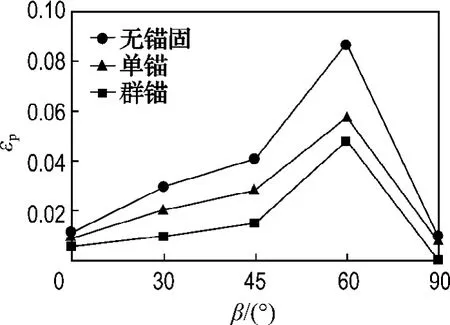
图7 不同倾角和锚固条件时裂尖B附近一点的塑性应变曲线Fig.7 Plastic strain curve of point near B crack tip under different consolidated conditions and angles of crack

图8 不同倾角和锚固条件时裂尖B附近一点的剪切应变曲线Fig.8 Shear strain curve of point near B crack tip under different consolidated conditions and angles of crack

（1）不同锚固条件下裂尖B附近一点塑性应变的变化趋势为随着裂纹倾角的增大而逐渐增大，裂纹倾角为0°～45°时，塑性应变增加缓慢，在45°～60°范围内，其值迅速增加到最大；裂纹倾角为60°～90°时，其值由最大值开始迅速减小到最小.无锚固时该点的塑性应变大于群锚条件下相应的塑性应变，单锚加固时该点的塑性应变介于二者之间，锚固作用削弱了裂纹尖端塑性应变的集中程度，降低了裂尖的破坏扩展几率.

（2）裂纹倾角小于30°时，未锚固条件下裂尖B附近一点的剪切应变随倾角的增大而增大，而锚固条件下剪切应变随倾角的增大而减小，但锚固条件下大于无锚固时的相应值.裂纹倾角为30°～60°时，锚固条件下该点的剪切应变随着裂纹倾角的增大而增大，裂纹倾角为60°时，其值达到最大后开始迅速降到最小.裂纹倾角为30°～70°时，该点的剪切应变随着锚固条件的加强而逐渐减小，此时锚索加固的抗剪效果明显.

表1给出了不同锚固条件下不同倾角的两共线裂纹扩展方向及破裂后岩桥中间的最短距离，由表可知：

（1）在外荷载作用下，相同完整岩桥长度条件下，不同倾角裂纹的分支裂纹扩展后，所得到的完整岩桥的距离是不同的，当裂纹倾角为0°、90°时，即裂纹面与锚固方向水平和垂直时，锚固作用产生的附加应力改变了裂纹尖端的应力场，使得其应力应变场得到了叠加，裂纹尖端附近的塑性区得到加强，得到的最短塑性区距离随着锚固作用的加强而增大，裂纹扩展后岩桥之间的有效距离缩短，锚固效果较其他倾角裂纹的要差，因此在进行锚固设计时，应该合理布置锚固角.

（2）无锚固条件下，裂纹倾角为60°时裂纹尖端塑性区范围最大，由于分支裂纹扩展角度的不同，裂纹倾角为30°时，裂纹扩展后的完整岩桥之间的距离最短.单锚条件下，裂纹倾角为45°时裂纹尖端塑性区范围最大，由于分支裂纹扩展角度的不同，裂纹倾角为60°时，裂纹扩展后的完整岩桥之间的距离最短.群锚条件下，裂纹倾角为30°时裂纹尖端塑性区范围最大，由于分支裂纹扩展角度的不同，裂纹倾角为60°时，裂纹扩展后的完整岩桥之间的距离最短.裂纹倾角为30°～60°时锚固作用使得裂纹尖端的最短塑性区距离减小，岩桥之间的有效距离得到相应提高，随着锚固作用的增强，相同角度的裂纹扩展后岩桥之间的有效距离逐渐增大.

（3）在锚固条件下，裂纹的破坏扩展方向发生了一些变化，但变化不明显；裂纹尖端的最短塑性区距离随着裂纹倾角的增大呈现出先增大后减小的趋势，随着锚固条件的加强，裂纹尖端的最短塑性区距离达到最大值时所需的裂纹倾角越小.相同裂纹倾角条件下裂尖B附近的最短塑性区距离比裂尖C附近的最短塑性区距离要大，说明外荷载越大，裂纹越容易发生破裂.

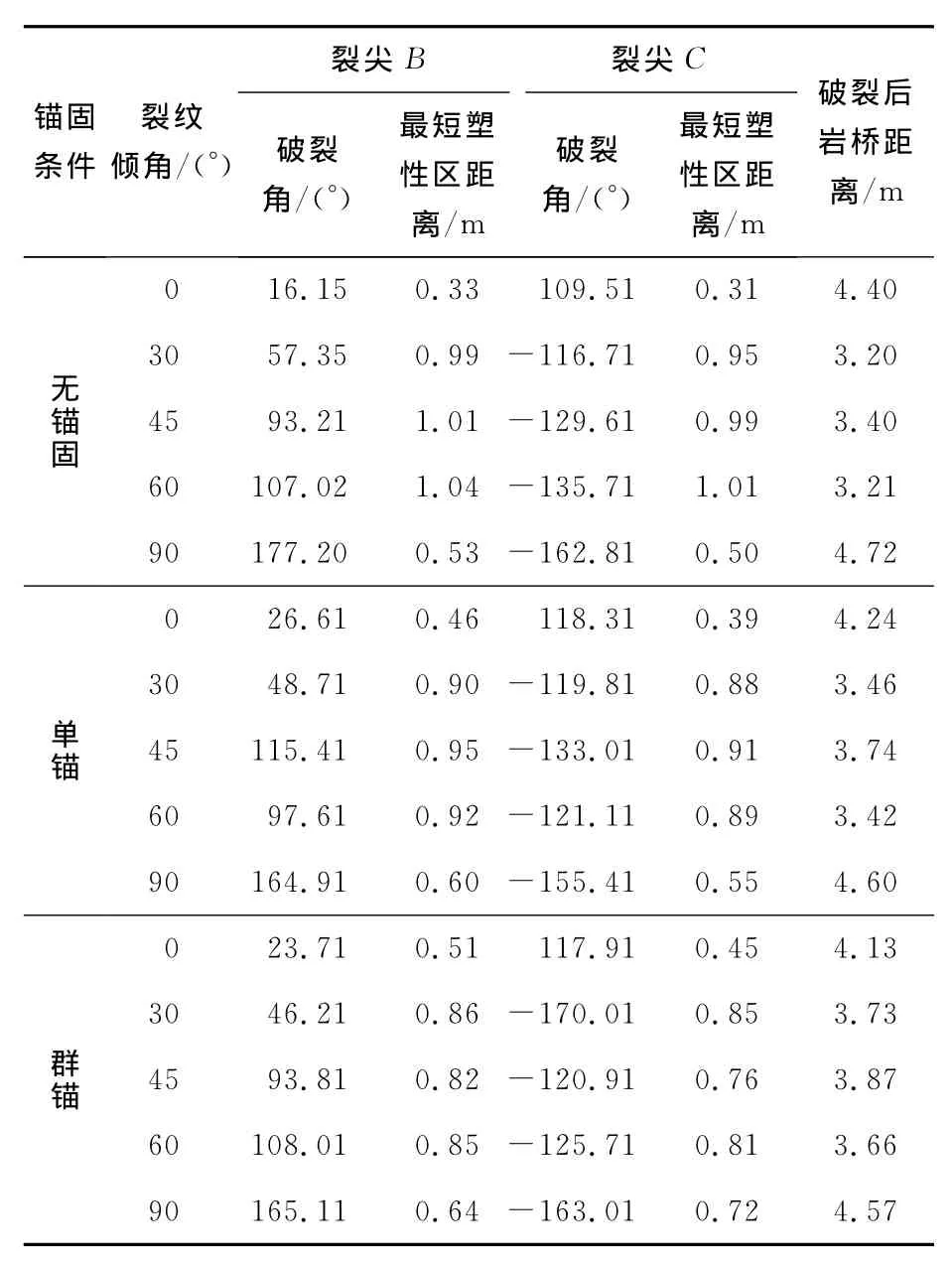
表1 不同倾角和锚固条件时两条共线裂纹扩展方向及贯通统计Tab.1 Statistic of orientation of crack propagation and coalescence of twain collinear cracks of different angles under different consolidated conditions

4 结 论

（1）裂纹倾角为30°～60°时锚固作用使得裂纹尖端的最短塑性区距离减小，岩桥之间的有效距离得到相应提高，随着锚固作用的增强，相同角度的裂纹扩展后岩桥之间的有效距离逐渐增大，阻止或延缓了裂纹的断裂过程，有利于岩体的稳定；相同条件下，群锚时裂纹尖端的最短塑性区距离要小于单锚的；单锚条件下，倾角为45°的裂纹的锚固止裂效果最明显，群锚条件下，倾角为30°的裂纹的锚固止裂作用最明显.

（2）锚固附加应力场使得0°、90°的裂纹附近岩体的正应力或侧向应力得到增加，导致裂纹尖端的最短塑性区距离比相应无锚固时的值大，且群锚时的值要大于单锚时的相应值，此时锚固作用加速了裂纹的扩展，因此在进行锚固设计时，应合理地布置锚固角.

（3）锚固作用使得裂纹的破裂角度发生了一定的改变，但变化趋势不明显；随着锚固条件的加强，裂纹尖端的最短塑性区距离达到最大值时所需的裂纹倾角越小.相同裂纹倾角条件下裂尖B附近的最短塑性区距离比裂尖C附近的最短塑性区距离要大，说明外荷载越大，裂纹越容易发生破裂.但宏观力学克服不了裂纹尖端应力应变的奇异性，因此需要进一步引入含有内部长度变量的微观力学来解决.

[1]尹双增.断裂判据与在混凝土工程中应用[M].1版.北京：科学出版社，1996

[2]许 斌，江见鲸.混凝土 Ⅰ－Ⅱ 复合型断裂判据研究[J].工程力学，1995，12（2）：13－21

[3]董 伟，吴智敏，郑长良.混凝土 Ⅰ－Ⅱ 复合型裂纹断裂准则研究方法概述[J].力学与实践，2006，28（6）：9－14

[4]栾茂田，杨新辉，杨 庆.考虑三向应力效应复合型最大 Mises应力断裂判据[J].岩土力学，2006，27（6）：1647－1652

[5]MCCLINTOCK F A.Ductile fracture instability in shear[J].Journal of Applied Mechanics，1958，10：582－588

[6]CORNETTI P，PUGNO N，CARPINTERI A，etal.Finite fracture mechanics：A coupled stress and energy failure criterion[J].Engineering Fracture Mechanics，2006，73（14）：2021－2033

[7]杨延毅，王慎跃.加锚节理岩体的损伤增韧止裂模型研究[J].岩土工程学报，1995，17（1）：9－17

[8]李术才，陈卫忠，朱维申，等.加锚节理岩体裂纹扩展失稳的突变模型研究[J].岩石力学与工程学报，2003，22（10）：1661－1666

[9]张强勇，朱维申.裂隙岩体损伤锚柱单元支护模型及其应用[J].岩土力学，1998，19（4）：19－24

[10]李术才，王 刚，王书刚，等.加锚断续节理岩体断裂损伤模型在硐室开挖与支护中的应用[J].岩石力学与工程学报，2006，25（8）：1582－1589