一次表面换热器的场协同分析

王 巍， 刘 艳 艳

（大连理工大学 能源与动力学院，辽宁 大连 116024）

0 引 言

1998年过增元从二维边界层的能量方程出发，提出场协同理论.文献[1]中将场协同原理从抛物形流动推广到椭圆形流动，随后文献[2～6]又对二维顺排、叉排板束与平板通道的层流、湍流换热，以及折流杆管壳式换热器、板翅式换热器等进行场协同的实际应用研究，证明了减小速度矢量与温度梯度之间的夹角是强化对流换热的有效措施.

然而，一次表面换热器（primary surface recuperators，PSR）采用了在正弦波纹通道内同一种流体交叉流动的复杂传热方式，因此，场协同理论是否适用，有待于进一步的验证.

为此，本文主要针对一次表面换热器不同的流动交错角和宽高比开展基于场协同理论的计算和分析.

1 层流条件下场协同分析

从二维层流边界层的能量守恒方程

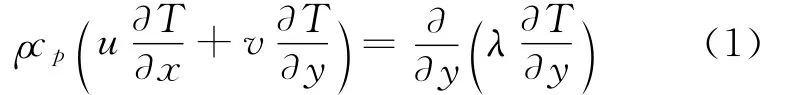
以及导热的守恒方程（忽略x向的导热）

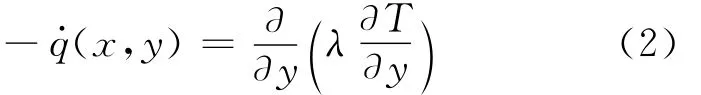
可以获得能量方程的矢量形式：

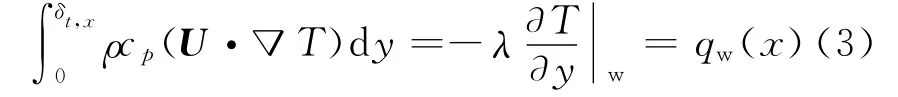
引入量纲一变量

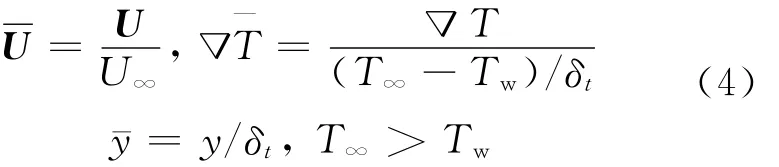
将式（4）代入式（3），进行整理后可得关系式

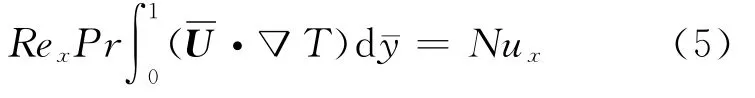
其中Rex、Nux的定义与通常边界层流动分析中的相同.被积因子可写成

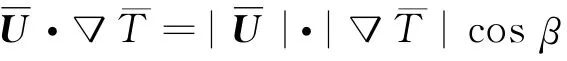
其中β是速度矢量和温度梯度矢量（热流矢量）的夹角.由式（5）知，若想获得最强的传热效果，被积因子应为最大值，在一定的速度和温度梯度下，也即β角为最小值.因此，通过减小速度矢量和温度梯度矢量的夹角，可使对流换热增强.

为了能定量描述和比较不同对流换热情况下的速度场与热流场的协同程度，过增元提出了场协同数的概念.由下式可知，场协同数Fc越大，换热越强.

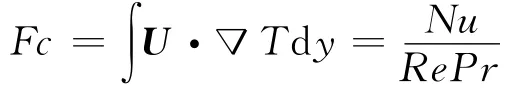
2 物理模型

一次表面换热器是一种模块式结构，尽管其通道数目多达几十万，但除边缘部分，换热器内部微通道的流动和传热特性基本上是相同的，所以，对于这种一次表面换热器的研究多以7×7多元体为模型，以中心单元体为主要研究目标[7]，其基本参数如图1所示[8].形状参数有曲面波长（一个周期）P、波高H（宽高比为P/H）、上下波纹板的交错角θ（即相同两股流体的流动夹角）和壁厚s，W、D表示进口面，E、U表示出口面.

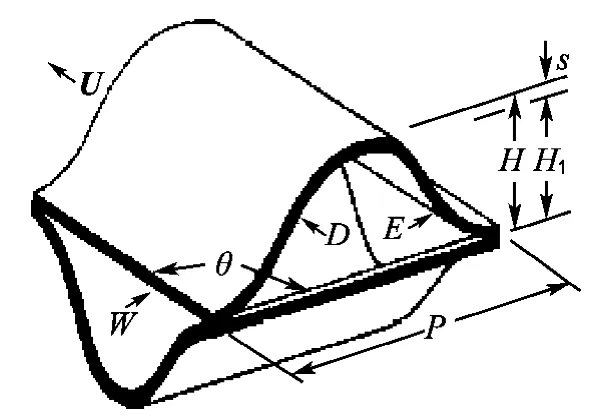
图1 单元控制体Fig.1 Unitary cell

3 协同角的程序编译过程

利用FLUENT内的udf（user defined function），自行编制程序提取速度场与温度场的夹角和全场平均夹角，进一步分析一次表面换热器的换热特性，程序编译过程如图2所示.

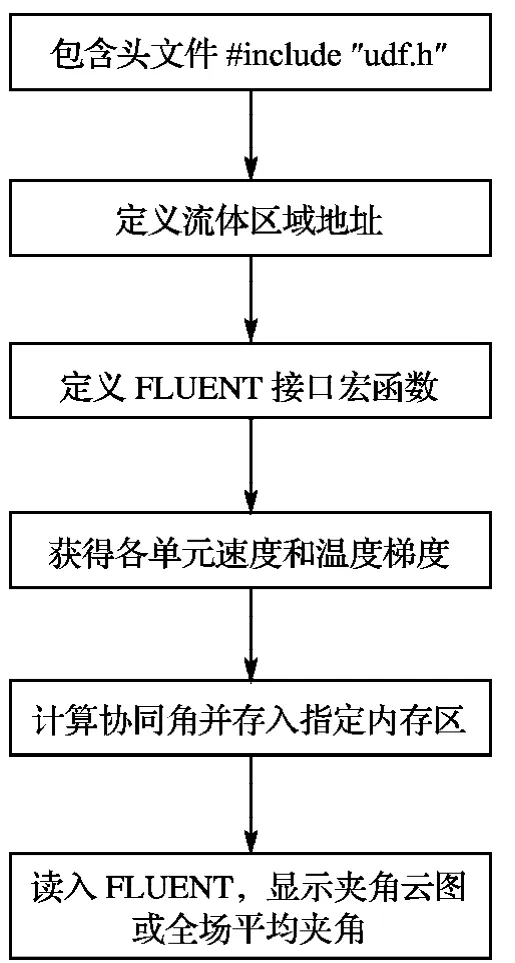
图2 协同角程序编译过程Fig.2 Programming process of the synergy angle

4 计算结果分析

在单元体流动及传热分析中，流体为空气介质，选取质量流量进口，给定流体温度318 K，出口采用静压条件，在固体壁面上取速度无滑移边界条件，设为常壁温300 K[9].

4.1 不同宽高比P/H结构的场协同分析

在流动交错角为60°时，对不同几何尺寸（P/H）的一次表面换热器进行数值计算，并做了场协同分析，结果如图3、4所示.

图3 不同P/H下Nu随Re的变化关系Fig.3 Predicted average Nusselt number as afunction of Re with different P/H

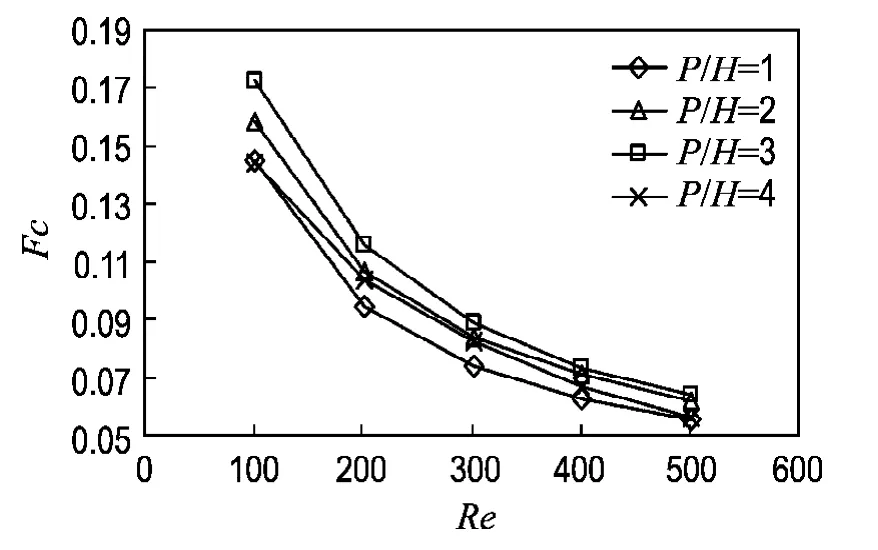
图4 不同P/H下Fc随Re的变化关系Fig.4 Fc as a function of Re with different P/H

由图4可以看出，P/H＝3的协同数Fc最大，说明其速度场与温度场的协同程度最好，换热最强.P/H＝4的协同程度居于P/H＝1和P/H＝2之间，与图3的Nu模拟结果一样.对比图3、4知，在相同雷诺数下，场协同数越大，换热效果也越强.

流体在流动过程中，速度矢量和温度梯度的夹角极大地影响着二者的协同程度，有如下关系式：

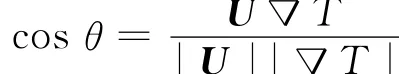
速度矢量U＝U X＋U Y＋U Z；温度梯度而速度矢量和温度梯度在全流场范围内的平均夹角为式中：V i为每一个控制容积的体积，m3；βi为每个节点初速度与温度梯度的夹角.如图5所示.

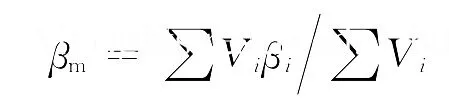
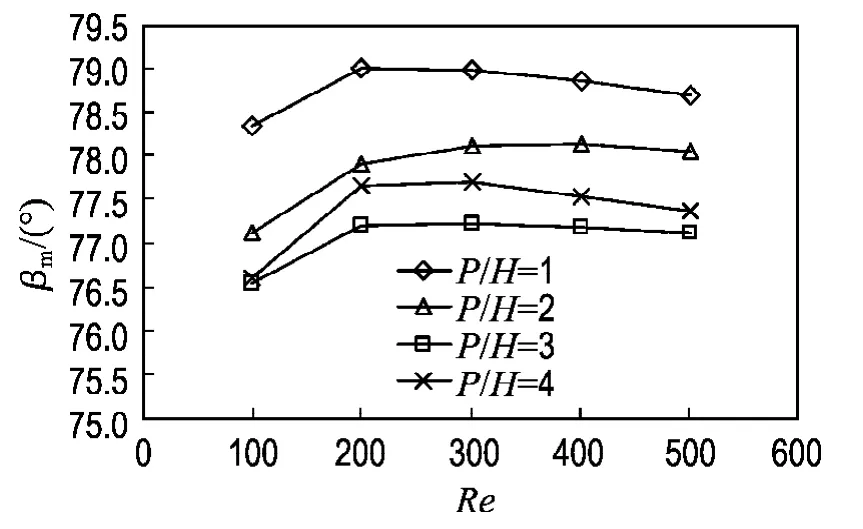
图5 不同P/H下平均协同角随Re的变化情况Fig.5 Average synergy angle as a function of Rewith different P/H

协同角可以反映对流换热的强弱.图5表明，在相同的雷诺数下，P/H＝3时速度矢量和温度梯度平均协同角最小，说明换热效果最好；然而，随着雷诺数的变化，对不同结构尺寸的换热单元，均存在最大的协同角，也就是说，存在着最差的换热状况，因此，在设计交错角为60°的换热器时应避开这一雷诺数范围.这是图3中常规传热分析所不及的.

图6则给出了P/H＝3的单元体中截面协同角等值线图.其中，箭头方向表示进气方向.从中可以看出，随着交错角为60°的两股流体在单元体内的掺混和形成旋涡，流体的速度矢量和温度梯度的夹角将发生变化，协同角在靠近入口和出口侧存在两个最小的区域，并由此向中心不断变化，揭示了该结构单元体对流换热的强弱分布不均匀，为进一步的强化传热提供了结构改进的依据.

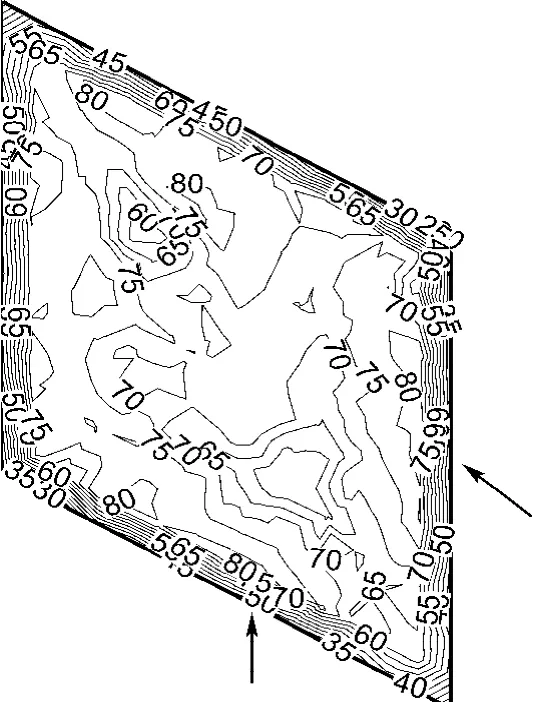
图6 P/H＝3单元体截面协同角等值线图（Re＝100）Fig.6 Synergy angle isoline in the midplane for P/H＝3（Re＝100）

4.2 不同交错角流动的场协同分析

给定单元体宽高比P/H＝3，对不同交错角的单元体内传热特性进行数值计算，并利用协同角完成进一步的分析，结果如图7、8所示.

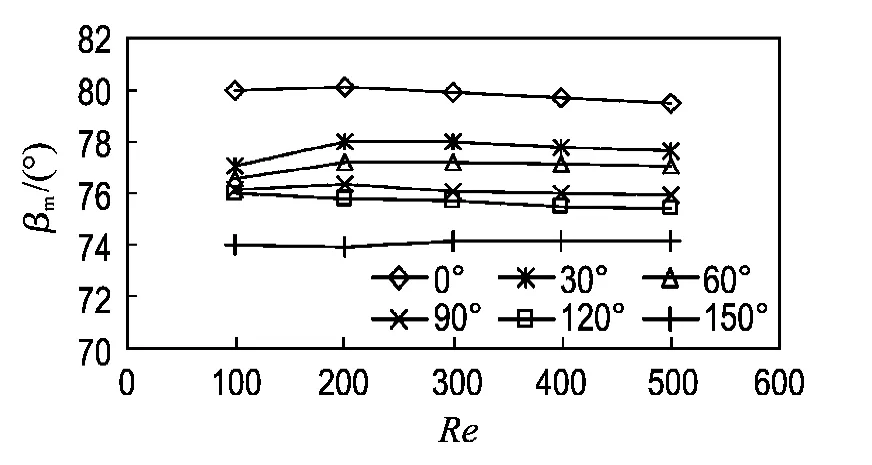
图8 不同交错角下平均协同角随Re变化情况Fig.8 Average synergy angle as a function of Re with different corrugated angles

图7表明，相同雷诺数下，流动交错角度为150°单元体内的努塞尔数最大，换热最强.随着流动交错角度的降低，换热减弱，交错角为0°时换热最差.由图8可知，相同雷诺数下，两股流体以150°交错角流动时，其场协同角最小，此时两股流体的掺混和旋涡形成最强烈，换热效果最强，而直通道（交错角为0°）的流动换热效果最差，与图7的常规传热数值分析相吻合.

图9显示出流动交错角为30°与150°的协同角等值线，通过比较可以看出，流动交错角为150°时场协同角较小，且全场内分布较均匀，换热稳定.然而，由于两股流体的强烈扰动，流动阻力大大增加.图中箭头方向仍表示进气方向.

这些分析与图7计算结果相同，也验证了场协同理论同样适用于分析一次表面换热器的换热特性.

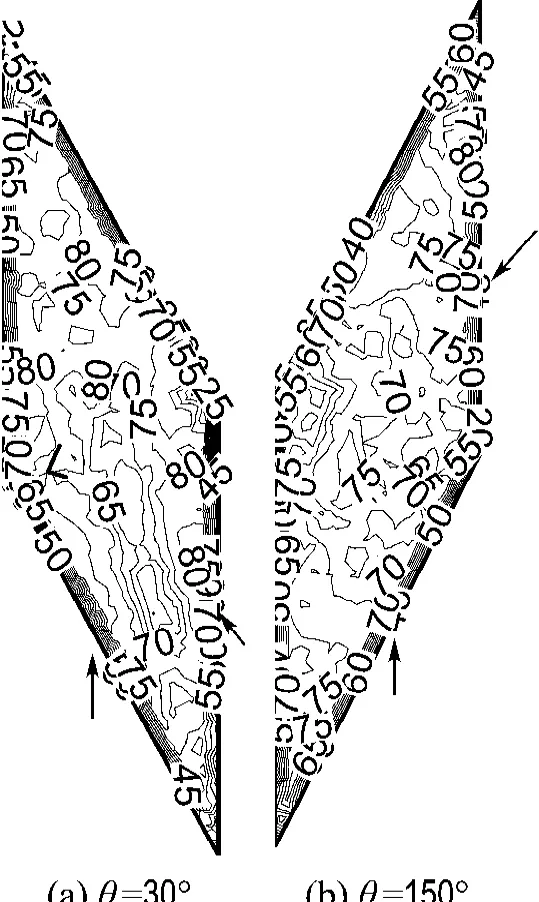
图9 相同P/H 下流动交错角θ为30°与150°的协同角等值线图（Re＝500）Fig.9 Synergy angle isoline in the midplane forθ＝30°and 150°（Re＝500）with the same P/H

5 结 论

本文针对一次表面换热器的复杂单元体结构中流体与壁面的对流换热特性进行了数值分析.利用FLUENT内的udf功能，自行编制程序，着重讨论了在不同的单元体尺寸P/H以及不同的流体流动交错角θ情况下，协同角随雷诺数的变化情况以及全场协同角的分布.计算表明，场协同原理可以用于一次表面换热器的传热分析，并能指导一次表面换热器的换热强化，指明未来结构优化的方向.

[1]王 娴，宋富强，屈治国，等.场协同理论在椭圆形流动中的数值模拟[J].工程热物理学报，2002，23（1）：60－62

[2]过增元，黄素逸.场协同原理与强化传热新技术[M].北京：中国电力出版社，2004

[3]刘 星，王秋旺，何雅玲，等.场协同原理在椭圆形流动中的推广及其应用[J].东北大学学报，2001，22（增刊2）：34－37

[4]过增元.对流换热的物理机制及控制[J].科学通报，2001，45（19）：2118－2122

[5]苏 欣，程新广，孟继安，等.层流场协同方程的验证及其 性 质 [J]. 工 程 热 物 理 学 报，2005，26（2）：289－291

[6]CHEN Ping，DENG Xian－he，DING Xiao－yang，etal.A numerical analysis of thermal characteristics of fully developed turbulent flow with the field synergy theory[J].Journal of South China University of Technology，2003，31（7）：42－47

[7]阴继翔，李国君，丰镇平.交错波纹板原表面换热器通道内对流换热的数值研究[J].西安交通大学学报，2005，39（1）：36－40

[8]CIOFALO M，STASIEK J， COLLINS M W.Investigation of flow and heat transfer in corrugated passages－Ⅱ. Numerical simulations [J].International Journal of Heat and Mass Transfer，1996，39（1）：165－192

[9]STASIEK J，COLLINS M W， CIOFALO M.Investigation of flow and heat transfer in corrugated passages－Ⅰ.Experimental results[J].International Journal of Heat and Mass Transfer，1996，39（1）：149－164