高耸结构建造阶段环境振动测试与模态分析*
2010-06-05陈伟欢吕中荣陈树辉倪一清廖渭扬
陈伟欢 , 吕中荣 , 陈树辉 , 倪一清 , 夏 勇 , 廖渭扬
(1.中山大学应用力学与工程系,广东 广州510275;2.香港理工大学土木及结构工程系,香港)
近十几年来,环境激励(如风荷载)引起的振动响应进行结构模态参数识别的研究一直是土木工程结构系统识别十分活跃的课题,因为其具有不用打断结构的正常使用、无需昂贵的激励设备、只需测定结构的动态响应等特点。环境振动测试的方法不仅已经成功地应用于一些桥梁的动力试验中[1-5],也成功地应用于一些高耸结构的动力试验中[6-9]。
广州新电视塔是广州市新的地标性的重点工程,将于2009年建成。新电视塔的建筑结构(图1)是由一个向上旋转的椭圆形钢外壳变化生成,相对于塔的顶、底部,其腰部纤细。整体结构采用筒中筒结构,通过其外部的钢斜柱、斜撑、环梁和内部的钢筋混凝土筒(截面表现为椭圆形)充分展现了非凡的建筑造型。钢结构外筒包括三种类型的构件:立柱、环梁和斜撑,是主要的垂直承重及抗侧向力结构。其中立柱共有24根,由地下二层柱定位点沿直线至塔体顶部相应的柱定位点,全部采用钢管混凝土组合柱。

图1 广州新电视塔设计图
本文以建造阶段的广州新电视塔为背景,介绍了在一般的自然风作用下的一次环境振动测试,然后用频域分解法和随机子空间法两种不同的方法识别出了测试阶段的前十阶模态频率及相应的振型和阻尼比,并与SAP2000有限元模型的计算结果做了详细的比较。结果表明测试值和理论值低阶模态频率符合得很好,但高阶差异较大。作为此次环境振动测试结果的重要用途之一是利用测试的模态频率和振型来修正电视塔的初始有限元模型,为今后电视塔运营期间的健康监测和损伤检测提供较精确的基准模型;另外还可为高耸结构设计和结构振动控制等提供有价值的模态参数数据。
1 环境振动测试理论
由于采用自然环境激励,故模态参数的识别是仅基于输出的响应的系统识别。目前,国内外研究者提出了各种仅基于输出响应的模态参数识别方法[10],这些方法各自有其缺点,在实际应用中可以多种方法同时使用校核。本文采用两种结构模态识别方法,即基于频域的频域分解法(Frequency Domain Decomposition-FDD)和基于时域的随机子空间法(Stochastic Sub-space Identification-SSI),在专业的振动模态分析软件ARTeMIS Extractor中用这两种方法分别识别出结构的模态参数,即:模态频率、振型和阻尼比。
1.1 频域分解法
频域分解法(Frequency Domain Decomposition)是在传统频域方法(峰值法)的基础上发展出来的[11],该方法仍然假定输入为白噪声,但克服了峰值法的缺点。频域分解法通过对响应谱密度函数矩阵的奇异值分解(SVD),将响应分解为单自由度系统的集合,分解后的每一个元素对应于一个独立的模态。详细的原理阐述可以参考文献[11]。
设x(t)为未知激励,y(t)为结构响应数据,对欠阻尼的结构有下面变换式
(1)
式中:Gxx(jω)为输入的功率谱矩阵;Gyy(jω)为响应的功率谱矩阵;H(jω)为频率响应函数矩阵。上横竿—和T分别表示复共轭和转置。频率响应函数矩阵可以写成下式:
(2)
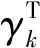

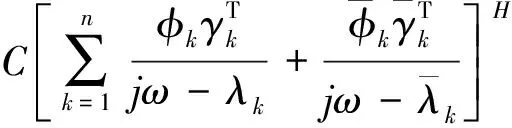
(3)
上标H表示复共轭转置,整理上式可得到下式
(4)
式中k一定时ck为常数;从上面方程估算Gyy(jω)然后对其进行奇异值分解
(5)
其中:Ui=[ui1,ui2,ui3, …,uim],在功率谱密度函数图中,函数的峰值对应结构的特征频率,在某个特征频率ωi附近,该阶模态将起主导作用。如果系统的模态频率分布比较均匀,则功率谱函数在特征频率ωi处的函数值受到某个单一模态的贡献最大,则方程(4)右侧将仅有一项,此时,第一个奇异向量就是模态振型的估计,即振型就是:φ=ui1。如果此特征频率处有多个峰值,表示对应多个模态,则不为零的奇异值对应的奇异向量就是相应的模态振型估计。而阻尼比可以从对应的单自由度相关函数的对数衰减中求得。
1.2 随机子空间法
随机子空间方法(Stochastic Sub-space Identification)自1991年由比利时的Van Overschee和De Moor[12-13]首次提出以来,就成为国内外模态分析方面的专家和学者讨论的一个热点。该方法基于离散时间状态空间方程,是直接处理时间序列的时域方法,适用于环境激励条件下结构模参数的识别。详细的原理阐述可以参考文献[12]。
振动系统的离散状态空间方程可表示为

(6)
式中:xk是离散时间状态向量;A是离散状态矩阵,表示系统的全部动力特性;B是离散输入矩阵;C是输出矩阵,描述内部状态怎样转化到外界的测量值;D是直馈矩阵;wk是处理过程和建模误差引起的噪声,vk是传感器误差引起的噪声,这两种都是不可测量噪声,假设是均值为零的白噪声且互不相关,且满足
(7)
式中:E是数学期望:δ表示Kronecker delta。
对处在环境激励情况的土木结构而言,在实际测量过程中,环境激励是不可测量的随机激励,而且强度基本和噪声影响相似,无法将两者严格区分清楚。因此,将式(6)中的输入项uk和噪声项wk、vk合并得到随机子空间识别的基方程
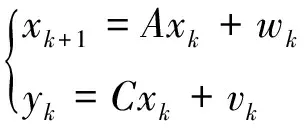
(8)
随机子空间算法的本质是把将来输入的行空间投影到过去输出的行空间上,投影的结果保留了过去的全部信息,并用此来预测未来。随机子空间算法利用线性代数工具(矩阵的QR分解和奇异值分解)从输出数据中获得卡尔曼滤波状态,一旦状态已知,识别问题变成未知系统矩阵的线性最小二乘问题。
2 现场环境振动测试试验
2.1 测试阶段施工状态
截至到2008年5月10日,广州新电视塔核心筒建造至402 m,外筒33环全部安装完毕,34环除2、5、6、8、9和17号钢管柱未安装外,其余均安装完毕。其它建造细节测试人员也作了详细的记录。详细的工况记录便于建立测试阶段的有限元模型,有利于将实测结果与计算结果作对比校核。图2是广州新电视塔测试阶段的实景图和SAP2000有限元模型。

图2 测试阶段实景图和SAP2000模型
2.2 测点布置方案
由于新电视塔的核心筒和外面的钢框架联接成一个有机的整体,在环境振动测试中,测量点全部布置在核心筒内。
在测试中,测量段分为6个截面,分别为32.8, 121.2,173.2,230.4,272和334.3 m,除了截面4(即230.4 m),其他每个截面上布置2个测量点,在截面4上两个测点设置成测量参考点,每个截面的两个测点分别位于核心筒的强电房与弱电房里。本阶段测量的加速度计布置截面平面图如图3所示。
为了充分利用测量加速度计的效率,降低测量的成本,测量时采用分组测量的方法。每个测点测量两个互相正交x和y的水平方向(x和y方向分别为核心筒短轴和长轴方向),传感器安装时保持与欲测量方向一致,同时每次测量各测点的测量方向保持一致,在测点上分别测出x和y方向的加速度响应。对于参考点则同时测量x和y方向的振动响应以保证分组测量具有同步性。
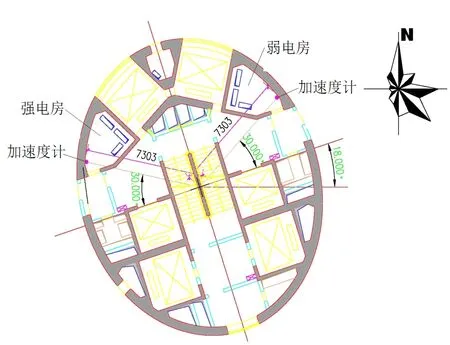
图3 加速度计布置截面平面图
2.3 测试的仪器设备
新电视自振频率较低,建成后的广州新电视塔第一阶频率在0.1 Hz 左右。本次环境振动试验采用日本原产的低频高灵敏的东京测振AS-2000C型加速度计(图4),其测量低频能从0 Hz开始,数据采集的设备必须具有足够的通道数和数据采集精度,而且各通道必须同时采样,无时差。本次试验采用本项目组自行开发的16 位分布式同步采集系统(单台8通道,见图5)。信号传输线采用优质的同轴电缆屏蔽线和网络线。
2.4 现场数据记录
测试时采样频率选用100 Hz,考虑到测量模态阻尼比的需要,每次采样记录时间为两个小时以上。由环境激励产生的加速度响应信号一般都比较弱,图6给出了两个测试方向334.3 m高程某一测点加速度响应的原始纪录。图7给出了334.3 m高程某一测点100 s内的加速度响应纪录,并与作了滤波处理的数据作对比。从100 s滤波后的时程响应上就可以更清晰的看到最低的振动周期大约是5 s,即0.2 Hz左右,另外响应中还含有其他相对高阶频率的成分。进一步分析数据,分别对长轴方向和短轴方向两次测试334.3 m高程弱电房测点加速度响应数据作平均功率谱估计,如图8和图9所示。从谱图上可以看出,测试阶段电视塔的加速度风振相应呈现出密频并且多模态耦合的形态,前几阶模态的贡献是最主要的,但是高阶模态也有一定的贡献。由随机振动理论我们知道,位移响应功率谱等于加速度功率谱除以频率的四次方,由此可进一步推算,对于电视塔目前的风振位移响应,前几阶的贡献是主要的,而对于高阶的贡献几乎可以忽略。

图4 安装好的东京测振AS-2000C型加速度计

图5 数据采集系统
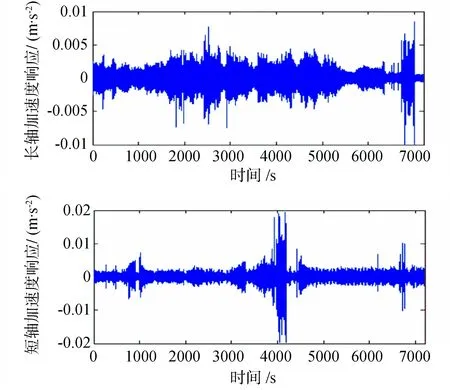
图6 两个小时加速度时程

图8 核心筒长轴平均功率谱

图9 核心筒短轴平均功率谱
3 模态参数识别
用频域分解法和随机子空间法识别的结构模态参数和有限元计算结果归纳于表1中。图10给出了用频域分解法识别过程的功率谱奇异值分解和峰值拾取图。图11给出了用随机子空间法识别过程的稳定图。

图10 奇异值分解与峰值拾取图
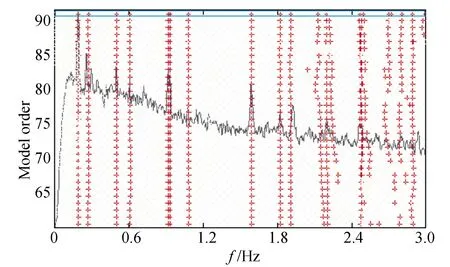
图11 随机子空间稳定图
从表1中首先可以很明显的看出,两种方法识别出的结构频率是基本一致的,而识别的阻尼比则有一定的差异,这是因为一般大型结构的阻尼机制是十分复杂的,包括结构阻尼和气动阻尼,精确的估计是非常困难的。
实测结构动力特性与有限元计算结果的比较,可以通过比较频率和振型的形状来实现。频率的实测结果与有限元计算结果基本吻合,特别是前两阶(以两个方向的弯曲为主),相对误差在2%以内。但高阶的误差相对低阶较大,并且呈现实测结果比有限元计算结果高的规律,这表明有限元分析模型比实际结构的整体刚度要小。
采用模态保证准则(Modal Assurance Criterion),进一步比较实测与计算振型之间的相关性
(9)
式中:{φa}和{φe}分别表示有限元模型计算振型和实测振型向量。一般地,MAC值总是介于0和1之间,MAC值越接近1,表明两者之间的相关性就越好。两种方法识别的实测振型与有限元计算振型的MAC值见图12和图13。可以发现,两种方法大多数的MAC值都较高,这表明了识别的振型与有限元计算振型之间有较好的相关性。总体上看,低阶的相关性要比高阶的好一些,并且随机子空间法识别的振型与计算振型的相关性比频域分解法识别的振型与计算振型的相关性要好一些,但是在第5阶模态及其附近模态的相关性都较差,这是因为第5阶模态和第6阶模态频率非常接近,虽然理论上两种识别方法都能准备的分离密集的模态,但我们发现在实际应用还是有一定局限性,有待进一步的研究。
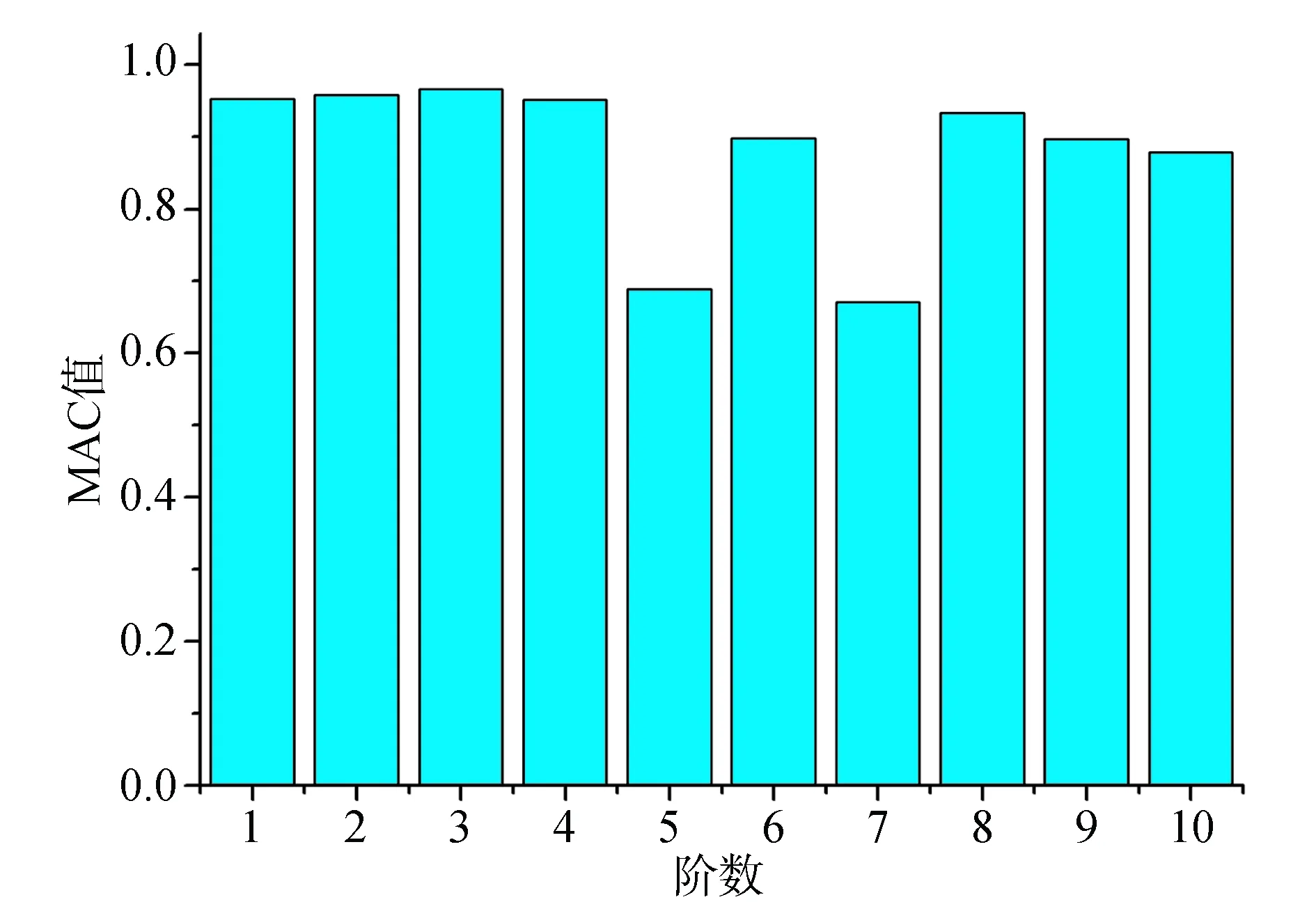
图12 频域分解法与有限元振型MAC值
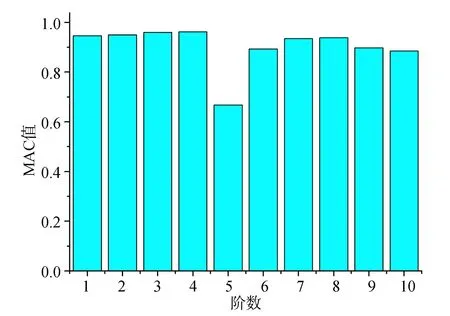
图13 随机子空间法与有限元振型MAC值
最后,限于篇幅这里给出了前两阶有限元计算振型与实测振型(随机子空间法识别)的比较(图14和图15)。前两阶模态以两个不同方向的弯曲为主,两个主要方向并不是完全沿着核心筒长短轴两个方向,而是成一定角度弯曲,大致偏18°和24°左右。
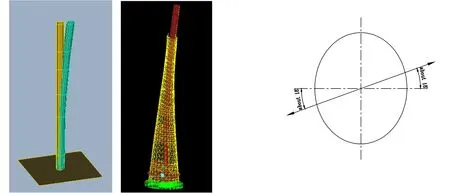
图14 一阶实测振型和有限元振型比较
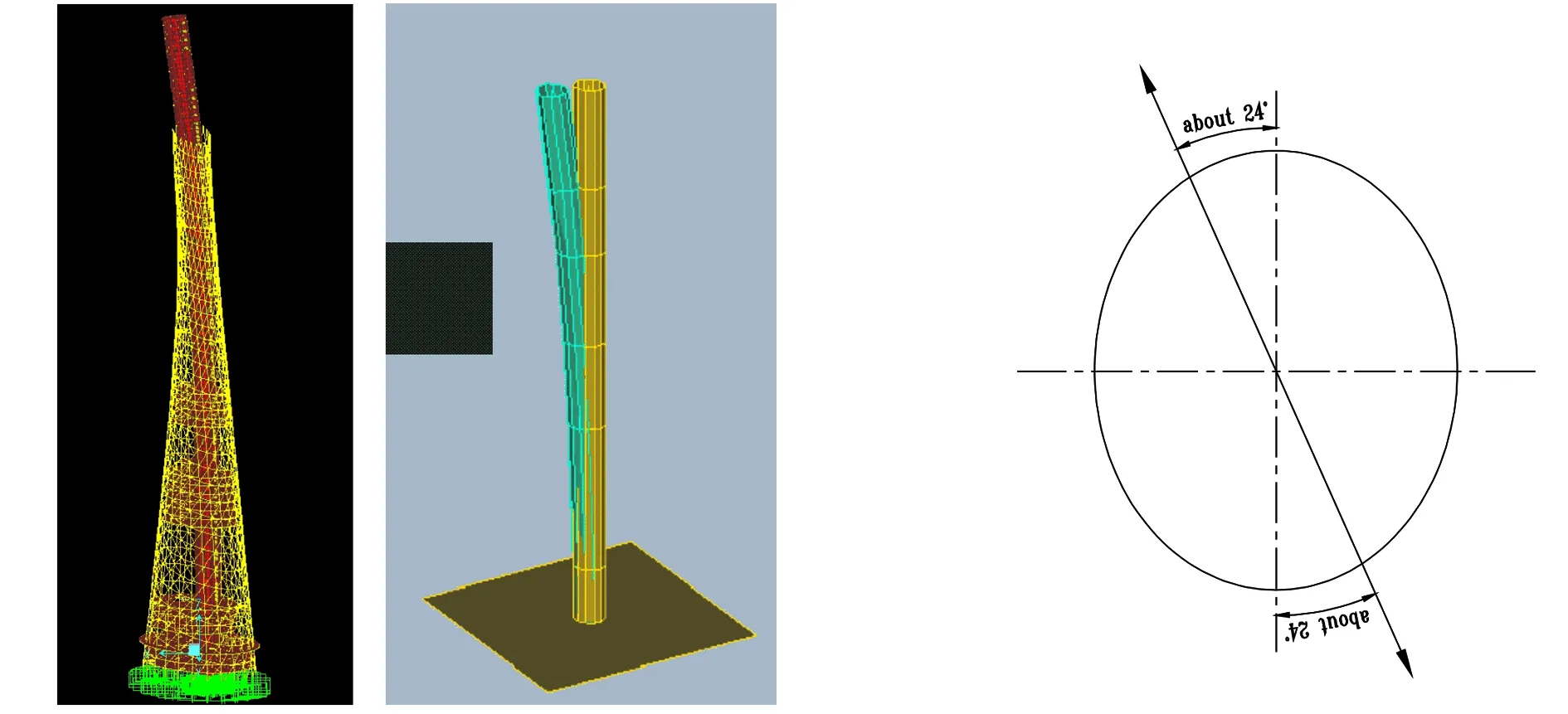
图15 二阶实测振型和有限元振型比较
4 结 论
环境振动法是高耸结构等大型土木结构动力测试的实用方法,并使得结构长期的动力监测成为可能。本文通过对建造过程的广州新电视塔环境振动测试,主要结论有:
1)对于像广州新电视塔这样的超高复杂结构,建造过程的动力测试所得数据是十分珍贵的,一方面,通过测量电视塔在不同建造阶段的模态参数,可以用来逐步地修正电视塔的初始有限元模型,为今后结构运营期间的健康监测和损伤检测提供较精确的基准模型;另一方面,也可以对电视塔结构的减振设计等提供有价值的数据。
2)在完全依靠环境激励(风荷载)的情况下,仅基于加速度响应数据,足以识别出广州新电视塔测试阶段的前十阶模态,包括两个主要弯曲方向的各前四阶模态和扭转的前两阶模态。
3)不同的环境激励可能激发结构的不同模态,新电视塔结构在风激励下的响应以两个主要方向的弯曲为主,测试阶段前两阶频率大约在0.19和0.26 Hz,阻尼比大致都在1.5%。弯曲的两个主要方向并不是完全沿着核心筒长短轴两个方向,而是成一定角度弯曲。实测的结构前10阶频率与振型与SAP2000有限元分析模型计算所得的结果是基本吻合的,特别是前两阶(以两个方向的弯曲为主),相对误差在2%以内。但高阶的误差相对低阶较大,并且呈现实测结果比有限元计算结果偏高的规律,这表明有限元分析模型比实际结构的整体刚度要小,因此结构有限元模型有待行一步修正使得计算的结果更好地与实测结果相符合。
4)本文采用两种不同的方法,即基于频域的频域分解法和基于时域的随机子空间法,两种方法可以实现互补和验证。但两者在识别密集模态时都表现出一定的局限性,随机子空间法较频域分解法要好一些。关于密集模态的识别有待进一步研究。
5)大型高耸结构的阻尼机制是非常复杂的,包括结构阻尼和气动阻尼,精确识别这类结构的阻尼是十分困难的。通过环境振动测试识别结构的阻尼比也有待进一步的研究。
参考文献:
[1] BRINCKER R, FRANDSEN J, ANDERSEN P. Ambient response analysis of the great belt bridge [C]// Proceeding of the 18thIMAC, San Antonio, Texas, 2000.
[2] SHAMA AYMAN A, MANDER JOHN B, CHEN STUART S, et al. Ambient vibration and seismic evaluation of a cantilever truss bridge [J]. Engineering Structures, 2001, 23:1281-1292.
[3] 宗周红, BIJAYA J, 林友勤, 等. 西宁北川河钢管混凝土拱桥的理论和实验模态分析[J]. 铁道学报, 2003, 25(4):89-96.
[4] REN W X, PENG X L. Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration tests [J]. Computers and Structures, 2005, 83:536-550.
[5] GENTILE C, GALLINO N. Ambient vibration testing and structural evaluation of an historic suspension footbridge [J]. Advances in Engineering Software, 2008, 39:356-366.
[6] 张晓志, 于双久. 高耸塔结构动力特性的监测与分析[J]. 地震工程与工程振动, 1999, 19(3):7-14.
[7] BRINCKER R, ANDERSEN P. Ambient response analysis of the heritage court tower building structure [C]//Proceeding of the 18thIMAC, San Antonio, Texas, 2000.
[8] 温瑞智, 周正华, 毛国滨, 等. 应县木塔环境振动试验[J]. 地震工程与工程振动, 2006, 26(4):136-140.
[9] GENTILE C, SAISI A. Ambient vibration testing of historic masonry towers for structural identification and damage assessment[J]. Construction and Building Materials, 2007, 21:1311-1321.
[10] 续秀忠, 华宏星, 陈兆能. 基于环境激励的模态参数辨识方法综述[J]. 振动与冲击, 2002, 21(3): 3-7.
[11] BRINCKER R, ZHANG L, ANDERSEN P. Modal identification from ambient responses using frequency domain decomposition [C]//Proceeding of the 18thIMAC, San Antonio, Texas, 2000.
[12] VAN OVERSCHEE P, DE MOOR B. Subspace identification for linear systems: theory, implementation and applications [M]. Dordrecht : Kluwer Academic Publishers, 1996.
[13] VAN OVERSCHEE P, DE MOOR B. Subspace algorithms for the stochastic identification problem [C]// Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, 1991.
