非紧Riemann流形上一类Kazdan-Warner 型方程光滑解的存在唯一性*
2010-06-05邓义华
邓义华
(衡阳师范学院数学与计算科学系,湖南 衡阳 421008)
在文献[1]中,Kazdan 和Warner 在紧致二维流形上讨论了如下方程
Δw+(hev)ew-c=0
(1)
解的存在性问题。随后,Kazdan等[2],Burago[3],Hulin等[4],Rukmini[5]继续在一些非紧Riemann曲面上讨论了方程(1)。最近,汪悦等[6]在一类非紧高维Riemann流形上研究了方程
Δf+hef-g=0
(2)
并在一定的条件下得到了方程(2)光滑解的存在唯一性。受以上文献的启发,本文主要在一类非紧高维Riemann流形M上讨论如下更一般的Kazdan-Warner 型方程
(3)
其中,λ1,λ2>1为常数,α,β为非零常数,h1,h2,g∈C∞(M)。
方程(3)与Kähler流形上全纯向量丛中Hermitian-Yang-Mills-Higgs度量的存在性有密切的联系[6]。紧致Kähler流形上全纯向量丛中Hermitian-Yang-Mills-Higgs度量的存在性定理首先由Bradlow[7]得到。最近,汪悦等[6]得到了非紧Kähler流形上全纯向量丛中Hermitian-Yang-Mills-Higgs度量的一个存在性定理。设M是非紧Riemann流形,并且满足以下假设:
(A1)M具有有限体积;
(A2)在M上存在非负的穷竭函数φ满足Δφ有界;
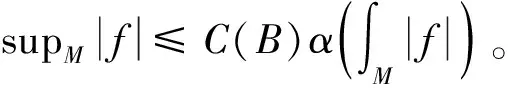
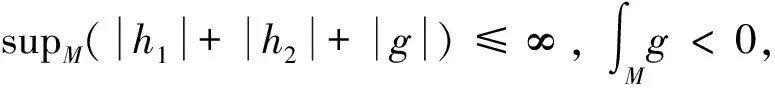
1 一些引理
为了证明定理1,我们需要建立一些引理。在下文中,始终假设
Ma={x∈M|φ(x)≤a}
其中φ是假设(A2)中的穷竭函数,且对于序列a→∞边界∂Ma都是光滑的。考虑Ma上带有Neumann边界条件的热流方程
(4)
这是一个抛物型方程,从而可以得到短时间解的存在性。设f是方程(4)的短时间解,解的存在区间为0≤t 引理1 当αh1,βh2≤0时,带有Neumann边界条件(或Dirichlet边界条件)的热流方程(4)具有长时间解。 证明直接计算可得 由于αh1,βh2≤0,所以 (5) (6) (7) 引理2[9]设φ是假设(A2)中的函数,并且Δφ≤C0。 如果u是定义在Ma×[0,T]的函数满足 设fa(·,t)∈C∞(Ma×[0,+∞))是热流方程(4)的长时间解。下面我们证明M上热流方程 (8) (9) (10) 由引理2,可知对于1≤a0≤a1≤a2,在Ma0×[0,T]上有 (11) 所以对于固定的紧集Z×[0,T],当a→∞时,fa是一Cauchy 序列。类似于文献[6]中命题2.3的讨论,我们有 引理3 设M是满足假设(A1)-(A3)的非紧Riemann流形。若supM(h1|+h2|+g|)<∞和αh1,βh2≤0成立,则热流方程(8)有唯一的长时间解f,且f满足 (12) 类似于文献[6],下面对热流方程(8)的解f(·,t)作一致的C0先验估计。由于λ1,λ2>1并且αh1,βh2≤0,所以 于是, 又因为f|≤ln(ef+e-f)≤ln2ef|=f|+ln2,所以根据假设(A3),我们得到 (13) 引理4 设f是方程(8)的解,则 (14) 证明由文献[6]可知 (15) f(·,t)-f(·,t0)|≤C5(t-t0) (16) (17) 对任意的t0∈[0,+∞),由(15)式、(16)式与(17)式得到 (18) 于是,引理4证明完毕。 (19) 根据(19)式及αh1,βh2≤0得 于是 假设C*>0。 则对任意0<ε 于是对任意x>ε和τ>τ0,有 (20) 另一方面,对x≤ε,(20)式显然成立。于是对充分大的i,有 (21) 从而由(19)和(21)得 (22) 由引理5和(13)式可知存在一正常数C7>0,使得对所有的t,有 于是,由椭圆正则性理论可知f∞是方程(3)的光滑解。定理1证明完毕。 参考文献: [1] KAZDAN J L, WARNER F W. Curvature functions for compact 2-manifolds[J]. Ann of Math, 1974, 99: 14-47. [2] KAZDAN J L, WARNER F W. Curvature functions for open 2-manifolds[J]. Ann of Math, 1974, 99: 203-219. [3] BURAGO Y D. Existence on a non-compact surface of complete metrics with given curvature[J]. Ukr Geom SB, 1982, 25:8-11. [4] HULIN D, TROYANOV M. Prescribing curvature on open surface[J]. Math Ann, 1992, 283:277-315. [5] RUKMINI D. A complete conformal metric of preassigned negative Gaussian curvature for a punctured hyperbolic Riemannian surface[J]. Proc Indian Acad Sci Math Sci, 2004, 114:141-151. [6] WANG Y, ZHANG X. A class of Kazdan-Warner typed equations on non-compact Riemannian manifolds[J]. Science in China, Series A, 2008, 51(6): 1111-1118. [7] BRADLOW S B. Vortices in holomorphic line bundles over closed Kähler manifolds[J]. Commun Math Phys, 1990, 135: 1-17. [8] HAMILTON R S. Harmonic maps of manifolds with boundary[M]∥Lecture Notes in Math, Vol. 471, New York: Springer, 1975. [9] SIMPSON C T. Constructing variations of Hodge structures using Yang-Mills connections and applications to uniformization[J]. J Amer Math Soc, 1988, 1: 867-918. [10] NI L. Poisson equation and Hermitian-Einstein metrics on holomorphic vector bundles over complete noncompact Kähler manifolds[J]. Indiana Univ Math J, 2002, 3: 679-704. [11] MA L. Gradient estimates for a simple equation on complete non-compact Riemannian manifolds[J]. Journal of Functional Analysis, 2006, 241: 374-382. [12] MA L, LI C, ZHAO L. Monotone solutions to a class of elliptic and diffusion equations[J]. Communications on Pure and Applied Analysis, 2007, 6(1): 237-246.
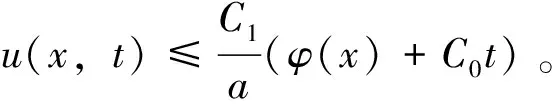
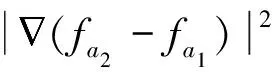
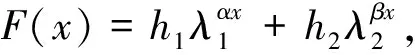

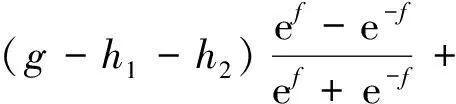
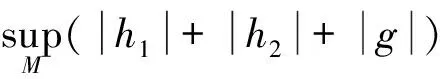

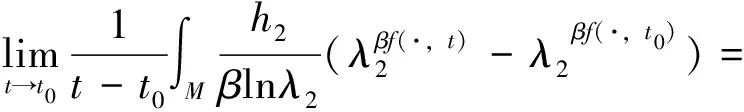
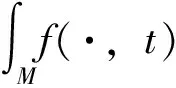
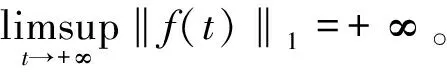

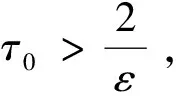

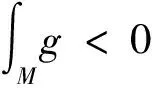
2 定理1的证明

