双层堤基条件下管涌逸出的颗粒流模拟*
2010-06-05游碧波周翠英
游碧波,周翠英
(中山大学工学院∥岩土工程与信息技术研究中心,广东 广州 510275)
管涌问题是水利工程界普遍关注的重要研究课题。根据国内外的研究现状,管涌现象的机理研究主要分为理论解析模型研究、室内外实验研究以及数值模拟等方面。由于管涌问题涉及到水与土颗粒的相互作用,其机理十分复杂,传统的理论模型和实验研究均存在某些局限[1]。随着计算机技术的不断发展和各种数值模拟方法的应用,以数值分析技术模拟渗透变形的发生及其发展过程,成为研究渗透变形问题的一个主要方向。根据现有数值模拟成果,以有限元为代表的连续介质方法在管涌研究中得到了广泛的应用[2~5]。采用连续介质方法模拟管涌时,基本是以渗流场的模拟为基础,将离散的颗粒看成是连续的流体加以研究。连续介质方法依赖高度简化的、规定性质的本构方程而对颗粒物性参数、粒径、形状及其分布等对管涌演化的影响则难以考虑;并且管涌区域的参数在不断变化,连续介质方法对管涌通道及管涌通道过渡区的网格划分问题难以处理,因此只能模拟稳定渗流场的状况。管涌的实质是细颗粒从粗颗粒组成的骨架孔隙中流失,土体颗粒和水流相互作用的力学机制十分复杂,连续介质方法对反映堤基管涌这类颗粒运移引起的模型和参数不断调整的复杂问题,以及实现对管涌发展演化过程的模拟等均存在一定的局限性。
离散单元法与连续介质方法相比,在分析具有离散性质的物质方面表现出了优越性。其基本思想是将不连续体分离成若干离散单元的集合,单元之间无须满足位移连续与变形协调条件,运动方程的迭代采用显式的中心差分格式,速度快,所需空间小,适用于求解大变形和非连续问题[6]。颗粒元方法作为离散元的一种,是专门用来求解固体力学大变形和颗粒流动问题的数值方法,它通过接触方程和运动方程将颗粒之间的复杂的相互作用由计算机来完成,因而可以对土颗粒相互之间的细观作用形象化的表现出来。目前,颗粒元在岩土、矿冶、农业、食品、化工、制药和环境等领域均已广泛地应用[7]。对于水-土相互作用问题,目前已有学者开始采用颗粒元方法对离散颗粒与水的相互作用进行分析研究[8],也有学者开始采用颗粒流程序针对管涌试验进行数值模拟分析,并得出了一些有价值的研究成果[9]。可以看出,以颗粒元为代表的离散元方法,为在细观尺度上解释和分析管涌现象提供了一条途径。
管涌发生时,管涌出口附近地层的颗粒流失将引起管涌的迅速发展,导致管涌通道的形成,甚至发生堤基破坏。对管涌口附近地层的颗粒流失规律、流速分布的分析研究,弄清管涌口附近颗粒流失的规律,对于分析险情、指导抢险,具有重要价值,对于进一步研究管涌演化规律具有重要意义。但在管涌口出现时,第一要务是抢险堵漏,因而难以对管涌口附近地层的相关细观参数进行测量和现场分析,此方面目前尚未见相关研究。本文拟通过颗粒流程序平台PFC2D(Particle Flow Code in Two Dimension),采用流-固耦合的分析模型对管涌口附近的颗粒流失现象进行模拟,并通过FISH语言开发程序,对颗粒流失量、孔隙率、流速等计算结果进行分析。
1 颗粒流基本理论
颗粒流是基于离散元的原理提出的专门用于模拟圆形颗粒介质的运动及其相互作用的一种数值方法[10]。它采用圆盘模型模拟颗粒,通过接触方程和运动方程将颗粒之间的复杂的相互作用由计算机来完成,它除了细观模拟上的优势之外,随着力的平衡过程,土体的宏观运动也可以通过土颗粒的微观运动表示出来。
1.1 基本假设
根据文献[10]中对颗粒流方法的相关阐述,采用颗粒流进行模拟时具有如下基本假设:①颗粒单元为刚性体;②接触发生在很小的范围内,即点接触;③接触特性为柔性接触,接触处允许有一定的“重叠”量;④“重叠”量的大小与接触力有关,与颗粒大小相比,“重叠”量很小;⑤接触处有特殊的粘结强度;⑥颗粒单元为圆盘形(或球形)。
1.2 计算循环过程
颗粒流方法以牛顿第二定律与力—位移定律为基础,对模型进行循环计算。图1给出了计算过程循环图。
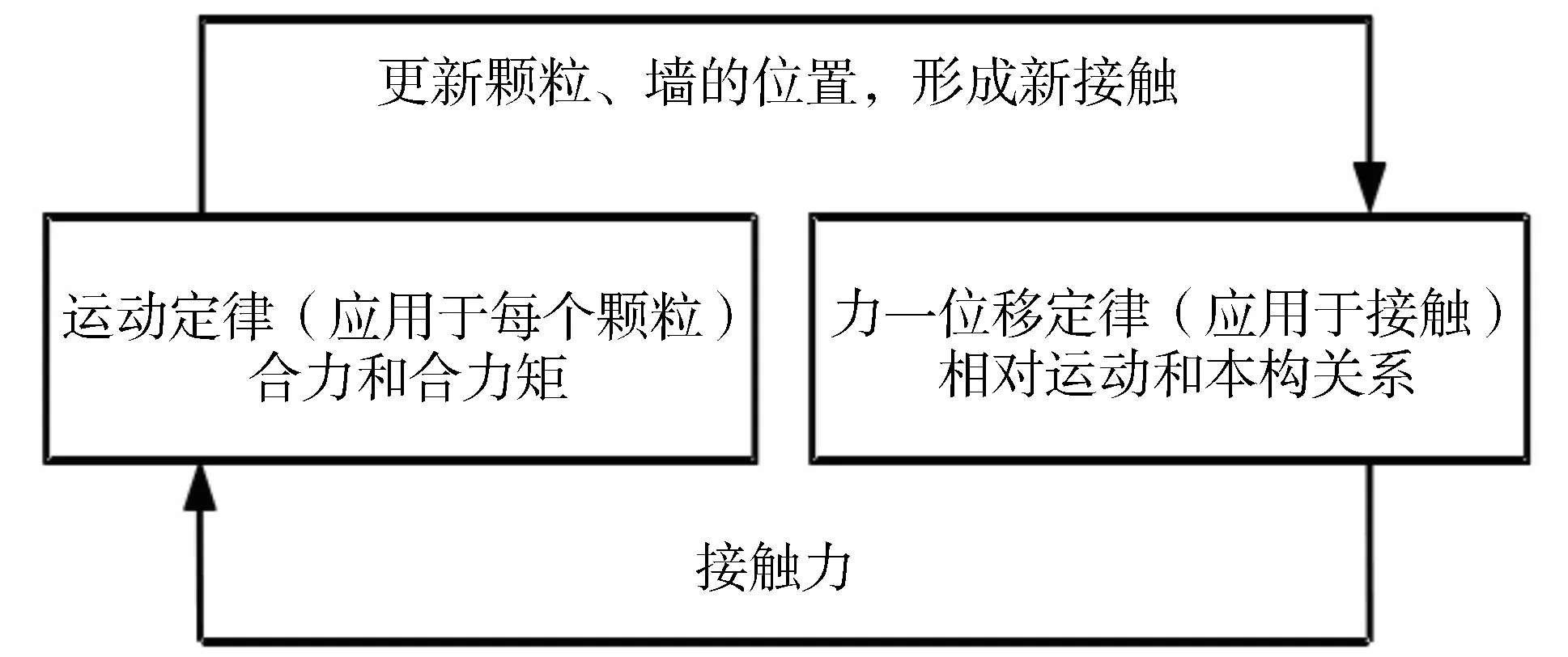
图1 颗粒流计算过程循环图(改自文[10])
PFC2D的计算过程可分为以下4步:①接触检索;②利用接触本构关系计算作用于颗粒上的不平衡力与不平衡力矩;③颗粒满足运动方程(即牛顿第二运动定律);④更新颗粒位置,进行下一步迭代。
1.3 接触模型
对材料本构特性的模拟,PFC2D是通过接触本构模型来实现。每一颗粒的接触本构有:①接触刚度模型;②滑动模型;③粘结模型。接触刚度模型提供了接触力和相对位移的弹性关系;滑动模型则强调切向和法向接触力使得接触颗粒可以发生相对移动;粘结模型是限制总的切向和法向力使得颗粒在粘结强度范围内发生接触,包括接触连接和平行连接[11]。本文的模型在模拟砂性土颗粒之间接触作用时采用接触刚度模型,黏性土颗粒之间采用粘结模型中的平行粘结模型。粘结模型能同时传递力和力矩,发生在接触颗粒间圆形或方形有限范围内,可以描述颗粒之间有限范围内有粘接作用特性,由法向刚度、切向刚度、法向强度、切向强度和连接半径等参数进行定义,相对应的作用力以总接触力与力矩表示。
2 管涌口数值模型的建立
2.1 生成模型
北江大堤位于广东省北部,是防御北江和西江洪水侵袭广州和珠江三角洲地区的重要屏障,是广东省最重要的一条堤防,也是全国确保的七大堤防之一。北江大堤石角段历史上曾多次决堤出险,是北江大堤的主要险段,吸引了一些学者对此段堤基的管涌问题开展相关研究[12-13]。石角堤段的遥堤在0+650断面乐排河闸附近未采取任何防渗措施,堤身、堤基渗透性较大,一旦该堤挡水将存在发生渗透变形的危险[14](其地层断面见图2)。本文基于此管涌危险堤段的地层条件,建立模型,模拟发生管涌时逸出口处的颗粒流失现象。
首先选取模拟对象的范围,考虑计算规模和效率的关系,集中选取该堤基管涌口周围一定范围内的颗粒进行建模。由图2可以看出,堤内地层结构为典型二元堤基,覆盖层为粉质黏土,下面是中粗砂层。据此建立数值模型尺寸为10 m×6 m,其中覆盖粉质黏土层厚度为1 m,下卧透水中粗砂层厚度为5 m,模型在左、右、底侧分别设置PFC2D透水边界墙作为边界条件,以模拟实际的水流边界。
在该尺寸的模型中,如果按实际土颗粒的大小模拟,得到的颗粒数量远远超过百万甚至千万,目前的计算机和软件还无法满足要求。这里,我们关心的是管涌发展的演化机制,而不是为了模拟堤基土的颗粒数量,所以在模拟过程中对土颗粒的尺寸进行了同比放大,同时将堤基简化为双层计算,这样即克服了计算机容量和速度的限制,又能满足计算精度的要求,同时,对模拟该处管涌的规律也有一定的参考意义。颗粒试样尺寸分别为:粉质黏土采用粒径为0.015 m的颗粒,中粗采用粒径为0.05 m的颗粒,编制FISH函数由PFC2D随机生成器生成。颗粒生成的具体过程如下。
首先在墙体所在范围内充满流体,在墙体范围内采用自由下落法生成颗粒,定义颗粒的相关参数和重力加速度,首先生成下层的砂土颗粒,让颗粒在重力作用下达到平衡状态,这样可以消除内部的不平衡力;待颗粒静止后,删除多余颗粒,再用同样方法生成上层黏土颗粒,此时土体状态即为模型初始状态。这种颗粒生成方法的优点是可以保证试样生成过程中颗粒通过相互作用不断调整,较易达到自然受力平衡;最后在黏土层的中间部位,删除宽度为0.1 m的颗粒带,以模拟管涌口。最终生成的模型颗粒总数约为12 500个,模型如图3所示。

图2 石角遥堤(乐排河闸)0+650断面图
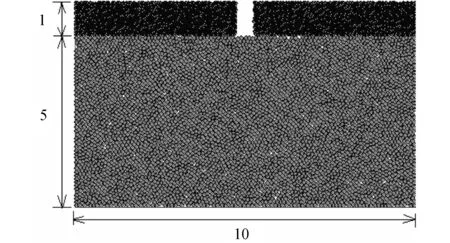
图3 管涌口数值模型
2.2 参数的选取
砂土颗粒采用接触刚度模型,黏土颗粒采用平行粘结接触模型。本文的数值模拟强调的是颗粒的运移规律与实际情况相近。
因此,在建立实际工程模型之前,先构造并运行简化的测试模型,并设置流体,在左侧和下侧施加水头,模拟在实际的水力边界条件,颗粒在水压力下发生起动,反复调整颗粒相关参数,使得数值模型与实际管涌具有大致相同的颗粒起动条件。粉质黏土覆盖层参数的确定参考前人试验中通过建立模型进行粘接力试验确定,这样,可保证其粘结刚度与实际情况接近。颗粒相关参数如表1所示。
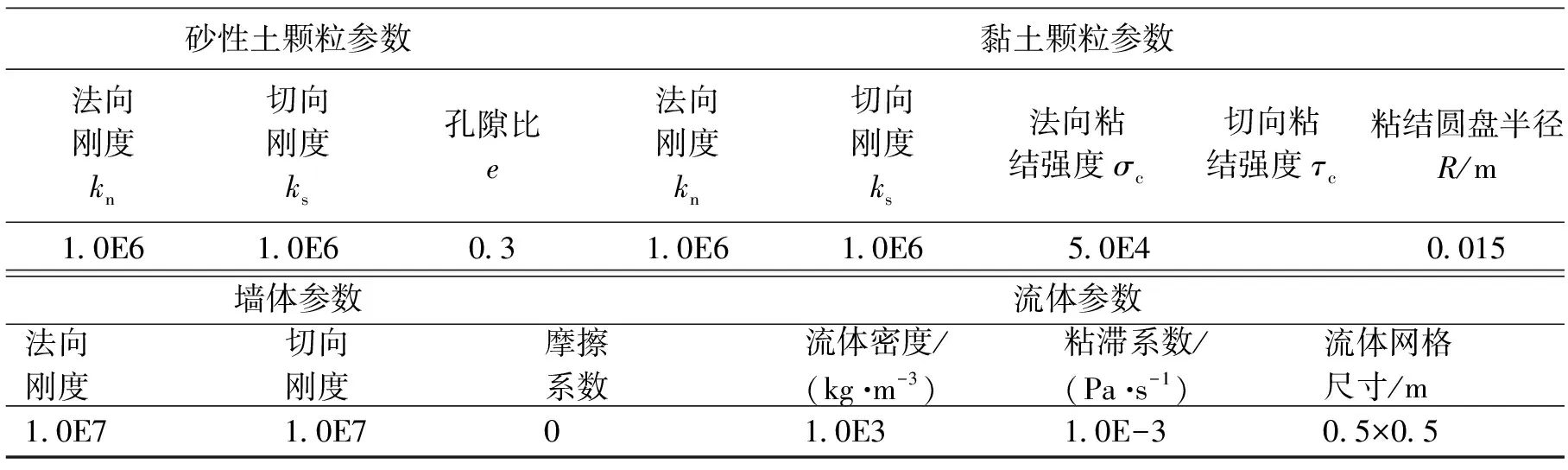
表1 颗粒流模型细观参数表
需要指出的是数值模型采用的各项参数,如刚度、摩擦系数、平行粘结的各项指标并非真实堤基土的物理指标,而仅仅是颗粒流数值模拟的自定义指标,与真实土层物理指标没有直接的关系,而且迄今还没有能从细观力学指标反应宏观力学指标的关系公式。本文参数取值遵循颗粒流数值模拟的基本途径:首先构建并运行简化模型,这样可对力学细观的概念有深入的了解,通过这种前期简化模型的运行,可得计算模型的几何参数及初始条件,分析简化模型的结果,将其与实测结果或宏观现象进行对比,大致确定出各参数的取值范围,一般还需加以修改,多次试算即可得出计算参数的取值。
3 计算结果分析
在模拟墙体上施加压力差,形成向右向上的水流压力,在程序中设置测量圈和内置函数来求取颗粒的孔隙率和渗透率指标,测量圈的设置如图4所示。并编写了试样各个部分的流体cell孔隙率的FISH函数,用来记录管涌口附近孔隙率及水流流速的变化规律,以下对模拟的结果进行详细讨论和分析。
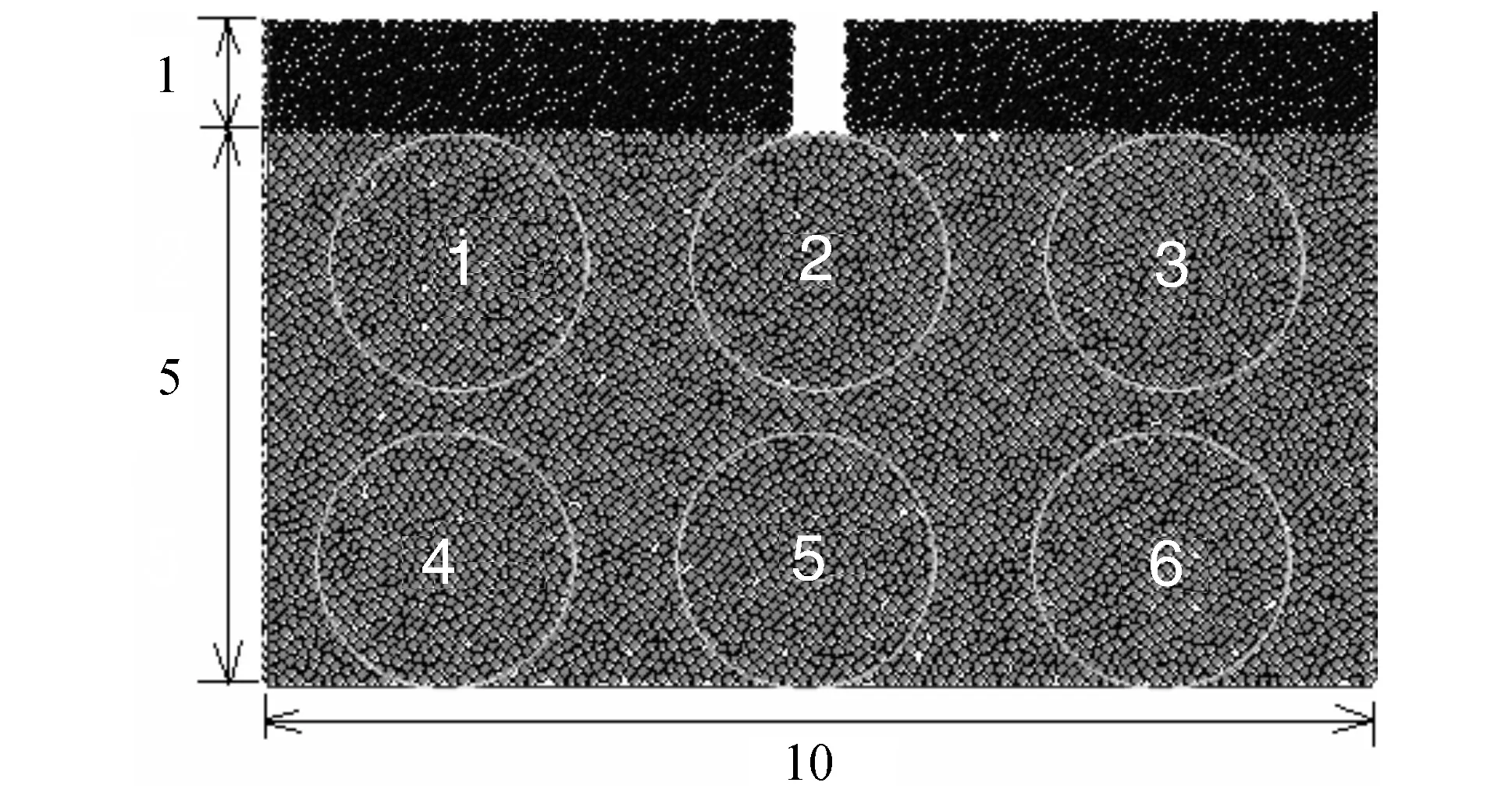
图4 测量圈的设置
3.1 孔隙率的变化
图5记录了管涌演化过程中各个测量圈内的孔隙率变化情况。
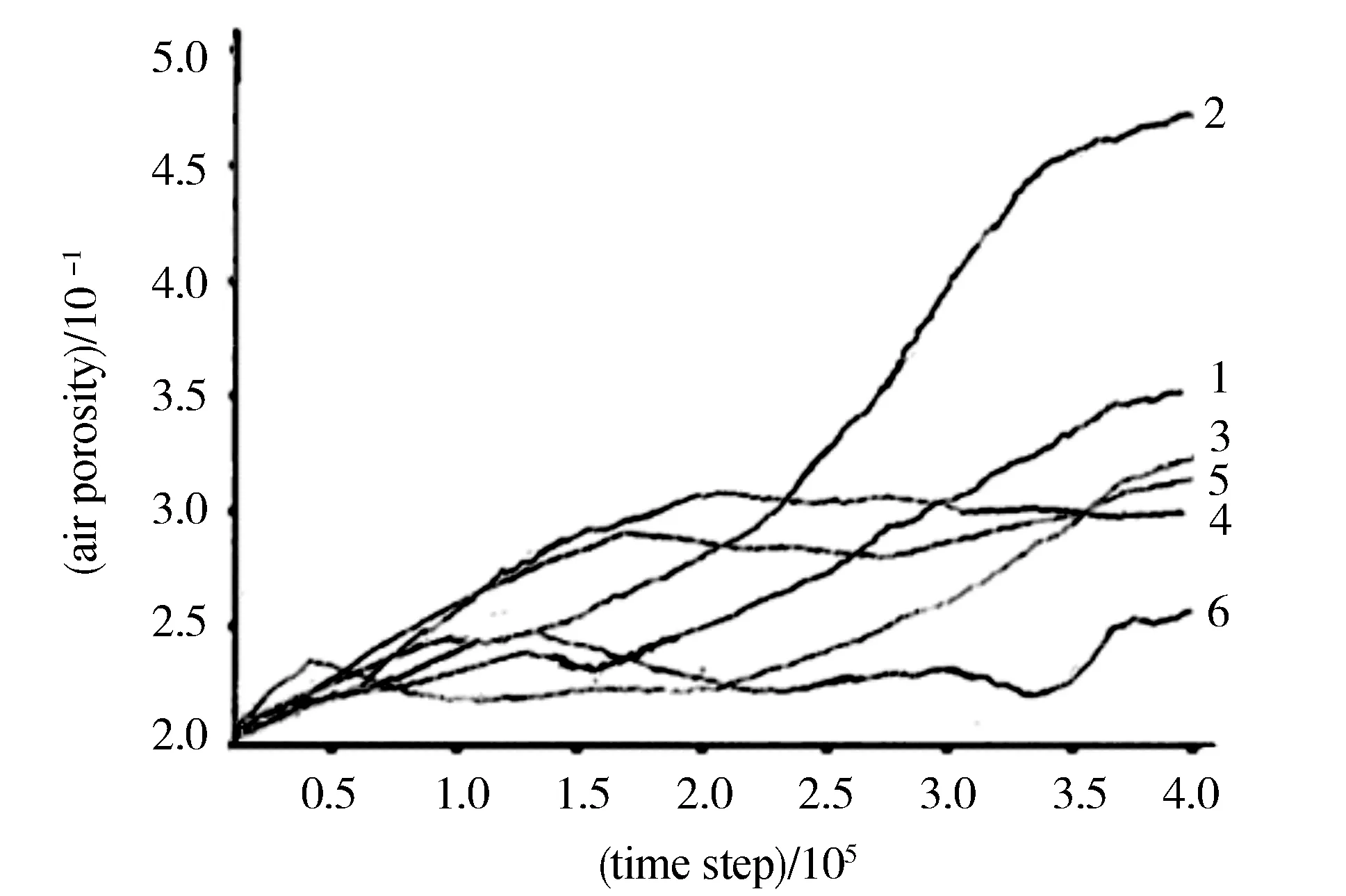
图5 各测量圈内颗粒孔隙率变化曲线图
对图5中的各条曲线进行分析可知,孔隙率总体上均呈逐渐增大的趋势,并且随着颗粒流失结束而趋于稳定,该结果与和相关研究的结论是一致的[14]。管涌口两侧靠近覆盖层的测量圈1和3的孔隙率变化基本呈加速上升的态势,这是由于在管涌发展过程中,此区域形成了渗流集中的通道,导致颗粒加速流失。曲线1比曲线3上升得更快说明左侧通道发展比右侧更为迅速,这显然是受到左侧水压力大的影响。
靠近管涌口附近的测量圈2的孔隙率变化非常明显,其对应的曲线2可划分为两个阶段:首先是稳定发展阶段,孔隙率和流速呈平缓上升;然后是迅速演化阶段,当管涌演化到一定阶段时(12万步左右),发展为加速流失阶段,曲线迅速抬升,这表明此时颗粒迅速流失。
曲线4在开始阶段逐渐上升,孔隙率由0.2增加到0.3左右,到20万步之后,又有减小的趋势。结合测量圈1的孔隙率变化曲线可以推测,曲线4的这种起伏变化是由于管涌颗粒流失后,在地层内形成了细小的通道,在测量圈1内的通道受到不断变大的水流压力的影响,最后演变成主要的渗流通道,因而孔隙率迅速增长,而测量圈4靠近通道,其孔隙率受到通道颗粒运移时压力的作用,因而孔隙率减小,密实度有所增加。
曲线5在刚开始上升较快,在15万步后,曲线呈水平状态,孔隙率保持在0.27~0.28左右,在25万步之后,曲线又出现上升。分析其原因,测量圈5位于管涌口下方,离管涌口有一定的距离,刚开始时,受到水压力的作用,颗粒虽然不能从管涌口流失,但颗粒与流体发生复杂的相互作用,颗粒结构发生了调整,变得较为松散,直到管涌口附近颗粒流失到一定程度时,此处的颗粒便开始流失。
测量圈6内的孔隙率变化过程(对应曲线6)较为复杂,有一定的起伏,曲线最后阶段才有一定的上升。这表明此位置的颗粒受到扰动,土体变疏松后又变得密实,这可能也是由于此处复杂的水—土相互作用造成的。
3.2 孔隙流速的变化
在模拟计算过程中,在各个测量圈内对流体网格内各节点上的流速进行平均,得到了管涌演化全过程中各部位的平均孔隙水流速度变化曲线,如图6所示。
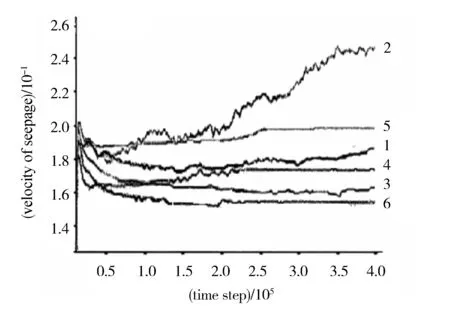
图6 各测量圈内孔隙水流速变化曲线图
通过图6中各测量圈的流速变化曲线可看出,除曲线2上升显著外,其它曲线的变化都较为平缓;曲线2在12万步左右,流速一直呈波动增长的趋势, 这正好与图5的孔隙率图反应出的颗粒流失情况相对应;曲线1、3曲线存在明显的波动,特别是曲线1在15万步之后,波动非常明显,并呈持续上升,这反应了此处流体和颗粒复杂的相互作用,从下文的图7可知,这是由于此处形成了管涌通道所造成;由于测量圈4受到测量圈1范围内的管涌通道的影响,在15~20万步时,曲线4存在较明显波动;曲线5、6基本呈一水平线,这说明管涌发生后,距离管涌口较远的位置,其孔隙流速不会发生大的变化。
结合以上对于孔隙率和流速的变化曲线的分析,可以对双层堤基管涌出口附近的演化过程进行以下的归纳阐述:管涌口下方渗透地层的颗粒在管涌发展过程中是沿着实际水流速度最大的通道溢出管涌口,管涌的发生仅会影响管涌口附近一定范围内的流速重新分布,且流速分布情况会有一个从相等的平均流速状态向局部流速集中并逐渐增大的改变过程。管涌初始阶段试样内部各处的流速相差不大,在水压力作用下,靠近管涌口的地层,其颗粒开始流失,并导致此处流速的增大,流速的增大又促进了此处管涌颗粒的加速流失,这种水与颗粒之间的相互作用始终贯穿于模拟的整个过程。管涌通道的形成,会导致通道之外的地层受到水压力的作用,局部地层有可能变得密实,但这只是暂时现象,颗粒的流失最终会导致整体地层密实度的下降。
3.3 颗粒流失的规律
图7记录了管涌口颗粒逸出到管涌地层内部通道形成的全过程。
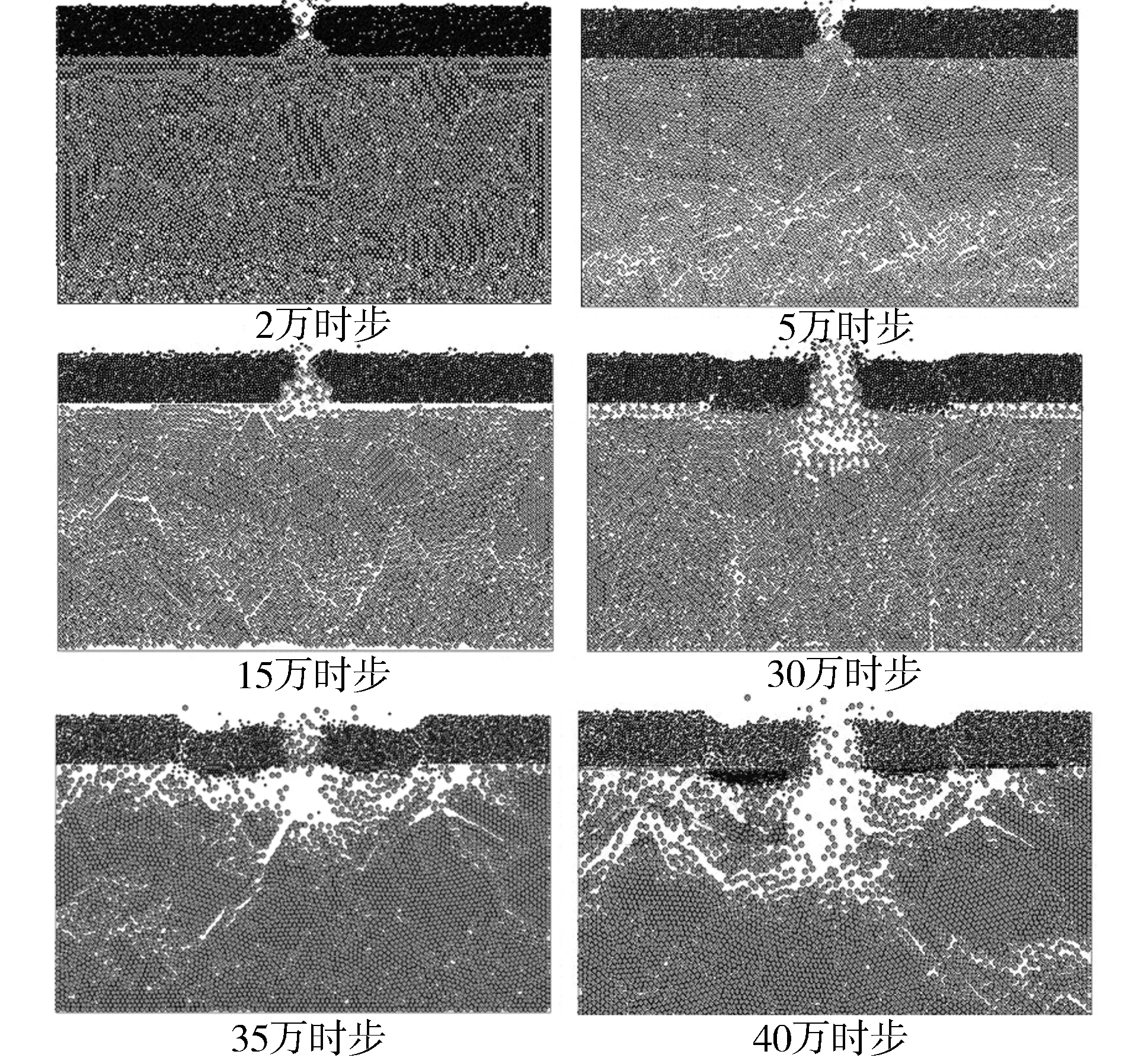
图7 管涌口PFC试样的演化
从图7可将整个模拟过程划分为管涌初期(颗粒启动,开始流失)、管涌中期(管涌口扩大,颗粒流失加快)和管涌后期(剧烈流失,形成通道)三个阶段。
0~15万时步为第一阶段。管涌口附近的砂性土颗粒由于受到水压力的作用开始流出。下卧层中,中下部颗粒的位移受到上部颗粒的限制,基本未发生移动,但由于土颗粒的不规则移动形成了一些孔隙,这些孔隙呈分散状分布在透水层的下半层。管涌继续发展,覆盖层下面靠近管涌口位置的颗粒开始流失,出现了明显的接触冲刷。
15~30万时步为第二阶段。由于下卧层管涌颗粒的流出以及水流冲刷的作用下,管涌口周围的覆盖层颗粒的粘结被破坏,管涌口边缘的黏土颗粒组强度丧失,拆散成单独的颗粒或颗粒组,并向上运动直到流失。宏观上的表现为,随着内部砂土颗粒大量涌出,管涌口开始向两侧扩展管涌开始加剧;颗粒的加速流失,导致管涌口正下方的下卧层形成了一定深度的空腔,在管涌口附近的接触层冲刷更加明显,覆盖层在重力作用下产生局部的下陷,这也解释了管涌口周围会发生地陷的原因。值得关注的是,下卧砂层内部土颗粒的不规则移动现象逐渐消失,这可能是由于水压力作用下,颗粒产生相互挤压,而当上层砂性土部分流失后,中下层颗粒之间的挤压应力释放,孔隙分布逐渐变得均匀。可以推测,在此演化阶段,颗粒的流失,并不会影响堤基的整体稳定性,堤基仍然能正常的承受上部荷载。
30~40万时步可看作第三阶段。内部颗粒从左侧(上游)大量流失,并且流失颗粒较集中的位于管涌口下部紧贴覆盖层下侧的砂性土。覆盖层下陷更加明显,管涌口继续扩大,最终透水层内部由于颗粒的流失形成较大的空腔,并向左右扩展,形成多条明显的渗流通道,并且随着通道的逐渐形成,孔隙不断增大导致流速的相对集中,周围的颗粒迅速沿通道流失。这一现象也表明,随着通道的形成,堤基的稳定性将越来越差,随着通道附近颗粒进一步被掏蚀,堤基强度将逐渐丧失,最终导致堤基破坏。
北江大堤管涌的相关资料表明:刚开始发生管涌时,管涌口水流较小,多为清水或夹杂少量细砂,流失到一定程度时,管涌口处水流会迅速增大,带出大量的泥沙[15]。本文的模拟也反映了相同的演化规律。同时,根据北江大堤石角段在94年特大洪水时的管涌测量资料得出的结论:对于多层堤基条件下透水层发生管涌前后的对比发现,透水地层的密实度有所下降,结构变得松散,砂层的有效粒径由管涌前的0.05~0.16,变为管涌后的0.15~1.1[16]。本文采用颗粒流模拟管涌时得到的细观参数的变化规律,与真实的管涌在宏观和细观上均具有一致性。
以上基于离散元原理的PFC2D程序,较好的模拟了管涌口颗粒逸出的全过程。通过模拟结果与文献[14]中的实际管涌情况对比可看出:在宏观方面,堤基管涌从发生到破坏,颗粒流出、管涌口扩展、管涌口下方透水层颗粒流失导致冲刷、管涌口周围的土层塌陷、管涌通道逐渐形成几个宏观过程得到了形象的模拟,模拟的结果与实际管涌的宏观现象基本吻合;细观方面,孔隙率和流速的变化规律也与实际情况相对应。
4 结 语
本文利用离散介质的二维颗粒流方法,通过对实际地层进行简化,建立了基于实际工程的管涌口演化颗粒流数值模型,模拟得到了水—土相互作用作用与管涌发生的全过程,分析了管涌产生与发展的细观机制。通过对管涌口附近的孔隙率、流速等细观参数的变化规律进行分析,观察颗粒流失的宏观现象,得到以下结论:
1)双层堤基管涌从发生到破坏,颗粒流出、管涌口扩展、管涌口下方透水层颗粒流失导致冲刷、管涌口周围的土层塌陷、管涌通道逐渐形成几个宏观过程得到了形象的模拟,模拟的结果与实际管涌的宏观现象基本吻合。
2)管涌口下方渗透地层的颗粒在管涌发展过程中是沿着实际水流速度最大的通道溢出管涌口。管涌口附近流速分布情况会有一个从相等的平均流速状态向局部流速集中并逐渐增大的改变,并且明显大于其他区域。距离管涌口较远的地层中,流速不会发生大的变化。渗透层的颗粒流失与孔隙流速的增加是相互影响和促进的关系,水与颗粒的相互作用始终贯穿于整个过程。颗粒的流失最终会导致整体地层密实度的下降。
3)颗粒流比传统连续介质模拟方法可以更明晰地再现土颗粒的细观参数变化轨迹,并且可以得到实际管涌过程中无法定量测的管涌发展过程中的土样特性和水流特性等数据。在得到管涌演化宏观现象的同时,可以通过分析土颗粒的运动规律,分析静力触探的细观演化规律,方便地改变应力边界条件,调节土的力学参数进行试验,因而是一种行之有效的方法。
本文仅是对管涌口的演化规律进行了较为初步计算和分析,在模拟中,涉及到参数取值及一些细部处理的问题时,模拟的结果在一定程度上缺乏说服力,但对管涌口模拟这一复杂问题而言,基于PFC2D软件,应用颗粒流理论及数值计算方法来模拟却是有益的尝试。由于目前的计算机水平限制,有些问题尚未能开展,比如对管涌过程中土体内部管涌通道的测量及演化规律等,还有待开展进一步的研究。
参考文献:
[1] 周健, 张刚.管涌现象研究的进展与展望[J].地下空间,2004,24(4): 536-542.
[2] 李守德,徐红娟,田军. 均质土坝管涌发展过程的渗流场空间性状研究[J]. 岩土力学,2005(12):2001-2004.
[3] 李守德,张晓海,刘志祥. 基坑开挖工程管涌发生过程的模拟[J]. 工程勘察,2003(2):14-17,21.
[4] 胡琦,凌道盛,陈仁朋,等. 粉砂地基深基坑工程土体渗透破坏机理及其影响研究[J]. 岩土力学,2008(11):2967-2972.
[5] 丁留谦,吴梦喜,刘昌军,等. 双层堤基管涌动态发展的有限元模拟[J]. 水利水电技术,2007(2):36-39.
[6] 周先齐,徐卫亚,钮新强,等.离散单元法研究进展及应用综述[J]. 岩土力学,2007( S1):408-416.
[7] 杨洋,唐寿高. 颗粒流的离散元法模拟及其进展[J]. 中国粉体技术,2006(5):38-43.
[8] 罗勇,龚晓南,吴瑞潜. 颗粒流模拟和流体与颗粒相互作用分析[J]. 浙江大学学报:工学版,2007(11):1932-1936.
[9] 张刚,周健,姚志雄. 堤坝管涌的室内实验与颗粒流细观模拟研究[J]. 水文地质工程地质,2007(6):83-86.
[10] Itasca Consulting Group Incorporation. PFC2D User’s Guide[R].Minneapolis, Minnesota: [s.n.], 2004.
[11] Itasca Consulting Group Incorporation.PFC2D theory and background[R].Minneapolis, Minnesota: [s.n.], 2004.
[12] 陈明东,陈国宝. 广东省北江石角堤段堤基机械管涌原因分析[J]. 工程地质学报,1998(4):28-33.
[13] 曹洪,张挺,陆培炎. 北江大堤石角段强透水堤基渗流分析[J]. 岩石力学与工程学报,2001(6):855-858.
[14] 周晓杰. 堤防的渗透变形及其发展的研究[D].北京:清华大学,2006.
[15] STERPI D. Effects of the erosion and transport of fine particles due to seepage flow[J].International Journal of Geomechanics,2003, 3(1): 111-122.
[16] 林叔忠.北江大堤石角段强透水堤基渗透变形机理初探[C]∥北江大堤石角段渗流问题技术研讨会,1998.
