高填土对隧道与道路复合结构稳定性的影响研究*

刘 镇，周翠英，黄子容，富明慧

(中山大学工学院∥岩土工程与信息技术研究中心，广东 广州 510275)

深基坑不对称高填土问题是基坑工程施工中的难题，在交通、市政、水利等工程中广泛存在，如：地铁车站、市政建筑、坝基等的基坑工程，尤其在明挖隧道及道路复合结构中越来越突出，其对隧道与道路复合结构稳定性的影响研究亟待开展。目前，在深基坑高填土稳定性计算分析中，最常用的方法是静力平衡法[1]，它主要是根据土力学理论中主动土压力和被动土压力的计算(或对计算的土压力作某些经验修正)，验算支护及明挖隧道结构抗倾覆、抗滑移等稳定性问题。其中，弹性抗力法(Snow Christopher，L.,Nickerson，Charles R 2004；殷广月，2005)针对静力平衡法中被动土压力计算中问题提出了改进[2]，用弹性地基梁法计算档墙的变位与内力，土对墙体的水平向支撑用弹性抗力系数来模拟。静力平衡法、弹性抗力法都是将桩土分开考虑，将土压力等其它外荷载单独作为作用在墙体上的荷载，将墙体作为梁考虑，不考虑墙土接触面及土的协调作用；弹性抗力有限元法虽能计算出桩身位移，但无法计算基坑周围地表及坑底变形。而有限元方法(李志高等，2003；Nejkovskij A.A., Sklyarenko,2004；Kolichko A.V.，2005)提供了一种更为合理的设计计算方法[3-7]，它可以从整体上分析填土及周围结构的应力与位移性状，而且适用于动态模拟计算，不仅为方案的设计与比较，也可为施工技术处理提供参考。无论是上述哪种方法，高填土与结构相互作用分析均是其中关键与难点。针对这一问题，本文结合深港西部通道工程，以隧道与道路复合结构为研究对象，考虑填海区复杂地质条件与道路复合结构的不对称性，利用非线性有限元法，系统的分析了高填土对隧道与道路复合结构稳定性的影响及其关键因素，提出了稳定性控制建议，从而为该类工程的设计与施工提供了依据和参考。

1 非线性有限元法简介

非线性有限元法主要包括材料非线性与几何非线性两类问题[8]。岩土体中这两种非线性均存在，但研究其如何变形主要取决于材料介质，因此，本文主要考虑岩土体的材料非线性。材料非线性平衡方程为

[K(δ)](δ)={R}

(1)

式中，[K(δ)]为劲度矩阵，{δ}为结点位移，{R} 为点荷载列阵。

根据平衡方程，结合岩土体本构关系、渗流方程等物理力学性质的定量表征与有效应力原理，就可得到岩土体非线性总控制方程：

(2)

式中：u、v、w分别为位移分量，p为孔压。

利用总控制方程，结合具体模拟计算的边界条件，就可以进行岩土体的非线性有限元求解。

2 工程简介

深港西部通道深圳侧接线工程(以下简称接线工程)，是深港西部通道的重要组成部分，接线工程是通过一线口岸深港过境车辆的专用车道，设计行车速度80 km/h，按双向六车道高速公路标准建设。接线工程主线(未含匝道)全长约4.5 km(其中地下结构长3.08 km，高架结构长0.735 km)。接线工程沿线地块可分为三类：一是大南山风景区，二是城市建设区，三是规划区。接线工程主线采用复合式道路结构(如图1所示)，地下为全暗埋下沉式道路，上覆市政道路[9-11]。

其中，接线工程自K4+073.5以东地段属于填海区[9-10]，该区分布有厚度较大、未经处理的淤泥层，该地段还断续分布有厚度变化较大的淤泥质亚粘土层，并多呈透镜体状分布，以及厚度变化较大的砾质亚粘土层。因此，该段基坑施工前已对地基中的淤泥层进行了强夯块石墩处理和爆破挤淤等处理。

该段基坑由于地质条件与施工条件的限制，北侧采用了分级大放坡开挖形式，南侧布置有由冲孔桩支撑的排洪箱。隧道北侧回填将会引起大范围的9～13 m的高填土(如图1所示)。同时，为了保持隧道结构的稳定，对箱体下部地基采用间距1.3 m直径400 mm的PHC预应力管桩处理。

图1 基坑剖面示意图

3 深基坑与高填土数值模拟

针对以上地质、结构以及基坑形式的复杂性特点，基于非线性有限元法[12-19]，通过对土体进行非线性处理、模拟土工结构、选取断面及确立边界条件，建立道路复合结构深基坑模型。

3.1 土的非线性处理

土的非线性是十分明显的，尤其接线工程位于软土分布广泛的珠江三角洲，简单的弹性或者塑性关系往往不能确切的模拟土体的应力—应变关系。为了能够较好地反映土体的非线性特征，本文采用Mohr-Coulomb强度准则与膨胀角ψf相结合的方式进行土体非线性分析。Mohr-Coulomb强度准则所提出的基本概念是岩土体材料的剪切强度由两部分[14]组成：一个是作为常量的粘聚力，一个是随法向应力变化的内摩擦角。剪切强度公式为

τf=c+σftanφ

(3)

式中：c为粘聚力，σf为破坏面上的法向应力；φ为内摩擦角。

引进的膨胀角ψf可更好的体现土体的非线性。膨胀角ψf被用来控制体积膨胀的大小，对压实的颗粒材料，当材料受剪时，颗粒将会膨胀，如果膨胀角ψf=0，则不会发生体积膨胀；如果ψf=φ，在材料中将会发生严重的体积膨胀。

3.2 土工结构的数值模拟

由于隧道结构下部的预应力管桩(PHC桩)的桩间距比较小，因此，本文采用“均质化”方法，即将桩基视为由桩和土二相组成的均质各向异性的复合材料。这样，单元剖分时不必考虑桩的存在，可减少结点未知量。同时，该方法需采用复合压缩模量Ecs来评价复合材料的压缩性，通常采用加权平均法计算，即

Ecs=mEps+(1-m)Ess

(4)

式中：Eps为桩体压缩模量，Ess为桩间土压缩模量，m为复合地基置换率。

3.3 代表性断面的选取

由于道路复合结构纵向比较长，结构纵向断面的变形约束对断面所带来的影响仅限于断面附近，对于中间段的影响可以忽略。并且横向的不均匀沉降是本文研究的主要内容，因此，可以将此问题简化为平面应变问题。

计算断面的选取综合考虑了以下几个方面因素：①在填海区内考虑下覆软弱地层(如淤泥质亚粘土)较厚，且变化较大的断面；②计算断面附近应有工程勘察钻孔点，以保持参数获取的原始性和真实性。若附近无勘察孔或者工程勘察孔较浅，下部地层信息(层位、岩土物理力学参数)无法获得，则按照就近利用勘察原则选取。按上述原则，选取里程ZXK4+127断面进行分析计算。

3.4 边界条件的确立

本文模型的基本内容包括地基土体各层土的埋深及厚度、隧道结构、PHC群桩、基坑开挖、回填土、市政道路等。为逼近实际情况，考虑远处土层对结构稳定性的影响，将模型两侧土层各向外延伸60 m左右。同时，边界条件设置如下：

1)模型中水平方向边界处的土体离结构较远，对结构的沉降影响已不明显，所以两侧外延区边界施加水平方向位移约束；

2)隧道结构左侧上部为混凝土垫层，实际中它是与南侧的排洪渠箱涵、冲孔桩联系在一起，结构稳定，难以发生水平位移，故在此处施加水平方向位移约束；

3)由于模型下部为强风化花岗岩，弹性模量较大，而且所在地层比较深，对结构的沉降影响很小，因此，计算的深度边界施加竖直方向位移约束;

4)地表为自由面。由于该道路复合结构位于填海区，所以必须考虑孔隙水压力与土体变形之间的关系。土体的为多孔介质，不施加任何边界条件的边界假定为不排水边界，地表是排水条件，即排水边界为自由表面。

3.5 计算参数的选取

道路复合结构稳定性计算参数选取主要涉及到下卧层、回填土、强夯复合地基三方面。

针对下卧层力学参数，基于接线工程的填海区地质勘察资料，结合该地区地质工程经验，对勘察所得岩土力学参数进行修正，其结果见表1。

针对回填土力学参数，根据接线工程设计方案，路基设计填料为砂质粘性土或砾质粘性土分层回填筑实，结合《公路路基设计规范》(JTGD30-2004)，选择合理的岩土力学参数作为回填土计算参数，见表1。

针对强夯复合地基力学参数，根据《复合地基设计和施工指南》(龚晓南，2003)，将此复合地基中增强体与基体两部分视为一复合土体，采用复合压缩模量来评价此复合土体的压缩性，同时考虑地基处理的达标要求，得到：块石墩复合地基变形模量大于18 Mpa，置换区变形模量为19 Mpa，见表1。

此外，市政道路均布荷载为车道荷载，其数值根据《公路桥涵设计通用规范》(JTG D60-2004)中车道荷载标准值换算得到，为2.8 KN/m。

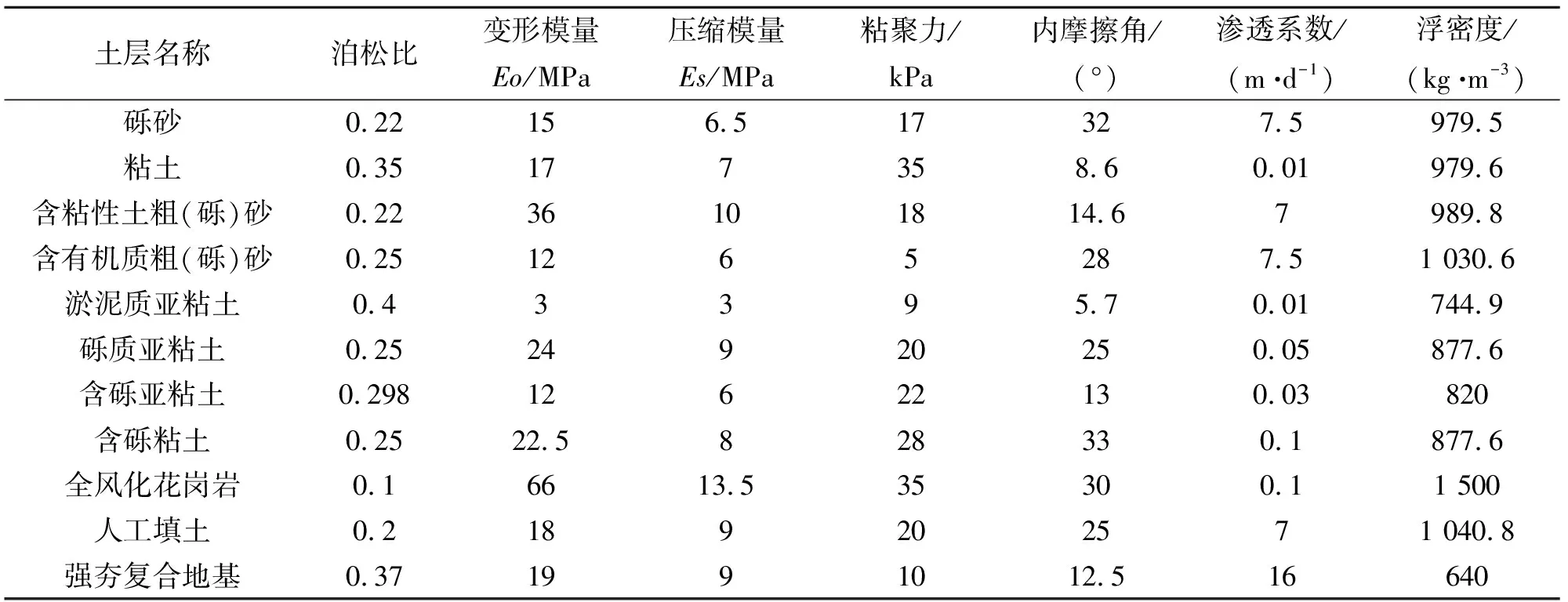
表1 岩土力学参数表

综合上述模型、边界、参数，建立如图2所示的道路复合结构稳定性有限元计算模型，并采用映射单元法进行网格划分。

图2 高填土条件下隧道与道路复合结构的稳定性分析模型

同时，为了叙述方便，按图3所示对隧道与道路复合结构的各个控制点进行编号，隧道结构用1、2、3、4点来标记，市政道路用A、B、C、D点来标记。

图3 隧道与道路复合结构各控制点的编号

4 高填土稳定性影响分析

4.1 计算结果与分析

根据上述建立的稳定性分析模型，运用ADINA软件，对接线工程ZXK4+127断面进行模拟计算，得到：隧道与道路复合结构各控制点的位移(见表2)，以及整个计算区域的有效应力(如图4所示)与位移(如图5-图7所示)。

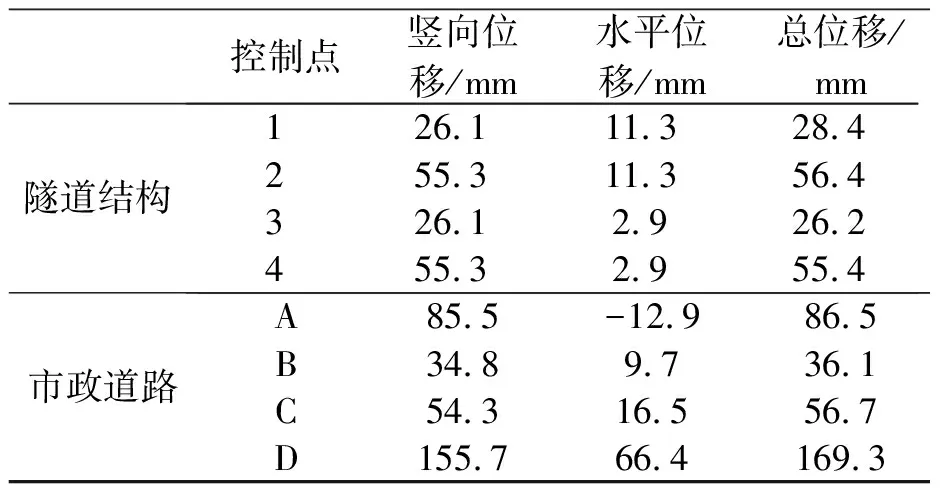
表2 隧道与道路复合结构各控制点的位移1)

1)竖向位移以向下为正；水平位移以北为正

图4 有效应力云图

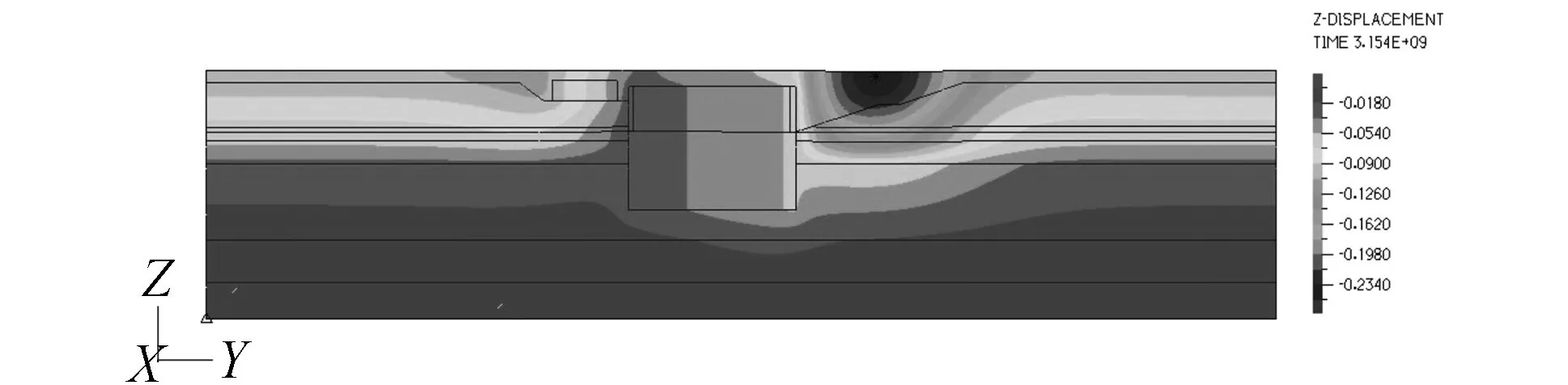
图5 竖向位移云图

图6 水平位移云图

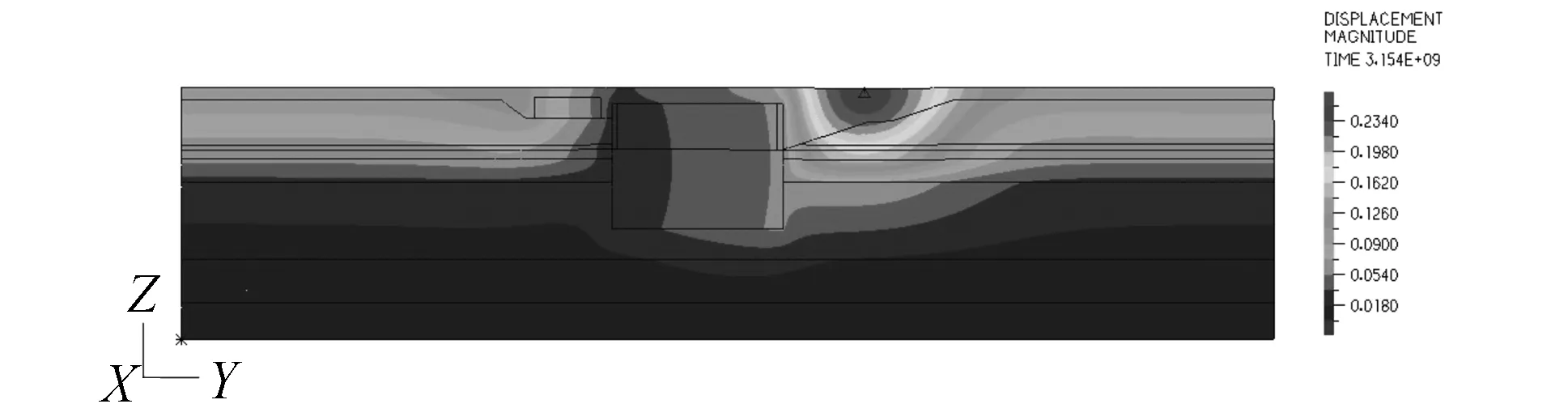
图7 总位移云图

根据上述计算结果，下面从有效应力与位移两方面来分析高填土对隧道与道路复合结构稳定性的影响。

4.1.1 有效应力 由图4可知，较大应力主要发生在道路复合结构的北侧和顶部，在隧道结构北上方的角点处达到最大，说明这些位置存在应力集中现象，易造成该侧隧道结构变形与开裂。

4.1.2 位移 高填土对隧道与道路复合结构位移的影响主要包括竖向位移与水平位移两方面。

对于竖向位移，由表2可知，隧道结构两侧控制点1与2(或控制点3与4)的差异沉降为29.2 mm；南侧市政道路两端控制点A与B的差异沉降为50.7 mm；北侧市政道路两端C点与D点的差异沉降则达到了100.4 mm。由此可得：上覆于北侧高填土的道路控制点差异沉降也明显大于南侧；而北侧高填土处隧道结构控制点差异沉降未明显大于南侧；易引起道路复合结构整体失稳。结合图5还可得到：①最大竖向位移出现在隧道北侧大放坡中部位置，且在高填土中部的地表处达到最大，为230 mm，由此处向两侧逐渐减小，形成一个凹部，北侧道路伸出隧道结构外的部分正好位于凹部的左侧，其竖向位移为156 mm；②隧道南北两侧与土体交界的部位竖向位移沿水平向的变化梯度较大，即隧道上方土体和隧道外侧土体的差异沉降很大，易在此处出现纵向裂缝，骑跨隧道的北侧市政道路很可能在此位置开裂。

对于水平位移，由图6可知，道路复合结构上部及其周围土体的水平位移总体上是向北的，而下部的PHC群桩区和下卧层的水平位移总体上是向南的，隧道结构按顺时针方向发生了微小转动，约为0.05°。说明：高填土对市政道路稳定性的影响要大于对下埋隧道结构的影响。同时，最大南北向水平位移都发生在紧邻隧道结构北侧、填土厚度最大的位置，填土顶部发生最大的北向位移，隧道结构北侧角点填土发生最大的南向位移。这说明道路复合结构北侧填土体在竖向上的水平位移变化梯度较大，易造成该侧隧道结构变形与开裂。

此外，由图5和图7对比可知，总位移云图和竖向位移云图非常相似，最大总位移也发生在高填土中间顶部位置，这说明道路复合结构的竖向位移是主要的，而水平向位移所占比重较小。

4.2 高填土影响的关键因素与稳定性控制建议

根据上述高填土对隧道与道路复合结构的影响的分析可知，最大的有效应力、位移均集中北侧高填土区域，究其原因在于：

1)高填土本身的压缩变形对箱体将产生较大的负摩擦力，加之下卧软弱土层厚度分布不均匀，造成了该处道路复合结构差异沉降及竖向位移、总位移较大；

2)9～13 m高填土本身巨大的水平向压力，造成了该处道路复合结构水平位移较大，并产生转动。

3)单侧高填土的不对称性及其形状特殊性(楔形)，造成了该处出现应力集中现象。

上述3点原因从根本上说，均是高填土自重引起的变形毫无分担的直接作用于道路复合结构的结果。因此，高填土自重是道路复合结构稳定性控制的关键因素。为此，本文认为应从以下3个方面对控制高填土条件下道路复合结构的稳定性：

1)从高填土自重分担角度，建议采用合适结构(如：高承台)承担高填土的部分自重，并将其传递至基岩，减少其自身变形及对道路复合结构的影响；

2)从高填土直接作用角度，建议采用合适结构(如：隔离墙)阻隔高填土对隧道结构的直接作用，减少其变形直接对道路复合结构的影响；

3)从单侧高填土不对称性角度，建议采用合适结构(如：加筋土)铺设在骑跨隧道的市政道路下方，减少其下沉造成的差异沉降影响。

5 结 论

1)依托深港西部通道工程，考虑填海区复杂地质条件与道路复合结构的不对称性，采用非线性有限元法进行隧道与道路复合结构稳定性模拟计算，分析了高填土对其位移、应力的影响，表明：高填土对市政道路稳定性的影响要大于对下埋隧道结构的影响。

2)通过分析高填土对道路复合结构稳定性影响的原因，提出了其影响控制因素，并从高填土自重分担、直接作用与不对称性三个角度，提出了道路复合结构稳定性控制建议，为该类工程的设计与施工提供了依据和参考。

参考文献：

[1] 罗火生，洪宝宁.高速公路软基处理中高填土路堤的稳定性控制[J]. 交通科技，2003(3)：37-39.

[2] 殷广月.高填方路堤常见病害及治理[J].辽宁交通科技，2005(5):52-53.

[3] SNOW C, NICKERSON L ,CHARLES R. Case study of EPS Geofoam lightweight fill for settlement control at bridge approach embankment[J]. Geotechnical Special Publication,2004,1261:580-589.

[4] 李志高，刘国明，欧志东.高填路基稳定问题的非线性有限元分析[J].福州大学学报:自然科学版，2003，31(1):73-77.

[5] NEJKOVSKIJ A A,SKLYARENKO A V.Experience of designing and construction of the Chirkey HPP foundation pit (FP)[J]. Gidrotekhnicheskoe Stroitel'stvo, 2004(9):39-42.

[6] KOLICHKO A V. Studying the features of formation of the stable slopes (SS) for foundation pits (FP) and underground workings (UW)[J].Gidrotekhnicheskoe Stroitel'stvo, 2005(3): 32-34.

[7] 李小青，张欣.高填方路堤沉降的数值分析研究[J].土工基础，2005，19(3)：56-58.

[8] 谢康和，周健.岩土工程有限元分析理论与应用[J].北京：科学出版社，2002.

[9] 上海市政设计研究院，深圳市勘察研究院.深港西部通道深圳侧接线工程工程地质勘察报告[R].2003.

[10] 深圳市岩土综合勘察设计有限公司.深港西部通道深圳侧接线基坑支护工程Ⅰ标段设计施工图[R].2006.

[11] 上海市政工程设计研究院，重庆交通科研研究设计院，合乐中国有限公司.深港西部通道深圳侧接线施工图集-地道结构[R].2005.

[12] 张冰峰，秦四清.某地基不均匀沉降的三维分析[J].工程地质学报，2002，10(2)：184-187.

[13] 杜守继，朱建栋.穿越铁路的地道结构与土相互作用的数值模拟[J].地下空间与工程学报，2005，1(2)：242-246.

[14] 赵坚，李海波.莫尔-库仑和霍克-布朗强度准则用于评估脆性岩石动态强度的适用性[J].岩石力学与工程学报，2003，22(2)：171-176.

[15] 李小青，张欣.高填方路堤沉降的数值分析研究[J].土工基础，2005，19(3)：56-58.

[16] 邢仲星，陈晓平.复合地基力学特性研究及有限元分析[J].土工基础，2000，14(2):1-4.

[17] 王春生，周翠英.梅河高速公路隧道稳定性数值模拟[J].中山大学学报：自然科学版，2005，44(1)：38-40.

[18] 刘祚秋，富明慧，周翠英.变荷载下任意层地基一维非线性固结的数值分析[J].中山大学学报：自然科学版，2007，46(5)：1-4.

[19] 刘祚秋,周翠英.软粘土地基非线性一维大变形固结的有限差分法分析[J].中山大学学报：自然科学版，2005，44(3)：25-28.