协作CDMA系统上行链路功率控制策略及优化算法研究*
2010-06-05黄高飞张广驰秦家银
黄高飞,张 萍,张广驰,唐 冬,秦家银
(1.中山大学电子与通信工程系,广东 广州 510275;2.广州大学电子信息工程系,广东 广州 510006)
近年来,协作通信技术的理论和应用研究倍受学界和业界的重视[1-2]。但目前的有关研究大都基于各种理想假设条件,没有与具体的实际系统相联系,很少考虑技术的可实现问题,要真正把协作通信的理论成果应用于实际通信系统,还有诸多的问题有待解决。为了把协作通信技术应用于无线CDMA系统,Sendonaris等[3-4]提出了协作CDMA系统的实现方案,但其研究都假设CDMA码字严格正交,而协作CDMA系统是异步传输,其码字的正交性被破坏,特别是其上行链路,更应该考虑码字的非正交性问题。在无线CDMA系统的上行链路中,考虑码字不正交时,接收机接收来自各个无线终端的信号时就会存在用户间干扰,Cao Yang[5]、Venturino[6]、Huang Wan-Jen[7]、Yang Hao-Jie[8]等提出了协作CDMA上行链路的多用户检测方法,以最大程度地抑制用户间干扰。然而,他们的研究都是假设各个源节点和中继节点以恒定功率发送,没有采用功率控制,因此,该方案在节省终端功率、降低到达接收机的用户间干扰功率以及增加系统容量等方面都存在明显的缺陷。为了减小系统多点接入干扰,Wang Bin[9]、Pham Tung T[10]等提出了协作CDMA系统上行链路中基于几何规划求解的功率控制算法,其优化目标是每个用户在基站接收的SINR (Signal to Interference plus Noise Ratio) 满足最小下限的条件下,最小化系统总功率,该优化方法可以得到系统功率向量的最优解,但是其算法复杂度太高,而且基于集中式控制,需获得基站、各个中继和源端之间的信道信息,可实现性差。
在文献[9]的基础上,针对采用DF (Decode and Forward) 方式的协作CDMA系统上行链路,根据最优化问题的分解理论和协作通信系统分阶段传输数据的特点,我们提出了分段式的低复杂度功率控制策略及其算法:第一阶段源结点发送数据时,采用传统CDMA无线网络中的分布式功率控制方法,该方法不需获得信道信息,其收敛速度快、复杂度低;第二阶段中继结点发送数据时,则采用基于几何规划求解的功率控制方法,该方法虽然是集中式的功率控制,但在基站只需获得从各个中继结点至基站的信道信息,而且采用几何规划求解的计算量比文献[9]小得多。理论分析和数值仿真表明,相对于文[9]算法,本文提出的新算法运算量小、复杂度低、收敛速度快,且收敛于全局最优。
1 系统模型
考虑一个存在N个源结点S1、S2、……、SN和N个中继结点R1、R2、……、RN的CDMA蜂窝系统上行链路,源结点Si通过中继结点Ri与基站Bs进行通信,如图1所示。

图1 系统模型
在此系统模型中,假设以下条件成立:
1) 每个源结点存在且仅存在一个中继结点协作转发;
2)中继结点采用DF的协作转发方式,工作于半双工模式;
3) 各个源结点产生恒定数据速率R的单一业务数据帧,每个数据帧的长度相同,接收机正确解码数据帧的最小SINR阀值为;
4) 从各个结点至基站的数据传输过程分为时间相等的奇数和偶数时隙两个阶段,每个阶段发送一个数据帧:在奇数时隙的第一阶段源结点发送数据,中继结点和基站接收数据;在偶数时隙的第二阶段中继结点转发收到的数据,基站接收来自中继结点的数据,源结点处于等待的“静止”状态。
设Si和Ri的发射功率功率分别为Psi、Pri,从源结点Si至基站的信道增益为Gsib,从中继结点Ri至基站的信道增益为Grib,从源结点SMi至中继结点Rj的信道增益为Gsirj。
第一个阶段基站接收第i个源结点的SINR为
(1)

而第一个阶段第i个中继接收第i个源结点信号的SINR为
(2)
为保证中继结点对数据帧成功译码,须有γsr,i≥γth。
在第二个阶段,基站接收第i个中继结点的SINR为
(3)
在此假设基站采用最大比合并MRC (Maximum Ratio Combining) 方式合并两个阶段接收到信号,为译码第i个源结点发送的数据帧的接收SINR为
γi=γs,i+γr,i
(4)
为保证基站能对数据帧成功译码,须有γi≥γth。
2 协作CDMA系统上行链路功率控制策略及优化算法
在传统的CDMA无线网络中,功率控制算法的基本原则是在满足系统各个用户SINR要求的条件下最小化系统总功率。我们按照这一原则,提出一种DF方式下协作CDMA系统上行链路的低复杂度功率控制策略及优化算法。
根据系统模型的分析,可以把DF方式下协作CDMA系统上行链路的功率控制问题描述为:

(5)
s.t.γsr,i≥γthi=1,2,…,N
(6)
γi=γs,i+γr,i≥γthi=1,2,…,N
(7)
Ps,i,Pr,i≤Pmaxi=1,2,…,N
(8)
其中γs,i、γsr,i和γr,i分别在(1)-(3)式中给出。
2.1 基于几何规划的功率控制优化算法
为了得到最优功率解向量P=[Ps1,Ps2,…,PsN,Pr1,Pr2,…,PrN],文献[9]提出了基于几何规划的最优化求解算法,其求解的基本思路是把不等式(6)、(7)左边的表达式化为正项表达式,即具备以下形式:

(9)
然后利用几何规划问题的求解方法进行求解。但是,由于(7)式不能直接化为符合(9)式的正项表达式形式,所以问题1不是标准的几何规划问题,无法直接利用几何规划问题的求解方法得到全局最优解。在文献[9]中,通过利用文献[11]的结论把(7)式近似为正项表达式的形式,并进行多次标准几何规划问题的迭代求解,最终使功率向量P收敛到全局最优解。由于需进行多次标准几何规划问题的迭代求解才能得到全局最优解,而进行一次标准几何规划问题求解也需多次迭代运算才能完成,因此利用此优化算法进行一次功率控制的总迭代运算次数比较多,收敛速度比较慢。此外,此功率控制优化算法是基于集中式的,必须获得基站、各个中继和源端之间的信道信息。所以,此功率控制算法具有很高的复杂度,可实现性差。
2.2 低复杂度的功率控制策略及优化算法
根据协作通信系统分为两个阶段进行数据传输的特点,我们把DF方式下协作CDMA系统上行链路的功率控制分为两个阶段进行。在第一个阶段源结点发送数据时,分别由各个中继结点对其协作的源结点进行功率控制;而在第二个阶段中继结点转发数据时,由基站对中继结点进行功率控制。在此,为简化分析,假设中继结点的选择为最优,使两个阶段中功率控制的系统功率向量最优解总是存在。下面证明此分阶段功率控制策略可以得到问题1的全局最优解:
证明:根据文献[12]中的最优化问题分解理论,采用原始分解(primal decomposition)方法可把问题1分解为以下两个子问题:

(10)
s.t.γr,i≥γr,i=γth-γs,ii=1,2,…,N
(11)
Pri≥Pmaxi=1,2,…,N
(12)

(13)
s.t.γsr,i≥γthi=1,2,…,N
(14)
Psi≥Pmaxi=1,2,…,N
(15)
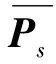
根据以上分析,在DF方式下协作CDMA系统上行链路,第一个阶段源结点发送数据时,分别由各个中继结点对其协作的源结点进行功率控制,可以由问题3描述;而在第二个阶段中继结点转发数据时,由基站对中继结点进行功率控制,可以由问题2描述。证毕。
在第一个阶段功率控制对应的问题3中,其求解可借助文献[13]提出的Ad hoc无线网络功率控制算法进行。文献[11]证明了单跳功率控制可以借助于传统无线CDMA网络中的分布式功率控制迭代算法,以最小化Ad hoc网络单跳数据传输的系统功率,即
(16)
其中Pi(t)为t时刻第i个结点的发射功率,γtgt为目标SINR,γi为t时刻中继结点接收第i个源结点发送数据的SINR。在采用协作通信的蜂窝系统上行链路中,从源结点至中继结点的数据传输过程与Ad Hoc网络的单跳数据传输过程是相同的。因此,可以使用分布式迭代算法得到问题3的最优解
(17)
其中Psi(t)为t时刻第i个源结点的发射功率,γsr,i为t时刻第i个中继结点接收第i个源结点发送数据的SINR。
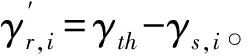
结合式(3),问题2中的(11)式可化为:
(18)
显然,上式不等号左边的表达式是与(9)式形式相同的正项表达式。因此,问题2是标准的几何规划问题,直接进行一次几何规划求解即可得到其全局最优解。
综合上述对问题2和问题3的求解过程,由于在第一个阶段引入了传统无线CDMA网络的分布式功率控制算法,以及第二个阶段的功率控制过程只需进行一次标准几何规划问题求解,因此基站只需获得各个中继结点至基站的信道信息,而且所需要的迭代运算比文献[9]提出的功率控制算法的运算量小很多。
3 仿真结果

首先,我们比较了文献[9]中基于几何规划的功率控制方法与本文所提出的功率控制方法在不同终端结点功率约束下得到的系统总功率最优解。

表1 仿真参数设置
图2和图3是系统存在7个源结点、γth分别为3 dB和5 dB时得到的结果。从图中可以看出,两种功率控制方法所得到的解是完全相同的,即两者都可以收敛到问题1的全局最优解。

图2 γth=3 dB时不同终端功率约束下的最优解

图3 γth=5 dB时不同终端功率约束下的最优解
表2比较了文[9]中功率控制优化算法与本文所提出的功率控制优化算法的运算复杂度。表2列出了系统源结点数量N不同时两种功率控制优化算法收敛到全局最优解所需平均迭代次数。
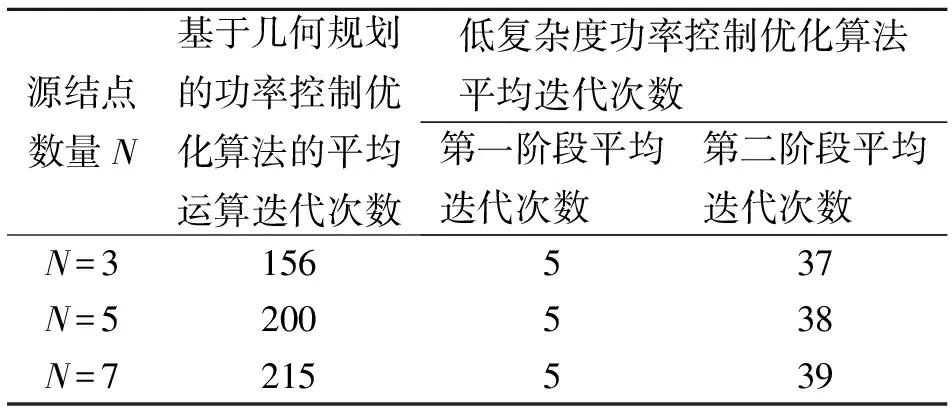
表2 系统源结点数量不同时两种功率控制优化算法的运算复杂度
对不同的N,分别在各个结点与基站的距离不同条件下进行1 000次实验。实验中假设γth=5 dB,而各个终端结点最大功率约束为Pmax=0.1 W。
从表2中可以看出,我们提出的功率控制优化算法平均迭代次数比文献[9]的功率控制优化算法要少很多。而且,由于求解问题2的迭代运算只需按(17)式进行,其运算量比以几何规划求解问题1的一次迭代运算量小很多。此外,问题3的求解变量比问题1的求解变量少,以几何规划求解问题3的一次迭代运算量比求解问题1的一次迭代运算量也小。因此,本文提出的功率控制优化算法比文献[9]的功率控制优化算法具有更低的复杂度和更快的收敛速度。
4 结 论
在采用DF方式的协作CDMA系统上行链路中,为了减小多用户接入干扰和节约终端功率,本文提出了一种低复杂度的功率控制策略及优化算法。理论分析和数值仿真结果表明,与文献[9]相比,该功率控制优化算法需要的信道信息更少,运算迭代次数和运算量大大减少,具有更低的复杂度和更快的收敛速度,且收敛于全局最优。
参考文献:
[1] LANEMAN J N. Cooperative diversity in wireless networks: algorithms and architectures[D]. Massachusetts Institute of Technology, 2002.
[2] 李军怀,高苗,张璟.基于能耗的协同感知消息传递方法[J]. 中山大学学报:自然科学版, 2009, 48(1):113-117.
[3] SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity—part I: system description[J]. IEEE Transactions on Communications, 2003, 51(11): 1927-1938.
[4] SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity—Part II: implementation aspects and performance analysis[J]. IEEE Transactions on Communications, 2003, 51(11): 1939-1948.
[5] CAO Y, VOJCIC B. MMSE multiuser detection for cooperative diversity CDMA systems[C]∥IEEE Wireless Communications and Networking Conference (WCNC), Atlanta USA,2004: 42- 47.
[6] VENTURINO L, WANG X D,LOPS M. Multiuser detection for cooperative networks and performance analysis[J]. IEEE transactions on signal processing, 2006, 54(9): 3315-3329.
[7] HUANG W J, HONG Y W, KUO C C. Relay-assisted decorrelating multiuser detector (RAD-MUD) for cooperative CDMA networks[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(3): 550-560.
[8] YANG H J,HUANG W J, WANG Y S. Reduced-rank multiuser relaying (RR-MUR) scheme for uplink CDMA networks[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei China, 2009: 102-108.
[9] WANG B, ZHAO D M. Optimum power distribution for uplink channel in a cooperative wireless CDMA network[C]∥IEEE International Conference on Communications (ICC), Beijing China, 2008: 4795-4801.
[10] PHAM T T, NGUYEN H H. A simple decorrelate-and-forward relaying scheme for multiuser wireless CDMA networks[C]∥International Conference On Communications And Mobile Computing, Leipzig, Germany, 2009: 232-236.
[11] CHIANG M, TAN C W, PALOMAR D P. Power control by geometric programming[J]. IEEE Transaction on Wireless Communications, 2007, 6(7): 2640-2651.
[12] PALOMAR D P, CHIANG M. A tutorial on decomposition methods for network utility maximization[J]. IEEE Journal on Selected Areas in Communications, 2006, 8(24): 1439-1451.
[13] ELBATT T, EPHREMIDES A. Joint scheduling and power control for wireless ad hoc networks[J]. IEEE Transaction on Wireless Communications, 2004, 3(1): 74-85.
