电机铁耗的有限元计算方法研究进展及有待解决的问题*

刘晓芳， 赵海森， 陈伟华， 顾德军

(1.华北电力大学电气与电子工程学院，北京 102206;2.上海电科电机科技有限公司，上海 200063)

0 引言

随着超高效电机研制工作的深入开展［1］，传统基于磁路分析的电磁计算方法［2-3］越来越难以满足对深入研究电机铁耗的要求，这主要是因为该方法在计算铁耗时通过引入经验系数计及铁耗的众多影响因素，并不能针对某一特定因素对铁耗的具体影响程度进行分析;此外，该方法只针对齿部和轭部两段磁路进行计算，且计算结果仅反映总铁耗，并不能对铁心局部损耗分布进行细致分析，很难为开展结构优化等降耗措施研究提供技术支持。基于有限元法的铁耗计算方法具有计及因素全面、计算精度高等优点，已成为国内、外同行的一个研究热点。

原则上讲，铁耗有限元计算和研究可分为2-D和3-D两类算法。虽然也有文献研究了利用3-D有限元法进行铁耗计算，如文献［4］，但其计算时间太长且占用资源过多。例如，作者利用一台内存为4 GB、CPU为Intel Q9550的计算机，对定子外径为90 mm的低速永磁电机进行3-D稳态有限元计算，共剖分43万个四面体单元，计算一个点需要15 min，如果进行时步计算，假设计算2 000个点，耗时长达数百小时，故从应用角度考虑，当前阶段2-D有限元仍是最佳选择。

目前，利用有限元法计算铁耗的基本计算模型主要有两种:一是基于磁滞和涡流损耗的两项式模型［2-3］;另一个是由Bertotti于1988年在文献［5］中提出基于磁滞、涡流及附加损耗(Excess loss)的常系数三项式模型，该模型已得到广泛应用［6-8］，在上述基本计算模型基础上，还衍生出其他一些改进模型［9-14］。此外，以上模型均通过硅对钢片实测损耗拟合求得，目前在国际范围内得到普遍认可的测试方法为爱普斯坦方圈和环形样品测试［15-17］，故这些模型均通过对这两种测试方法测得的损耗数据拟合得出，对此文中将逐一介绍。

本文主要目的有以下两点:一是介绍基于2-D有限元法的交流电机铁耗计算方法研究进展，其中重点介绍了铁耗计算基本模型、部分改进模型及模型中损耗系数求解方法，并列举相应算例;二是结合工程实际需求，指出了铁耗有限元计算方法有待解决的问题。

1 电机铁耗有限元法计算方法

1.1 交流电机铁耗与铁磁材料损耗的区别

由文献［2-3］可知电机铁耗和铁磁材料损耗的产生机理不同，其主要差别在于旋转磁化，在交变磁化下，磁密矢量仅大小变化，其轨迹为一条直线，而在旋转磁化作用下的磁密矢量除大小变化外，方向也发生变化，其轨迹呈椭圆形，两者对比如图1所示。这两种磁化方式产生的损耗不尽相同，文献［3］中指出电机轭部磁通密度一般为1.0～1.5 T，相应旋转磁化产生的磁滞损耗要比由交变磁化产生的磁滞损耗约大45%～65%，因此在计算电机铁耗时，必须考虑旋转磁化的影响。至于如何计及，传统的铁耗工程计算方法是靠引入经验系数实现［2-3］的;而利用有限元法计算铁耗时，仅需对计算得到的磁密进行相应处理即可。

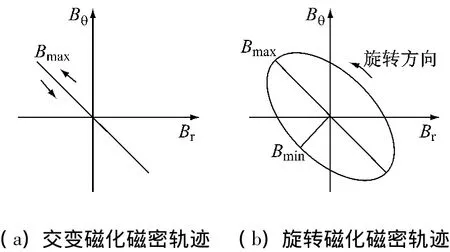
图1 交变磁化和旋转磁化示意图

1.2 2-D有限元法可计及的电机铁耗影响因素

除了磁化方式这一根本区别外，交流电机铁耗与铁磁材料损耗的区别还包括磁密分布不均匀、制造工艺及谐波磁场等。因此，对2-D有限元法能够计及的铁耗影响因素分析如下:

(1)磁密不均匀分布。通过有限元计算能够得到铁心内部任意区域的磁密分布情况。

(2)谐波磁场。利用有限元法计算得到的磁密随时间变化波形中已包含基波和谐波磁场。

(3)旋转磁化。通过对计算得到的磁密进行相应处理便可计及。

(4)机械加工因素。对于未经退火的冷轧硅钢片，冲剪应力也是影响铁耗的一个重要因素;此外，压装也会导致铁心受力发生变化，影响其导磁性能。这些因素可通过对模型进行处理计及。

尽管利用2-D有限元法能够较全面计及上述几种主要因素，但由于其自身局限性，仍有个别因素难以计及，例如端部漏磁场在附近金属构件中产生的损耗、加工中产生的毛刺，以及压装时导致硅钢片的片间绝缘破坏产生的损耗等。考虑到利用有限元法计算铁耗的主要目的在于针对上述能够计及的某一特定因素，系统研究其对铁耗的影响程度，在此基础上进一步研究降耗措施，这一点是传统电磁计算无法实现的;此外，端部磁场产生的损耗在总铁耗中仅占很小一部分［3］，而对于毛刺和片间绝缘这两种因素，随着制造工艺水平的日益提高，其对铁耗的影响也会降低且可通过试验方法展开研究，故这些难以计及的因素并不会妨碍有限元法在铁耗计算与分析中的应用。此外，需说明的是，本文重点在于介绍铁耗计算基本模型，对于如何计及旋转磁化和机械加工因素，属于另一个研究方向，文中对此不做分析。

1.3 利用有限元法计算电机铁耗的特点

有限元法可以方便得到电机内部磁场分布，因此在计算铁耗时对结果处理更具灵活性，其特点主要体现在以下几方面:

(1)通过计算能方便地得出电机铁心内部各区域磁密随时间变化的波形。

(2)在铁耗计算时可灵活选择磁密波形的处理方法，既可以直接利用计算得到的磁密波形计算铁耗，也可以利用傅里叶分解得到基波和谐波磁密后，再分别计算相应铁耗。

(3)可任意选择不同区域(磁路)进行计算，例如齿肩、齿根及扣片槽附近等多个局部区域。

(4)空载和负载条件下由基波和谐波磁场产生的损耗均可单独计算。

2 基于有限元法的铁耗基本计算模型

2.1 常系数三项式模型

2.1.1 模型介绍

该模型由Bertotti于1988年提出，由磁滞、涡流及附加损耗组成的三项式模型，可表示如下［5］:

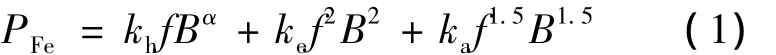
式中，kh、ke和ka均为损耗系数。式中第一项是磁滞损耗;第二项对应于经典涡流损耗。其中ke=π2γd2/6ρ，d为硅钢片厚度，单位 m;γ 为电导率，单位S/m;ρ为铁磁材料密度，单位kg/m3。第三项是由于磁畴壁不连续运动产生的巴克豪森跃变产生的损耗，文献［5］中称之为附加损耗。

常系数三项式模型如式(2)所示，但其仅适用于磁密波形为正弦时的铁耗计算。众所周知，即使在正弦电源供电条件下，磁密波形仍含有谐波，因此需要一种能够适用于任意波形的铁耗计算模型，关于这一问题的解决方法，早在20世纪70～80年代，J.D.Laver通过试验研究，在对大量试验数据进行分析的基础上，提出涡流和磁滞损耗的修正方法［18-19］，将其与式(2)结合后可得目前常用的任意磁密波形下铁耗计算公式［6-8］:

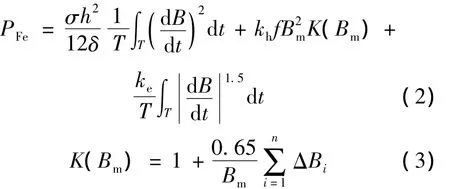
式中:σ——铁磁材料电导率;

h——铁心叠片厚度;

δ——铁磁材料密度;

T、f——基波的周期和频率;

Bm、ΔBi——一个周期内磁密最大值和局部磁密变化量;

n——局部磁密变化次数［6-8］。

上述模型是目前利用有限元计算电机铁耗最常用的一种模型，在其精度方面，Bertotti在文献［5］中指出该模型对于大多数硅钢片的计算误差在10%以内，足以用其描述电机内部损耗特性。

2.1.2 模型中损耗系数求解

为了方便其他系数的求解，首先说明Steinmetz系数α的取值，由传统电机设计理论可知，其值一般取1.6～2.2［2-3］，但在该模型中，参考其他文献研究结果，取其值为2。这样取值的原因如文献［20］所述:电机内部磁密通常在1.2～1.5 T附近，只有个别地方磁密可高于1.5 T，而在低于1.5 T时，取a=2的计算结果精度仍可很好地满足工程需求。实际上，该系数仍可通过对实测损耗数据进行拟合求得，该方法将在后续内容的变系数三项式模型中介绍。对式(2)所示常系数模型可作如下处理:

以下基于式(4)说明上述系数的具体求解方法。首先介绍 ke，其可由公式 ke= π2γd2/6ρ［5］求得，当知道硅钢片密度、电导率及厚度后，即可得出;至此，式(4)可进一步表示为

按照式(5)所示，对实测损耗数据进一步处理，通过求解一个线性方程组即可求得系数kh和ke。此外，需要指出的是，除了上述介绍的损耗系数求解方法外，该模型中的系数还可以根据损耗实测数据直接拟合求得。

2.1.3算例

(1)文献［5］中通过研究8种铁磁材料的损耗特性，验证了该模型的适用性，同时对grain oriented three-percent SiFe铁磁材料进行了实测和计算损耗对比，指出当f≥50 Hz、磁密在1.5 T附近时，计算和实测损耗对比误差低于10%;

(2)文献［6］利用该模型，针对一台40 W，4极径向磁场无刷永磁直流电机，对两个不同牌号硅钢片和运行状态下的铁耗进行了计算;

(3)文献［7］计算了一台4极、37 kW直槽异步电机，实测利用热值试验(Calorimeter test)，计算得到空载铁耗为771 W，实测空载铁耗为756 kW;满载时计算铁耗为1 207 W，实测铁耗为1 362 W;

(4)文献［8］中利用该模型针对 3台2.2 kW、22 kW和132 kW电机，研究了斜槽对铁耗的影响。

(5)在国内利用该模型方面，也有众多文献利用该模型计算电机铁耗，例如文献［21-23］，所研究的电机包括异步电机、开关磁阻电机等多种，且各文献中计算和实测对比结果均显示能够很好地反映电机实际铁耗。受篇幅限制，不再详细列出其研究和计算结果。

2.2 常系数两项式模型

该模型即传统电机设计所采用的损耗计算模型，由磁滞和涡流损耗［2-3］两项组成，可表示如下:

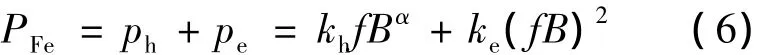
式中第一项为磁滞损耗，kh和ke分别为磁滞和涡流损耗系数;α为Steinmetz系数，上述三个系数均取决于材料特性，均通过对铁磁材料实测求得。需要指出的是，式(1)也是铁耗工程计算方法所采用的基本计算模型。该模型如式(1)所示，其损耗系数由硅钢片实测损耗数据拟合求得。该模型是电机铁耗工程计算方法中常用的一种，但是在利用有限元法计算电机铁耗时，该模型应用较少，故在此不对其作重点介绍。

3 基于有限元法的铁耗改进计算模型

前文介绍的常系数三项式计算模型虽然能够从一定程度上反映电机实际铁耗，但在某些特殊情况下其计算误差相对较高，例如文献［11］和［13］中指出常系数三项式模型的计算误差有可能达到30%以上。为了解决计算精度这一问题，学术界开展了大量理论和试验研究，其中部分学者在铁耗基本计算模型基础上提出了改进模型，以下将主要介绍铁耗有限元计算方法的一些改进模型，仅供参考。

3.1 变系数两项式模型

3.1.1 模型介绍

该模型由Mircea Popescu和Dan.M.Ionel于2007年提出，其表达式如式(1)所示。所谓变系数是指两个损耗系数kh和ke随磁密或频率变化。

3.1.2 模型中损耗系数求解

式(1)可进一步变形为

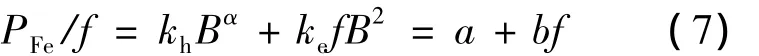
利用实测得到的损耗数据，即可得式(8):

对该式在某一频率下以B为变量进行拟合求解(可以取 1、2、3 阶曲线拟合)，如下［10-11］:

式(9)、(10)在同一频率下，需4～5个不同磁密点进行拟合得到系数 Ke0、Ke1、Ke2、Ke3、Kh、α0、α1、α2、α3后，即可得到任意频率和磁密下的损耗系数。

3.1.3算例

文献［10］中针对厚度为0.022英寸(0.5 mm)，相对磁导率为 3 071，P15/60为 3.16 W/Ib(1 Ib=0.45 kg)，密度为7 800 kg/m3的硅钢片，利用Epstein方圈对其进行了损耗测试，并建立相应模型计算上述硅钢片损耗。计算与实测对比误差在3%以内，同时和其他频率(并没有利用这些频率下的数据进行模型提取)下的铁耗对比误差也在5%以内。

3.2 变系数三项式模型

3.2.1 模型介绍

Dan.M.Ionel和Mircea Popescu等在文献［9-10］中，提出了变系数三项式计算模型，所谓变系数，是指式(2)中系数kh、ke和kα随磁密或频率变化。

3.2.2 模型中损耗系数求解

变系数三项式模型中的损耗系数求解方法和变系数两项式模型类似，求解过程中采用如下多项式:

在同一频率下，需对不同磁密点进行拟合，得到系数 Ke0、Ke1、Ke2、Ke3、Kh、a0、a1、a2、a3后，即可得到任意频率和磁密下的损耗系数。

3.2.3 算例

Dan.M.Ionel等于2007年在文献［9］中，利用变系数三项式模型，对三种硅钢片的实测和计算对比结果显示该模型误差在5%以内。同时以一台6极内置式永磁电机和一台4极异步电机为例，进行了实测和计算对比，结果如图2、3所示。

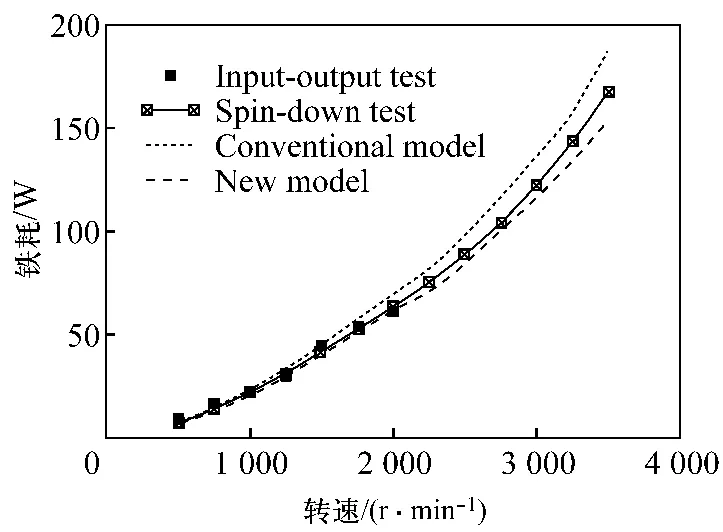
图2 内置式永磁电机空载铁耗的实测与计算对比［14］

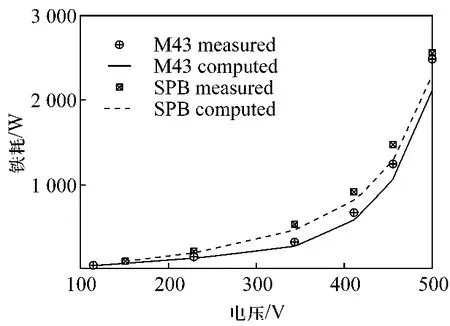
图3 采用两种硅钢片时异步电机铁耗的实测与计算对比［14］

3.3 铁耗的其他改进计算模型

3.3.1 磁滞损耗项改进模型

文献［12］和［13］中分别针对两项和三项模型中的磁滞损耗项，对Steinmetz系数α利用二阶多项式和三阶多项式进行拟合，分别表述如下:

式中:系数a、b和c的求解方法与前一小节类似。

3.3.2 涡流损耗项计及集肤效应的改进模型

Aldo Boglietti在文献［14］中，考虑了集肤效应对涡流损耗的影响。对常系数三项式模型进行了修正，其提出的模型如下:

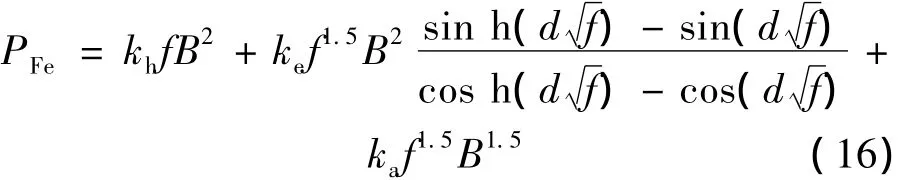
式中各系数求解方法与三项常系数模型类似。

3.3.3 一种基于Maxwell方程的涡流损耗模型

Zhang Yu在文献［24］中基于Maxwell方程建立了一种计及集肤效应的涡流损耗计算模型:

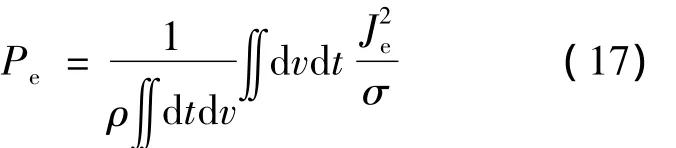
式中:Pe——单位质量和单位时间内的涡流损耗;

ρ——铁磁材料的质量密度;

Je——单元电流密度;

H——磁场强度;

B——磁通密度。

在式(17)基础上，文献［24］中还推导出恒定磁导率下计及集肤效应的涡流损耗解析表达式:

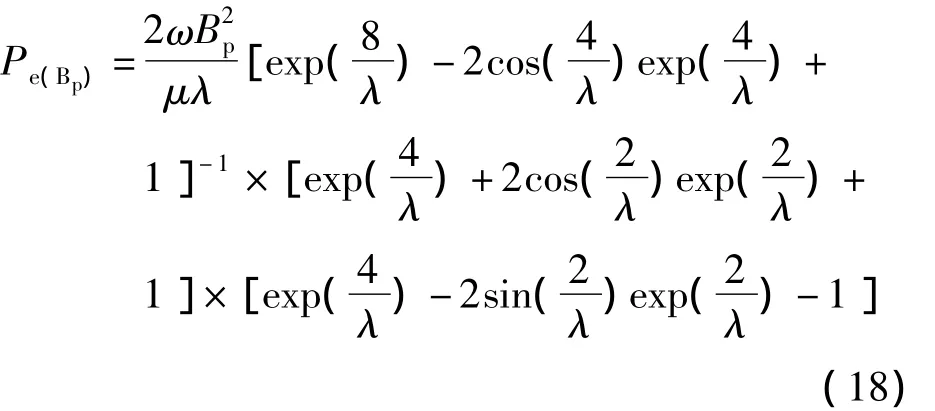
其中:λ =2δ/L;

L——材料厚度的一半;

δ——透入深度，δ=(2/ωμσ)－1/2;

ω——角频率;

μ，σ——磁导率，电导率;

Bp——磁密幅值。

关于式(18)应用范围，文献中指出其仅适用于磁密较低的情况，当磁密过高时，受磁导率变化的影响，该方法计算结果会有较大误差。

除了上述几种改进模型外，还有文献专门针对磁滞损耗提出了其他模型，例如F.Preisach提出的 Preisach 模型［25］、Hans Hauser提出的 Energetic模型［26］以及 Masato Enokizono 提出的 E＆S模型［27］等。受篇幅限制，此处不再详细介绍。

4 铁耗有限元计算方法的发展趋势及有待解决的问题

虽然基于有限元的铁耗计算方法已得到广泛应用，但综合文中内容可以看出现阶段存在众多模型，因此在计算模型对比、计算精度及实用性方面仍存在值得进一步深入研究的问题，总结如下。

(1)关于不同模型对比的研究:基于有限元方法的铁耗计算模型较多，因此应开展不同模型的对比研究。尽管已有文献开展了初步研究［28-30］，但其研究范围较小，且只是针对一台电机或一种运行状况研究，故该项工作需深入开展。

(2)在某些特殊应用场合，利用常系数模型计算精度较低，因此研究精度较高的变系数模型，是利用有限元法计算电机铁耗的必然发展趋势。

(3)建立更加适用于工程实际的有限元计算模型。文中介绍的模型均需要对材料实测损耗数据进行拟合求得，其数据处理过程繁琐且计算量大。工程中需要计算方法简单快捷的实用模型，因此研究基于有限元方法的铁耗计算实用模型也是下一步的重点工作。关于这方面，作者提出一种能够方便地应用于工程实际的铁耗完整计算模型，该模型包含了硅钢片损耗测试，模型建立、损耗系数求解及电机试验验证等完备流程，将另有文献专门提出。

［1］陈伟华，李秀英，姚鹏.中国中小型电机产业现状及发展趋势［J］.电机与控制应用，2008，35(2):1-7.

［2］波斯特尼柯夫.电机设计［M］.北京:机械工业出版社，1956.

［3］陈世坤.电机设计［M］.北京:机械工业出版社，2008.

［4］Kostas B Tatis，Antonios G Kladas，John A Tegopoulos.Harmonic iron loss determination in laminated iron cores by using a particular 3-D finite-element model［J］.IEEE Transactions on Magnetics，2004，40(2):960-963.

［5］Giorgio Bertotti.General properties of power losses in soft ferromagnetic material［J］.IEEE Transactions on Magnetics，1998，24(1):621-630.

［6］K Atallah，Z Q Zhu，D Howe.An improved method for predicting iron losses in brushless permanent magnet DC drives［J］.IEEE Transactions on Magnetics，1992，28(5):2997-2999.

［7］M A Mueller，S Williamson，T J Flack，et al.Calculation of iron losses from time-stepped finite-element models of cage induction machines［C］∥IEEE International Electric Machines and Drives Conference，Anterbury，UK 1995(9):88.

［8］Catherine I Mc Clay，Stephen Williamson.The variation of cage motor losses with skew［J］.IEEE Transactions on Industry Applications，2000，36(6):1563-1570.

［9］Dan M Ionel，Mircea Popescu，Stephen J Dellinger，et al.On the variation with flux and frequency of the core loss coefficients in electrical machines［J］.IEEE Transactions on Industry Applicantions，2006，42(3):658-667.

［10］Mircea Popescu，Dan M Ionel.A best-fit model of power losses in cold rolled-motor lamination steel operating in a wide range of frequency and magnetization［J］.IEEE Transactions on Magnetics，2007，43(4):1753-1756.

［11］Dan M Ionel，Mircea Popescu，Malcolm I McGilp，et al.Computation of core losses in electrical machines using improved models for laminated steel［J］.IEEE Transactionson Industry Applicantions， 2007， 43(6):1554-1564.

［12］Chen Yi Cheng，Pragasen Pillay.An improved formula for lamination core loss calculations in machines operating with high frequency and high flux density excitation［C］∥IEEE 37th IAS Annual Meeting，Pittsburgh，USA，2002(2):759-766.

［13］Tsakani Lotten Mthombeni，Pragasen Pillay.Physical basis for the variation of lamination core loss coefficients as a function of frequency and flux density［C］∥IEEE 32ndAnnual Conference on Industrial E-lectronics，Paris，France，2006(11):6-10.

［14］Aldo Boglietti，Andrea Cavagnino，Mario Lazzari，et al.Predicting iron losses in soft magnetic materials with arbitrary voltage supply:an engineering approach［J］.IEEE Transactions on Magnetics，2007，39(2):981-989.

［15］ASTM A343/A343M-03，Standard test method for alternating-current magnetic properties of materials at power frequencies using wattmeter-ammeter-voltmeter method and 25-cm epstein test frame［S］.2003.

［16］IEC 60404-2，Magnetic materials part 2:methods of measurement of magnetic properties of electrical steel sheet and strip by means of an epstein frame［S］.1996.

［17］GB/T 3655—2008，用爱泼斯坦方圈测量电工钢片(带)磁性能的方法［S］.2008.

［18］J D Lavers，P P Biringer，H Hollitscher.A simple method of estimating the minor loop hysteresis loss in thin lamination ［J］.IEEE Transactions on Magnetics，1978，14(5):386-388.

［19］J D Lavers，P P Biringer.Prediction of core losses for high flux densities and distorted flux［J］.IEEE Transactions on Magnetics，1981，12(6):1053-1055.

［20］Hideo Domeki，Yoshiyuki Ishihara，Chikara Kaido，et al.Investigation of benchmark model for estimating iron loss in rotating machine［J］.IEEE Transactions on Magnetics，2004，40(2):794-797.

［21］赵海森，刘晓芳，罗应立，等.电压偏差条件下笼型感应电机的损耗特性［J］.电机与控制学报，2010，14(5):13-19.

［22］安忠良.超高效永磁同步电动机研究开发［D］.沈阳:沈阳工业大学，2006.

［23］程树康，裴宇龙，张鹏，等.旋转电机第三功能初探［J］.电工技术学报，2007，22(7):12-17.

［24］Yu Zhang，Rui Guan，Pragasen Pillay，et al.General core losses models on a magnetic lamination［C］∥IEEE Conference on Electric Machines and Drives，Miami，USA，2009(3):1529-1534.

［25］Preisch F.Uber die magnetische nachwirkung［J］.Zeitschrift Fur Physik，1935(94):277-302.

［26］Hans Hauser.Energetic model of ferromagnetic hysteresis:isotropic magnetization［J］.Journal of applied physics，2004，96(5):2753-2767.

［27］Masato Enokizono，Hiroyasu Shimoji，Toyomi Horibe.Loss evaluation of induction motor by using magnetic hysteresis E＆S2Model［J］.IEEE Transactions On Magnetics，2002，38(5):2379-2381.

［28］Carlos A Hernandez-Aramburo，Tim C Green，Alexander C Smith.Estimating rotational iron losses in an induction machine［J］.IEEE Transactions on Magnetics，2003，39(6):3527-3533.

［29］Oriano Bottauscio，Aldo Canova，Mario Chiampi，et al.Iron losses in electrical machines:influence of different material models［J］.IEEE Transactions on Magnetics，2002，38(2):805-808.

［30］Emad Dlala.Comparison of models for estimating magnetic core losses in electrical machines using the finite-element method ［J］.IEEE Transactions on Magnetics，2009，45(2):916-925.