基于磁路交叉饱和及电感参数补偿的内置式永磁同步电机解耦控制

王艾萌， 石文娟

(华北电力大学电气与电子工程学院，河北保定 071003)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有能量密度高、效率高、可靠性高、体积小、结构简单等优点，其在航空航天、数控加工、电动汽车驱动等领域已得到了广泛应用［1-3］。根据永磁体在转子侧安装位置的不同，可将电机分为表面式PMSM和内置式PMSM(Inner PMSM，IPMSM)。IPMSM存在磁阻转矩，提高了恒转矩区的转矩输出能力，并且拓宽了恒功率区的速度运行范围，更符合电动汽车使用要求。

PMSM是一个多变量、强耦合、非线性的系统，交叉饱和、耦合等多种因素的影响使电机的控制性能和精度不理想［5］。本文在对考虑饱和的电机参数和PMSM的数学模型分析的基础上，利用MATLAB建立了具有饱和特性的电机模型。采用每安培最大转矩和弱磁控制策略，在调速控制系统加入跟随电机参数变化的解耦控制模块，实现考虑饱和补偿的优化控制，并与没有饱和补偿的控制系统模型进行比较。最后，基于MATLAB建立系统仿真模型，仿真结果表明改进后的系统具有较快的响应时间，拓宽了高速区的范围，提高了低速区的输出转矩。

1 IPMSM数学模型

以坐标旋转变换为基础的PMSM矢量控制，在dq同步旋转坐标系下实现了类似直流电机的控制性能。其稳态运行时的数学模型等效方程如下。

电压方程:

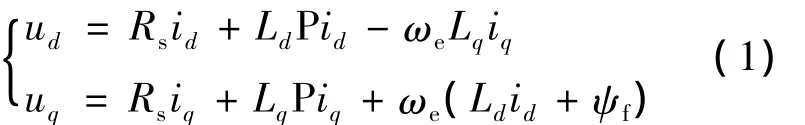
转矩方程:

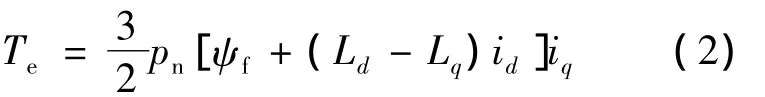
在稳态下，id、iq为常数，高速时，电阻压降可以忽略，电压方程可简化为

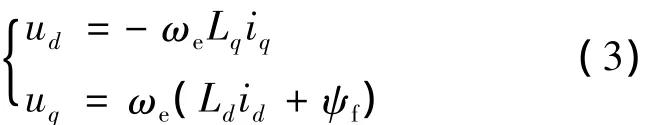
式中:ud、uq——d、q 轴的等效电压;

Rs——定子电阻;

id、iq——d、q 轴电流;

Ld、Lq——d、q 轴电感;

P——微分算子;

pn——极对数;

we——电角速度;

Ψf——永磁磁链;

Te——电磁转矩。

2 电流控制策略

为了充分利用磁阻转矩，IPMSM运行在恒转矩区，采用每安培电流最大转矩控制策略。该方法可使逆变器的输出电流最小，减小了逆变器和电机的损耗，降低了系统的整体损耗，节约了能量;并且可以顺利过渡到弱磁控制，改善电动机恒功率运行时的输出转矩性能。随着速度的提高，电压随之增加，当电机转速升到转折转速时，转矩输出最大且电压电流均达到极限值，此时，电机运行在如图1所示的A点。

若电机继续升速，则进入到弱磁运行区域。根据弱磁控制(Flux-Weakening)原理，通过增加去磁电流Id，减小直轴磁链来维持高速运行时电压平衡，达到弱磁扩速的目的。弱磁控制可分两种方式:(1)如图1所示，电机在A点时输出最大转矩，若升速则以减小转矩为代价，电流轨迹沿电流圆逆时针方向向下，即为AC段运行轨迹;(2)如果电机没有达到最大转矩时(如D点)进入到弱磁状态，则电机可以恒转矩运行到F点，若继续提高转速，则转矩随之降低，沿FC段轨迹运行。CE段为最大功率弱磁区域，只有电机的弱磁率ξ=Ldis/ψf＞1时才存在，理论上速度可以达到无穷大，此时输出转矩为零。

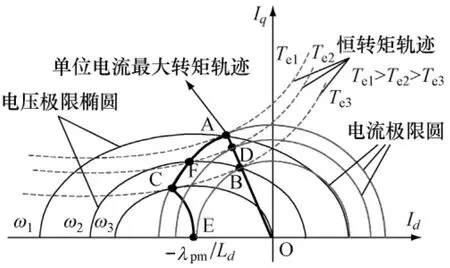
图1 定子电流矢量轨迹

3 磁路饱和影响及电感参数补偿

在IPMSM中，有效气隙小，电枢反应磁场的作用使磁阻发生很大变化，d轴电感和q轴电感不相等，转子结构不对称，存在磁路交叉饱和影响。由于d轴位于永磁体的轴向位置，如图2所示，且永磁体的磁导率接近于空气磁导率，所以q轴的有效气隙比d轴有效气隙小，因此电枢反应引起的磁饱和主要存在于q轴。根据有限元软件分析得到的d、q轴电感随电流的变化如图3所示，d轴电感值相对稳定，q轴电感值随q轴电流增加而明显减小。

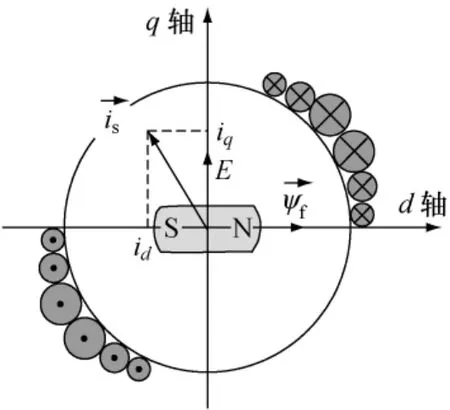
图2 电流矢量图

由于q轴电流与转矩成线性关系，在恒转矩区，交叉饱和作用使q轴电感变小，凸极率下降，所以电机输出转矩因饱和作用也会降低。在低速运行区，采用每安培电流最大转矩控制策略，电机的电感参数分别采用额定运行的恒值和图3所示的电感随电流变化的非线性值。电机转矩和机端电压输出曲线如图4所示，可以看出磁路交叉饱和对电机特性的影响，考虑交叉饱和时电机输出转矩和机端电压均降低，因此需要对电机的饱和影响进行补偿。

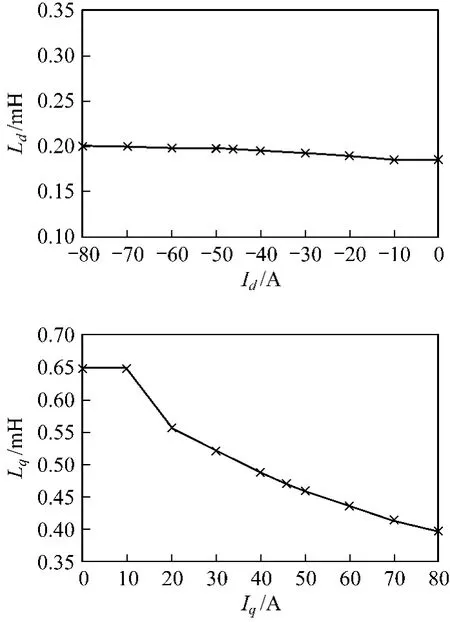
图3 电感随电流变化曲线

在高速区，即弱磁区域，由于电流圆的限制，随着去磁电流Id的增加，Iq不断减小，磁饱和作用降低。但是，随着d轴电流的不断增大，d轴电感值略有下降，凸极率增加，则电机的转矩输出能力略有提高。

为了更好地发挥电机固有的输出能力，在控制系统中利用插值法进行补偿。考虑饱和补偿和没有考虑饱和补偿的转矩速度特性曲线如图5所示。从图中可以看出考虑补偿的控制方式不但拓宽了高速区运行范围，还提高了电机输出转矩。

4 电流解耦环节

由式(1)可看出d轴和q轴反电动势相互耦合，即 ud、uq不能独立控制 id、iq，属于典型的非线性系统。由式(1)可知，在低速时，耦合影响小，而在高速时，由于IPMSM的自感相对较大，耦合起了主导作用，使得耦合影响随着转速的提高更加明显，从而严重影响弱磁电流和转矩响应。要独立控制id和iq，需采用前馈方式对 id和 iq解耦，如式(4)所示。

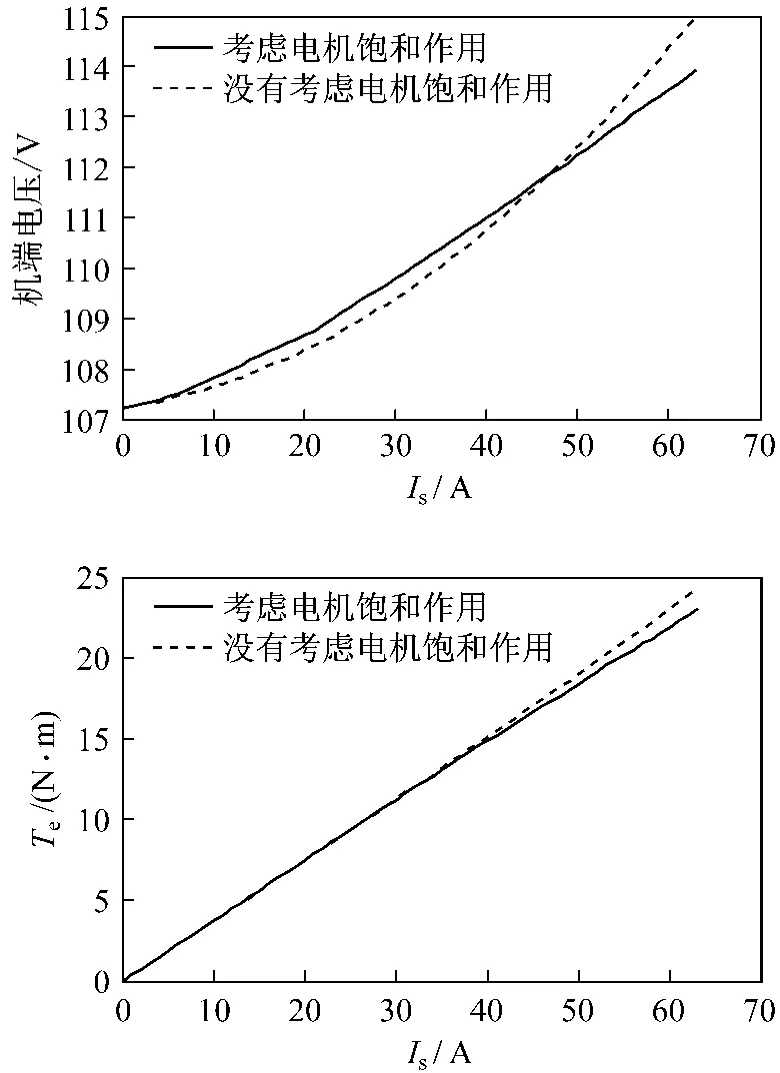
图4 采用每安培电流最大转矩电流控制策略的机端电压和转矩比较

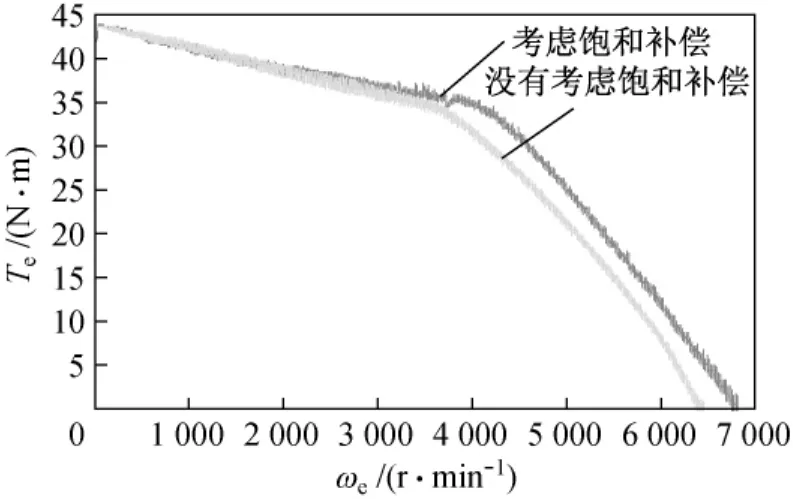
图5 考虑参数饱和补偿和没有补偿时的转矩速度特性比较

udec、uqec——解耦后得到的参考电压。

在有些运行状态下，解耦之后控制系统性能并不完美，电机饱和也会对控制系统带来不稳定的影响。在高速时，若假设q轴电感为恒定值，当电流指令变化较大时，由于电机和逆变器的容量有限，会使得机端电压超过极限值，PI控制器的输出产生电压饱和现象，使得控制系统不稳定。因此，采用了电感变化的前馈解耦控制方式对给定电压进行补偿，解耦控制模块如图6所示。

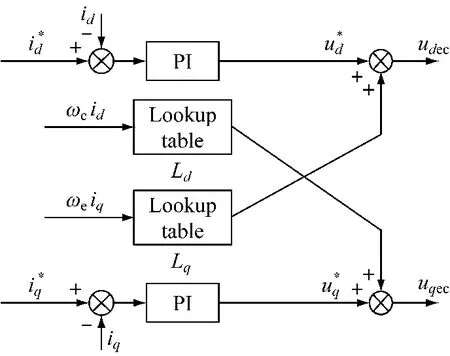
图6 采用参数补偿的解耦模块

5 结果分析

PMSM矢量控制系统框图如图7所示。为了模拟实际的电机模型，在此控制系统中，建立了考虑参数饱和特性的电机模型，并在控制系统中，利用跟随电机参数变化的解耦模块对电机电压饱和的影响进行了补偿控制。电机参数如表1所示。

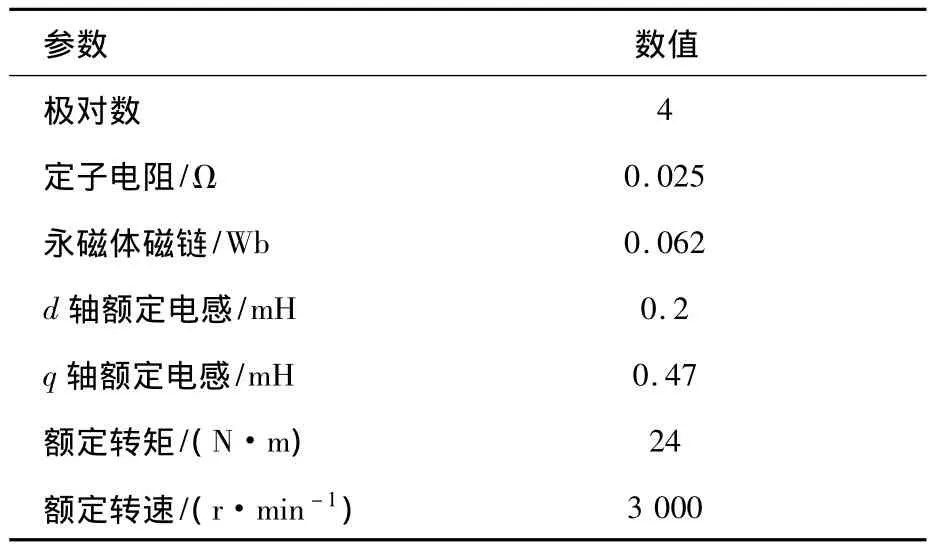
表1 7.5 kW电机参数

利用MATLAB对电机调速系统进行了仿真，并对有、无解耦补偿的控制系统仿真结果进行比较，如图8所示。电机空载起动，达到给定速度4 000 r/min后，在t=0.15 s加小负载转矩Te=5 N·m，电机稳定运行后在t=0.2 s时转速阶跃上升到5 000 r/min。如图8(a)所示，采用解耦补偿之后，电机的起动转矩大，起动时间短，响应速度快，转矩波动小。图8(b)为速度曲线，解耦补偿之后转速快速上升到给定值，加负载扰动，速度稍有降低后立即恢复到稳定值，动态性能好，鲁棒性好。图8(c)、(d)为电流响应波形，电流波动小，抗干扰性好，能快速稳定。

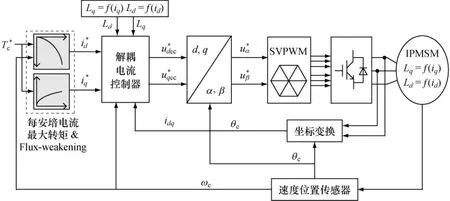
图7 IPMSM调速控制系统框图

6 结语

为了模拟实际电机运行状态，本文建立了考虑电机参数饱和特性的PMSM模型，在控制系统中采用了跟随电机参数变化的解耦控制算法，拓宽了弱磁区速度运行范围，提高了恒转矩区输出转矩，解决了高速区电机机端电压超过限制电压而产生的控制系统不稳定问题，同时提高了控制系统动态性能、鲁棒性和控制精度。

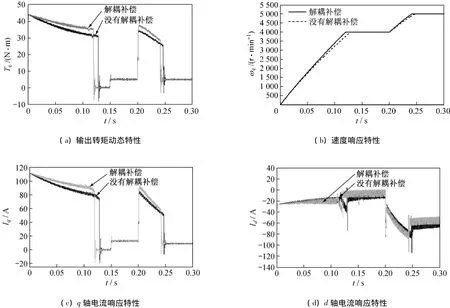
图8 IPMSM控制系统考虑解耦补偿和没有补偿时输出特性比较

［1］Emil Levi，Member，Viktor A Levi.Impact of dynamic cross-saturation on accuracy of saturated synchronous machine models［C］∥IEEE Transactions of Energy Conversion，2000(15):224-230.

［2］Hyunbae Kim，R D Lorenz.Improved current regulators for IPM machine drives using on-line parameter estimation［C］∥IEEE Trans Ind Appl，2000(1):86-91.

［3］Sneyers B，Novotny D W，Lipo T A.Field-weakening in buried permanent magnet AC motors drives［C］∥IEEE Trans on Ind Appl，1985(IA-21):398-407.

［4］Jahns T M，Kliman G B，Neumann T W.Interior permanent-magnet synchronousmotorsforadjustablespeed drives［C］∥IEEE Trans on Ind Appl，1986(2A-22):738-747.

［5］Shigeo Morimoto，Masayuki Sanada，Yoji Takeda.Effects and compensation of magnetic saturation in flux-weakening controlled permanent magnet synchronous motor drives［C］∥IEEE Transactions on Industry Applications，1994(30):1632-1637.

［6］Park J W，Koo K H，Kim J M，et al.Improvement of control characteristics of interior permanent magnet synchronous motor for electric vehicle［J］.Rec of Ind Appl Soc Ann Mtg，Rome，2000:1888-1895.

［7］Kang G H，Hong J P，Kim G T，et al.Improved parameter modeling of interior permanent magnet synchronous motor based on finite element analysis［J］.IEEE Trans Ma，2000(36):1867-1870.

［8］Edward C Lovelace，Thomas M Jahns，Fellow，et al.Impact of saturation and inverter cost on interior PM synchronous machine drive optimization［J］.IEEE Transactions on Industry Applications，2000(36):723-729.

［9］Bojan Stumberger，Gorazd Stumberger，Drago Dolinar，et al.Evaluation of saturation and cross-magnetization Effects in interior permanent-magnet synchronous motor［J］.IEEE Transactions on Industry Applications，2003(39):1264-1271.