基于三电平中点钳位式拓扑的中压风电变流器

高 宁， 蔡 旭， 张 亮， 罗悦华

(上海交通大学电气工程系，上海 200240)

0 引言

能源问题是当今人类社会面临的重要问题之一，对可再生能源的开发利用，特别是对风能的开发利用，已受到世界各国的高度重视［1］。从今后的发展趋势来看，风电场建设重点将从内陆移向海上，以求得更广阔的发展空间。海上机组的容量比陆地机组更大，可达3 MW以上。在这样的功率等级下，若采用传统低压电机加低压变流器方案，则电流过大引起的损耗将会成为限制风机容量增加的瓶颈。若要减小损耗，就必须加粗铜线，而这又会大大增加系统成本和施工难度，可见传统方案陷入了两难境地。为突破这一瓶颈，唯一的出路就是提高系统的电压等级。因此，将中高压变频技术应用到风电变流器中，在理论与实践上都非常有意义，开发具有中压变频器拓扑的多电平风电变流器是提高系统效率的有效途径。

常见的多电平变流器拓扑大致可分为:二极管钳位型［2］(NPC)、H桥级联型、飞跨电容型、混合钳位型等。其中二极管中点钳位型多电平变流器近年来在高压电机驱动、无功功率补偿等领域得到了广泛应用。因此，本文针对该拓扑进行了研究，全功率风电变流器的主要结构如图1［3］所示。

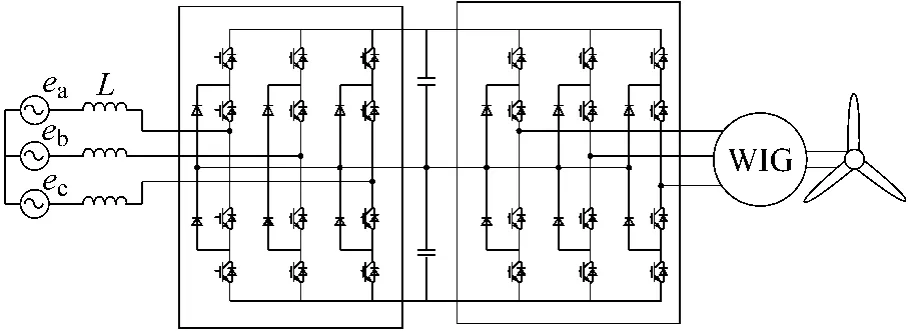
图1 基于背靠背三电平NPC的中压风电变流器基本结构

1 风电变流器的控制策略

1.1 网侧变流器的控制策略

若将网侧变换器的后侧电路等效为一个负载电阻RL，则网侧变换器可表示为图2。

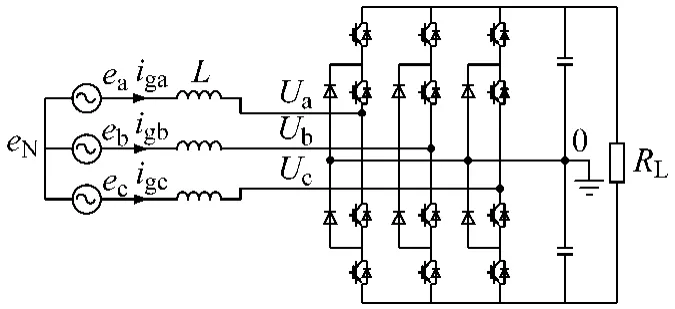
图2 网侧变换器的等效模型

取图中的O点即电容中性点为参考点，记变换器的输出电压为 Ua，Ub，Uc，电网频率为 ω，忽略器件导通电阻，可以得到网侧变换器的数学模型如下［4］:

将式(1)变换到dqo旋转坐标系下，可化为

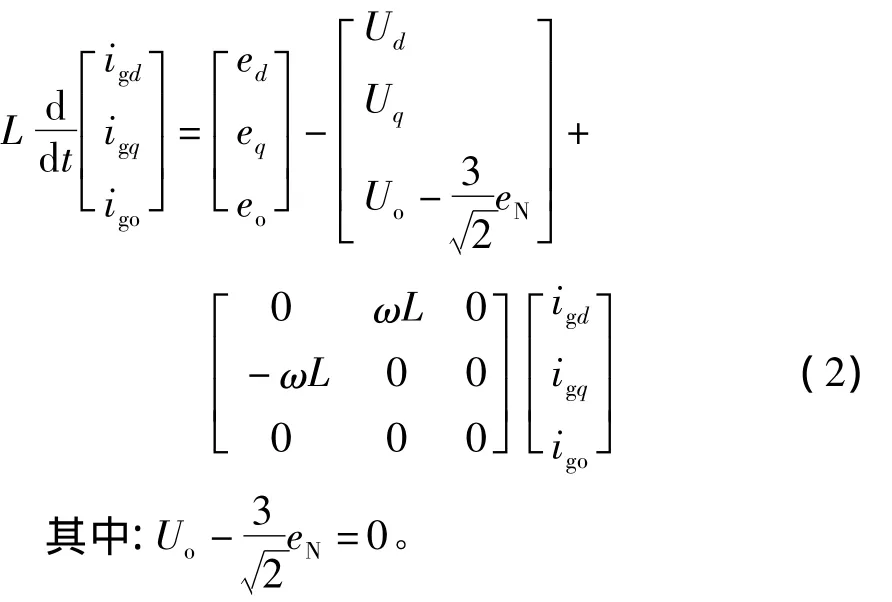
根据式(2)，通过对Ud、Uq的控制可以分别控制变换器的igd和igq，而零轴电流则可略去。为使电流快速跟踪给定电流，电流内环采用PI控制，可令:

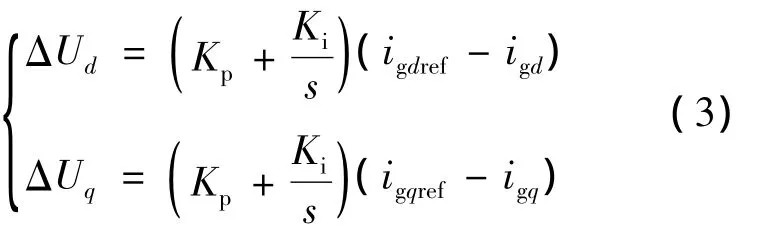
输出至调制部分的电压给定为

即可通过电压电流反馈解耦实现电流内环的igd，igq的解耦控制。

若将dq旋转坐标系的d轴定位于两相静止坐标系中电网电压矢量方向，则可得eq=0。为使d轴定向于电网电压矢量方向，在实际控制中通常采用锁相环技术(PLL)得到对应的变换角θ。

网侧变流器的最终控制目的是使直流母线电压稳定以实现功率的动态平衡。为达到这一目的，可采用电压外环PI控制。将两个电容电压作为一个整体进行控制，给定电压Udcref与实际电压Udc相减，经过PI调节器得到d轴电流的给定值idref。综上可得网侧变换器的整体控制框图如图3所示。

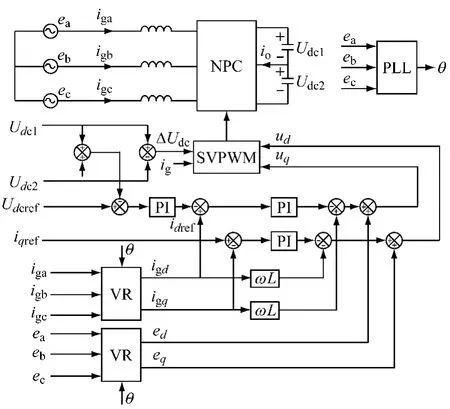
图3 网侧变流器的控制策略

1.2 机侧变流器的控制策略

在理想条件下，基于转子磁链定向的旋转mt坐标系中的异步电机模型可表达如下［5］:

式中:np——电机极对数;

Lm——定转子互感;

ω1，ω——同步速及电机转速;

ψr，Lr——转子磁链及电感;

Tr——转子电磁时间常数;

ism，ist——m 轴和 t轴电流。

根据上述数学模型，可以认为转子磁链仅由定子电流励磁分量ism产生，由式(6)，ψr与ism之间的传递函数是一阶惯性环节，其时间常数即为Tr。因此，定子电流励磁分量的突变并不会引起转子磁链的突变，转子磁链ψr易于控制。根据式(6)，在稳态下 dψr/dt=0，可得 ψr=Lmism，即在控制系统中可令ismref=ψr/Lm，以实现磁链的开环控制。由于磁链是难以精确观测的，因此采用磁链开环控制简化系统，在精度上不会太差。

尽管数学模型已被大大简化，但转矩和磁链两个子系统还是耦合在一起的，比较简单的解耦方法是将转矩给定除以磁链，即令istref=TerefLr/(npLmψr)，以实现两个子系统的解耦。另外，根据机械运动方程，当电磁转矩大于负载转矩时，电机转速上升，反之则下降。因此，可以将转速给定减去当前转速，通过一个PI调节器得到转矩给定(称为转速调节器)。由于一般情况下电机均工作在发电状态，因此转矩给定恒为负值，阻碍转子转动。为防止电机工作在电动状态，可对转速调节器的输出上限进行设置。综上可得异步电机磁链开环的矢量控制框图如图4所示。

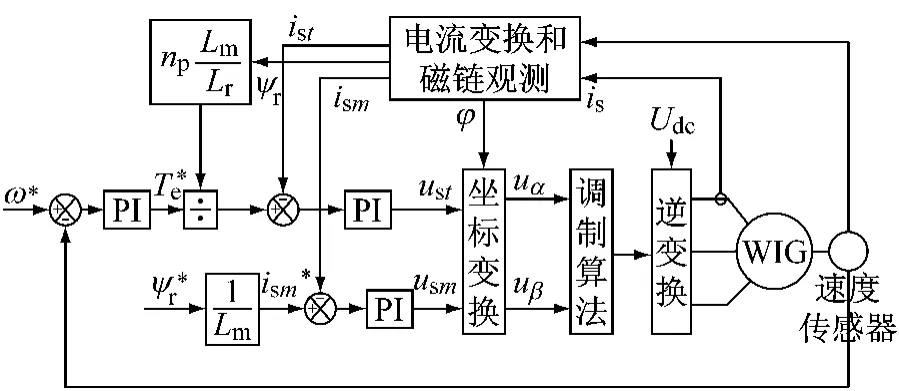
图4 异步电机的矢量控制

2 三电平NPC的空间矢量调制

2.1 三电平NPC的空间矢量脉宽调制算法

关于两电平变换器空间矢量调制的研究已经很成熟，在其基础上进行推广即可得到三电平NPC的空间矢量调制算法。三电平NPC共有27个矢量，在αβ平面上的分布如图5所示。

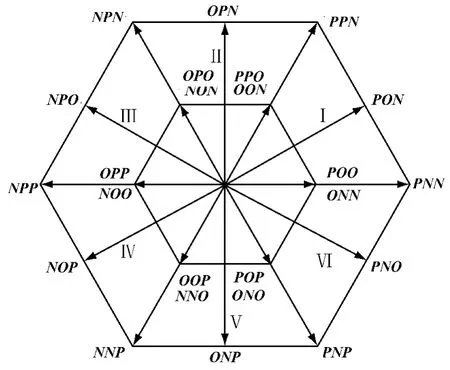
图5 三电平NPC的电压空间矢量

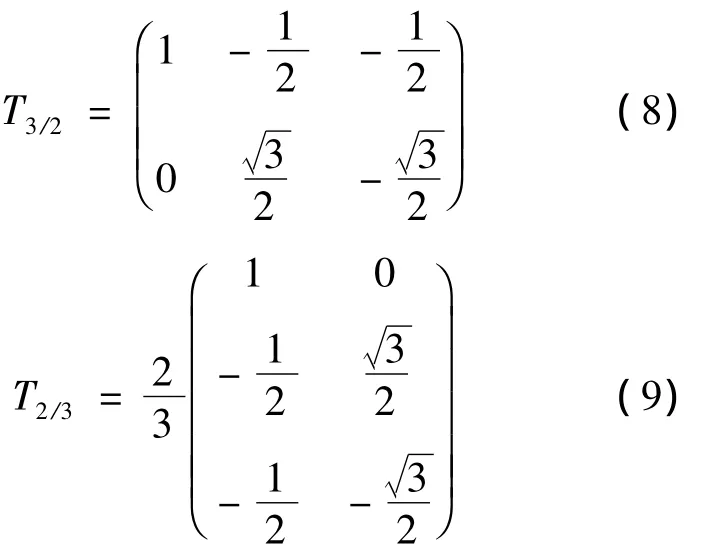
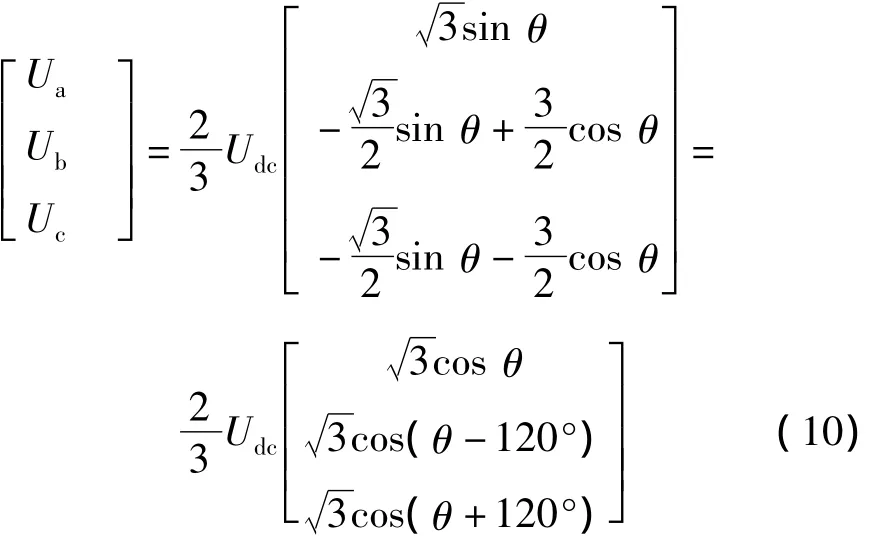
表1 矢量分类

根据图5，整个αβ平面可以被分为六个大扇区，为方便叙述，从α轴开始，按逆时针顺序将其分别命名为扇区Ⅰ～Ⅵ。每个大扇区中的空间结构具有高度的相似性，因此为简化计算，可以通过线性变换将所有扇区映射至第一扇区进行求解。即可以只考虑第一扇区中矢量分配时间的计算，而别的五个扇区只需在矢量发送顺序上作相应调整，下面叙述第一扇区中矢量分配时间的计算。如图6所示，第一扇区可以被分为4个区域，其中的A区、B区又被PON矢量分割为两个小区域，矢量所在区域可根据表2判定。判定了矢量所处区域之后，即可计算矢量的分配时间，以区域D为例，根据伏秒平衡原理，设开关周期为Ts，可得:

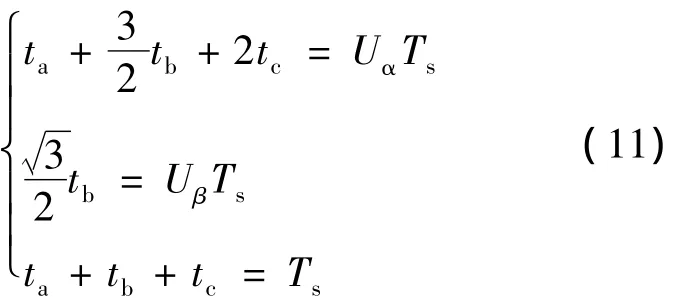
解得:

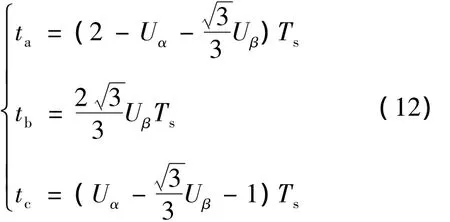
同理可得第一扇区中各小区域中矢量的时间分配(见表3)。在得到了ta，tb，tc之后，还需要确定矢量的发送顺序。本文采用的是首发小矢量全部为正小矢量，与之等效的负小矢量居中的发送顺序。

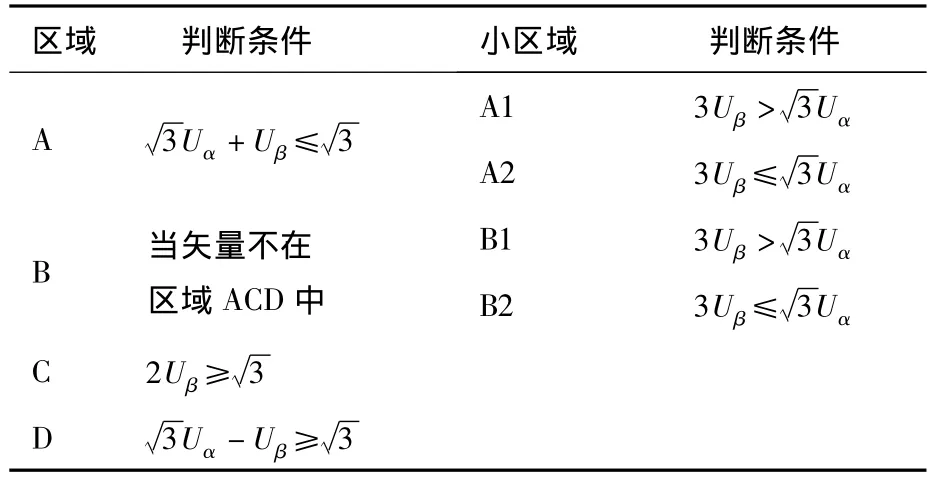
表2 区域划分及其判断条件

2.2 三电平NPC的中点电位平衡

由于三电平NPC拓扑的特殊性，中线上会有电流流过，其上下电容会产生分压不均的情况，造成中性点电压的偏移，需要尽量避免。从空间矢量的角度看，上下电容电压波动的原因如下:当变换器输出诸如PNN这类长矢量时，上下电容通过各自正负端与电网侧构成回路，不存在问题。当变换器输出中矢量时，如图7(a)所示，此时中线电流io=ib，若 ib大于零，则 Udc1下降，Udc2上升。由于中矢量的非冗余特性，因此由中矢量引起的电容电压波动是无法避免的，但可以通过对正负小矢量时间分配的调整尽量抑制中点电位的波动。与中矢量的分析方法类似，在变换器输出小矢量时，以POO、ONN为例，如图7(b)、(c)所示。

图7 中点电位波动的简单分析

当变换器输出正小矢量时，上电容的充放电电流为ia;当变换器输出负小矢量时，下电容的充放电电流为－ia。当ia为正且Udc1＞Udc2时，适当延长正小矢量的作用时间便可使Udc1和Udc2趋于平衡，反之亦然。据此，可以得到一种基于小矢量作用时间重配置的中点电位模糊控制方式，具体方法如下。

根据前文所述得到矢量分配时间ta，tb，tc之后，将正小矢量的作用时间调整为ta/2+KΔt，负小矢量的作用时间调整为ta/2－KΔt(K为调整因子)。其中Δt的取值如表4所示，即可对中点电位进行控制。表中:ΔUdc=Udc1－Udc2;θ为合成矢量与α轴的夹角;sgn代表取符号函数。

表3 矢量分配时间与发送顺序(第一扇区)

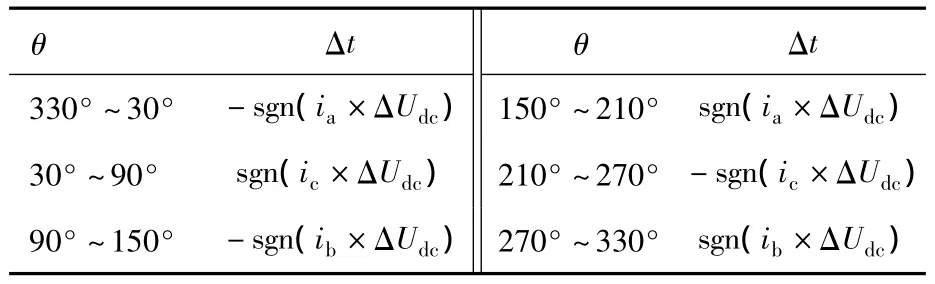
表4 Δ t的取值

3 仿真分析

根据前文的理论分析，在MATLAB/Simulink中建立了完整的基于三电平NPC的风电变流器模型。具体仿真参数如表5所示。

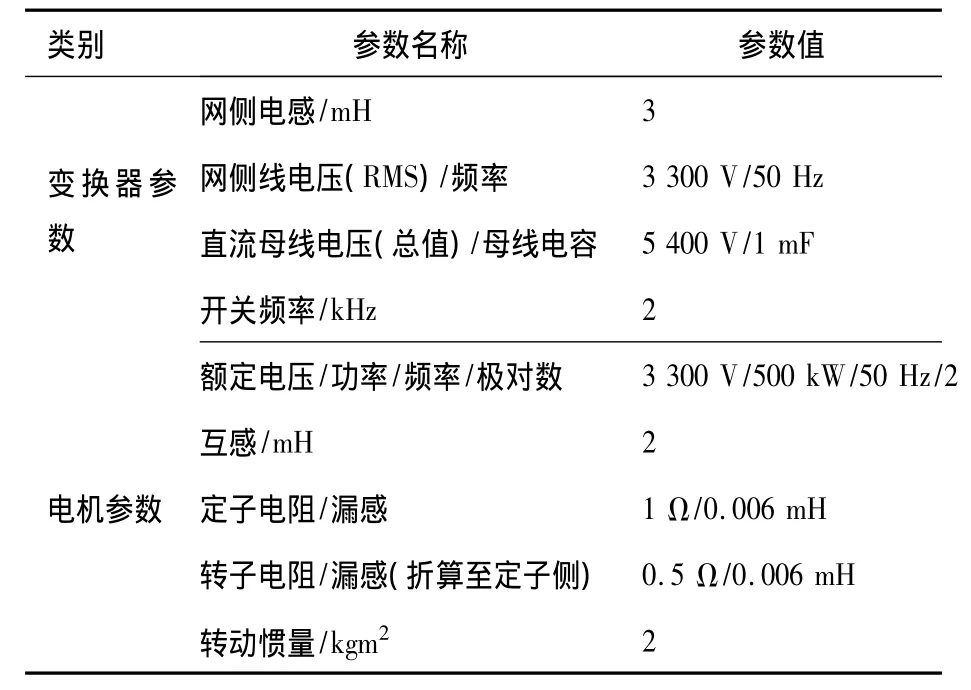
表5 仿真参数

风机模型使用MATLAB/Simulink中的已有模块，设定风机机械功率基值为400 kW，为发电机功率的80%，风速达到13 m/s时，风机机械功率达到满功率值，风速约为14 m/s时，发电机达到额定功率值。风机的机械特性如图8所示，额定风速为10 m/s，额定转速157 rad/s(1 500 r/min)。仿真波形罗列于图9中。风速为10 m/s时的仿真波形见图9(a)～(j)，从图9(a)、(b)可以看出，发电机的控制良好，成功实现了转速的闭环控制，使发电机工作在给定转速157 rad/s(1 500 r/min)附近。图9(c)、(d)给出了网侧变流器独立控制中点电位时的直流侧电压波形，从中可以看出上下电容电压基本相等，基于小矢量作用时间重配置的中点电位模糊控制方式简单有效，三电平NPC的中点电位得到了很好的控制。图9(g)～(j)表示网侧变换器向电网输出功率稳定，dq轴电流能够精确跟踪给定，电流波形接近于正弦，谐波含量小(THD=1.99%)，相电流与相电压反相，功率因数接近于－1。

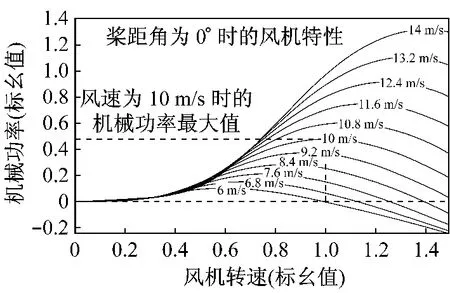
图8 风机的机械特性

图9 仿真波形

由图8可见，风机在每个风速下都有其功率最大点，机侧变换器的控制目标就是要将发电机的转速控制在功率最大点对应的转速下以达到最大风能捕获的目的。图9(j)为在不同风速下系统输出功率的仿真结果，基本与图8一致，证明了稳态情况下下机侧变换器可以完成不同风速下的最大功率跟踪。由于风能是一种不稳定的能源，风速随时间有较大波动，为简化分析，假设风速近似按式(13)波动［7］，以验证在风速动态变化时能够实现最大风能跟踪。

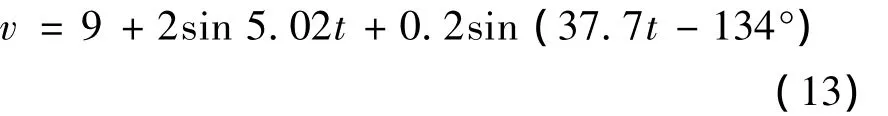
仿真结果见图9(k)，从中可看出风速在一定范围内波动时，电机转速也能很好地跟随其变化以实现最大风能跟踪。与稳定风速下的情况相比较，直流侧电压(图9(l))的波动变得更大，但尚在可以接受的范围内。

4 结语

本文对中高压变频技术在风电变流器中的应用进行了初步研究，对背靠背三电平中点钳位式拓扑在中压风电中的应用进行了仿真分析。为提高直流电压利用率，本文采用了三电平空间矢量脉宽调制算法，并且对该拓扑电容分压不均的固有缺陷进行了分析，采用了一种基于调整小矢量时间分配的算法抑制中点电位波动。通过MATLAB/Simulink的仿真，验证了控制算法的正确性。仿真结果说明将中高压变频技术应用到风电变流器中是可行的，这将为今后的实践工作作出理论指导。

［1］叶杭冶.风力发电机组的控制技术［M］.北京:机械工业出版社，2006.

［2］Nabae Akira，Takahashi Isao，Akagi Hirofumi.A new neutral－point－clamped PWM Inverter［J］.IEEE transactions on industry applications，1981，IA－17(5):518－523.

［3］杨勇，阮毅，张朝艺，等.基于背靠背三电平电压变换器的直驱式风力发电系统［J］.电网技术，2009，33(18):148－155.

［4］徐德鸿.电力电子系统建模及控制［M］.北京:机械工业出版社，2005.

［5］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2003.

［6］Knight A M，Peters G E.Simple wind energy controller for an expanded operating range［J］.IEEE transactions on energy conversion，2005，20(2):459－466.