中央与地方关系的一般信号博弈模型分析

栾贵勤 沈科英 庄 毅

（上海理工大学 管理学院，上海 200093）

中央与地方关系的一般信号博弈模型分析

栾贵勤 沈科英 庄 毅

（上海理工大学 管理学院，上海 200093）

中央与地方的利益关系是两者之间关系的核心内容。双方对利益最大化追求的过程，就是一个博弈的过程。中央政府的倾向是一种信号，地方政府在接收到特定的信号后，根据这一信号来判断中央政府的态度，最后决定自己的行动。因此，本文将中央政府与地方政府的关系定义为两方多阶段有限重复博弈，选用经典博弈论中的信号博弈模型对中央政府与地方政府的行动进行分析，求得一般均衡解。

中央与地方关系；信号博弈；精炼贝叶斯均衡

中央与地方的关系自古有之，但不同时期其具体的表现形式各异。随着改革的深入，中央与地方政府的矛盾开始加剧：中央政府的许多政策出台后， 地方政府并不认真执行。上有政策，下有对策。二者的博弈陷入白热化。中央与地方存在着一定的博弈关系， 其利益关系构成了两者之间关系的核心内容。

一、信号博弈模型的表述

从经典博弈论的角度看，中央与地方的关系存在着某种信念的更新和完美性。将中央政府和地方政府看作各自独立（不完美信息）的实体，中央政府的行动（收益最大化的行动）受自身类型（如政策倾向等）的控制，并会向处于行动下方的地方政府发出某种对其类型有所暗示的信号；地方政府在接受到行动上方的信号后，通过经验或已有知识判断中央政府的类型，进而选择收益最大化的行动以应对。现实中，中央政府对行动的选择和地方政府对中央政府类型判断的修正是持续进行的，整个进程符合基本的信号传递博弈，两者无论在经济政策的推行还是在行政干预等领域的行动都可以归纳为信号博弈模型的策略选择问题。因此，本文将中央政府与地方政府的关系定义为两方多阶段有限重复博弈，选用经典博弈论中的信号博弈模型对中央政府与地方政府的行动进行分析，求得一般均衡解。

二、信号博弈模型的建立及求解

假设中央政府的类型θ分布于类型集合Θ上，并对自身类型具有私人信息，行动a1分布于行动集合A1上，中央政府（C）的策略规定其类型θ在行动a1上的概率为σ1(a1/θ)；地方政府（L）的行动a2分布于行动集合A2上，其策略规定相对于中央政府的每一种行动a1在行动a2上的概率为σ2( a2/ a1)。中央政府对地方政府策略选择判断的概率为γ(θ)，地方政府对中央政府类型判断的后验概率为µ(θ/a1)。那么在一期选择中，中央政府的预期收益u1和地方政府的预期收益u2分别是：

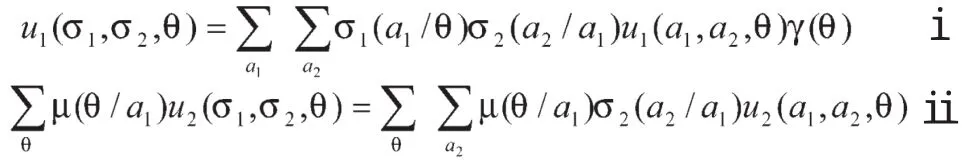
以环境保护领域为例，假设参与方中央政府和地方政府都具有有限理性，那么中央政府（C）的类型可以归纳为两类：追求环境保护与经济收益的可持续发展（E），片面追求经济收益（G）。同样，地方政府的行动也可以分为这两类。由于中央政府和地方政府的特质，中央政府对两种类型的概率分布趋向均分，而地方政府更趋向于对高经济收益的追求。用D、P分别表示中央政府和地方政府的收益（社会收益和经济收益的总和），那么两方信号博弈树可以用图1表示。

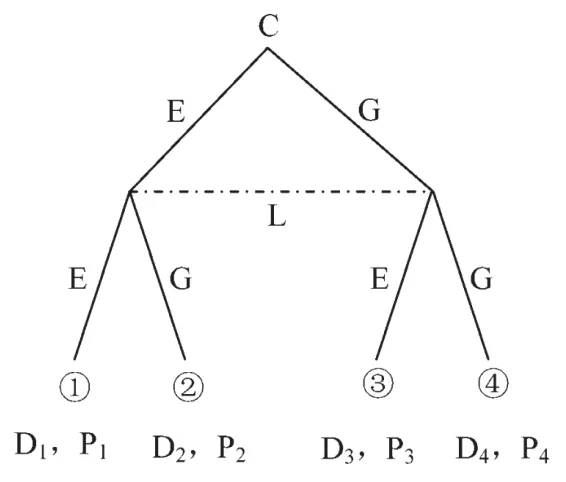
图1 信号博弈树

在这里，参与方的类型决定了经济收益和社会收益对其显示价值的大小，当参与方的类型为追求可持续发展时，会认为牺牲部分经济收益提高社会收益后的总收益更大，反之亦然。因此存在以下关系：

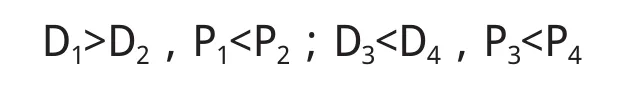
在博弈开始前，参与方的信息是不完美的，但是会通过不断重复增加经验。为简化起见，将信号博弈分为两期，两期间的贴现因子为ε。下面分析模型的四个解。

（1）当C的类型为E。

第一期：L接受到C的信号，选择策略E，两方收益分别是D1，P1。

第二期：L仍然选择策略E，两方的收益是εD1，εP1。

综合两期的最终收益，C的总收益是D1+εD1，L的总收益是P1+εP1。

（2）当C的类型为E。

第一期：L根据自身的倾向选择策略G，两方的收益是D2，P2。

第二期：L根据第一期的结果，如C对L的行政干预等，对C的类型进行修正，选择策略E，两方的收益是εD1，εP1。

综合两期，C的总收益是D2+εD1，L的总收益是P2+εP1。

小结：对C的类型为E时两方总收益的讨论。

中央政府（C）在情形（1）和（2）中总收益的差别是：②-①=

因此，C更倾向于情形（1）的结果。

地方政府（L）在情形（1）和（2）中总收益的差别是：②-①=

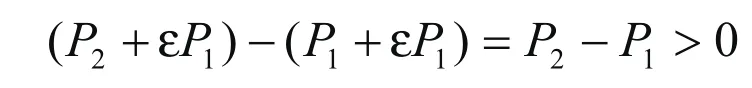
因此，L更倾向于情形（2）的结果。

在有限重复博弈下，地方政府（L）即使最终会选择策略E（在C的外力干预下），但是也会尽可能地拖延这个转化的到来，以尽可能多地获取经济收益。

（3）当C的类型为G

第一期：L选择E，两方的收益是D3，P3。

第二期：L通过第一期的结果发现了C的类型，转而选择策略G，两方的收益是εD4，εP4。

综合两期，C的总收益是D3+εD4，L的总收益是P3+εP4。

（4）当C的类型为G

第一期：L选择策略G，两方的收益是D4，P4。

第二期：L仍然选择策略G，两方的收益是εD4，εP4。

综合两期，C的总收益是D4+εD4，L的总收益是P4+εP4。

小结：对C的类型为G时两方总收益的讨论。

中央政府（C）在情形（3）和（4）中总收益的差别是：③-④=

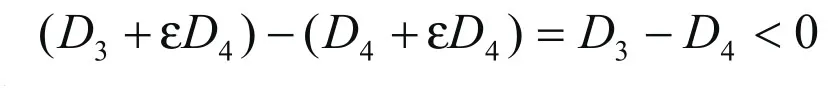
因此，C更倾向于情形（4）的结果。

地方政府（L）在情形（1）和（2）中总收益的差别是：③-④=

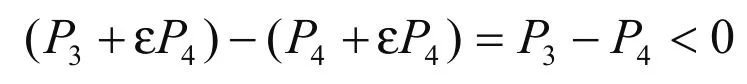
因此，L更倾向于情形（4）的结果。情形（3）成为四个解中的弱势解。

三、精炼贝叶斯均衡的判断

中央政府对地方政府策略选择判断的概率为γ(θ)、中央政府的策略规定其类型θ在行动a1上的概率σ1(a1/θ)、地方政府策略规定相对于中央政府的每一种行动a1在行动a2上的概率σ2( a2/ a1)以及地方政府对中央政府类型判断的后验概率µ(θ/a1)的数值，在不完全信息动态博弈中均使用贝叶斯法则推导。即：

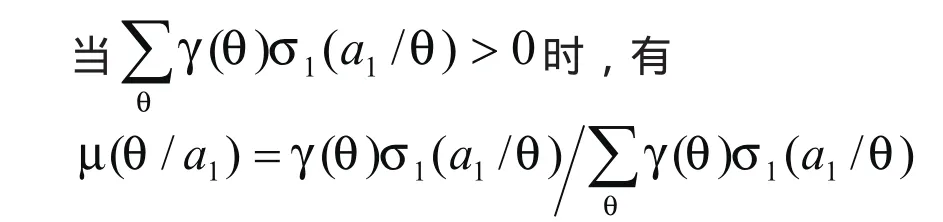
四个解均符合这个条件。

子博弈完美均衡向信号博弈的自然扩展，要求每个参与人在策略选择是必须最大化其收益，对中央政府和地方政府而言，有：

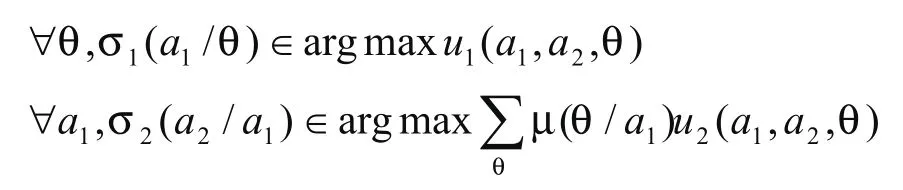
由第二部分对四个均衡中两方收益的变化，可知①、②、④均衡是精炼贝叶斯均衡，③由于其收益弱势而舍去。

四、结 论

在①、②、④3个精炼贝叶斯均衡中，均衡④是中央政府与地方政府均片面追求经济利益所达到的一种均衡，在现阶段，由于经济社会的发展，单纯以GDP为发展目标不惜牺牲其他社会利益的时代已经一去不返了，所以，以上3个均衡中，均衡④已经没有发生的现实可能性。在均衡①、②中，中央政府更倾向于均衡①，在有限重复博弈下，地方政府即使最终会选择策略E（在中央政府的外力干预下），但是也会尽可能地拖延这个转化的到来，以尽可能多地获取经济收益。所以为了达到均衡①这一最有的状态，需要一种外力促使地方政府加快由均衡②向均衡①转化的过程，这就为督查相关制度介入公益领域提供了理由。在教育、环保、土地等公益领域建立管理与监察的长效机制，并在能够通过机构和职能设置解决问题的范围内避免出现与已建立的督查相关制度相类似的问题。

以上分析以及相关条件的假设是建立在传统古典博弈理论即子博弈精炼均衡概念的基础上的，假定了参与者具有完全理性：参与者有能力推理得到其它参与者的在行动决策的理性预测以及在相应情况下自己的理性预测，因此本文博弈结果是一种理想状态下的分析。

[1] 张维迎. 博弈论与信息经济学[M]. 上海：上海人民出版社，2004

[2] 谢识予. 经济博弈论[M]，上海：复旦大学出版社，2007

[3] 朱·弗登博格，让·梯若儿. 姚洋等译. 博弈论[M]，北京：中国人民大学出版社，2002

[4] 保罗·萨缪尔森，威廉·诺德豪斯. 经济学（第十六版）[M]. 华夏出版社，麦格劳·希尔出版公司，1999

[5] 王水雄. 生育的博弈模型：中国的例子[J]. 社会学研究，2002（6）

[6] 曹国华，滕进华. 基于三方动态博弈模型的软预算约束成因及影响[J]. 重庆大学学报（自然科学版），2006，29（1）

[7] 周永务，冉翠玲. 需求信息不对称下供需双方的博弈. 系统工程与电子技术[J]，2006，28（1）

[8] 张 苏，汪传旭. 基于两阶段信号博弈的港口合作声誉模型[J]. 上海海事大学学报，2007，28（2）

[9] 肖条军，盛昭翰. 两阶段基于信号博弈的声誉模型[J]. 管理科学学报，2003，（6）

[10] 汪丁丁. 制度分析基础讲义[M]. 上海：上海人民出版社，2005

[11] 朱善利. 微观经济学[M]. 北京：北京大学出版社，2001

[12] 高鸿业. 西方经济学（微观部分）[M]. 北京：中国人民大学出版社，2000

[13] 张金马. 公共政策分析：概念、过程、方法[M]，北京：人民出版社，2004

[14] 向钢华，王永县. 一种三方不完全信息延伸威慑动态博弈模型[J]. 系统工程，2006，24（4）

The Analysis on General Signal Game Model about the Relationship Between Central and Local Governments

Luan Gui-qin Shen Ke-ying Zhuang Yi

(Business School, University of Shanghai for Science and Technology, Shanghai 200093)

The interest relationship between central and local governments is the core content of their relationship. The process of maximizing the interests for both sides is a game process. When receiving the specific signal from central government, local government estimates the attitude of central government according to the signals and guides their actions. Therefore, this article defines the relationship between central and local governments as the two-party multistage limited repeated game and chooses a classic game theory of the signaling game model to analyze the actions of central government and local government in order to seek solution of general equilibrium.

The relationship between central and local governments; Signal Game; Perfect Bayesian equilibrium