6-CRS并联机器人机构及其位置分析

车林仙 何 兵 程志红

1.中国矿业大学,徐州,221008 2.泸州职业技术学院,泸州,646005

0 引言

1965年,Stewart对Gough发明的用于轮胎检测装置的6-DOF并联机构进行了机构学意义研究,并将其应用于飞行模拟器。这种最早出现的6-SPS平台型并联机构被称为Stewart机构。1978年,Hunt[1]首次提出将Stewart机构作为机器人操作手,由此产生了并联机器人机构学这一新分支。1995年,Faugere等[2]提出一类特殊的Stewart机构。1998年,Dafaoui等[3]基于点面之间的距离约束,构造了新型广义Stewart机构。金振林等[4-5]通过改变支链的布置方式,构造了2-2-2型6-SPS和2-2-2型6-PSS正交广义Stewart机构。Gao等[6]提出由点、线、面三种几何元素通过角度约束以及距离约束来构造并联机构的新方法,并发明了许多新型广义Stewart机构。其后,甘东明等[7]、车林仙[8]也根据Gao的理论,先后提出了基于点线之间距离约束的6-CCS、6-CPS正交广义Stewart机构。本文借鉴已有研究成果,并结合单开链(single-opened-chain,SOC)理论[9],提出一种新型6-CRS广义Stewart并联机器人机构,给出其几何模型。该机构可用于并联机床、并联微动机器人、六维力/力矩传感器等领域。本文的研究可为6-CRS广义Stewart并联机器人机构的进一步研究和实用化提供理论基础。

1 6-CRS并联机器人机构结构分析

1.1 机构模型

图1所示为新型6-CRS并联机器人机构的运动简图,该机构由动平台P-E1E2E3、机座A1-A2-A3和6条支链BiCiD i(i=1,2,…,6)组成。其中,每条支链由圆柱副(C)、转动副(R)和球铰(S)组成,C副与R副的轴线互相平行。因此,支链结构为SOC{-C∥R-S-}。6条支链的结构和尺寸完全相同,连杆B iCi和CiD i的长度分别为l1和 l2。6条支链分为3对,而3对支链与动平台相连的3对S副分别分布在边长为2a的立方体(图1中简化为正三棱锥)的3个互相垂直的表面上,且各对S副中心连线在空间两两互相垂直;各对S副中心的距离为2b。每对支链的两个C副共轴线,3对C副的轴线分别位于基础六面体的3个互相垂直的表面内,且3条轴线互相垂直。

3对支链具有相同姿态,且动平台立方体与基础平台立方体的对应面分别平行时为机构初始位姿,如图1a所示。建立与动平台固结的坐标系σ：Pxyz,原点P位于动平台的几何中心,3个坐标轴分别平行于动平台立方体的3个互相垂直的棱边;建立与基座固结的坐标系∑：OXYZ,且初始位姿时,定系 ∑与动系σ重合。其余未加说明的符号及其意义见图1。

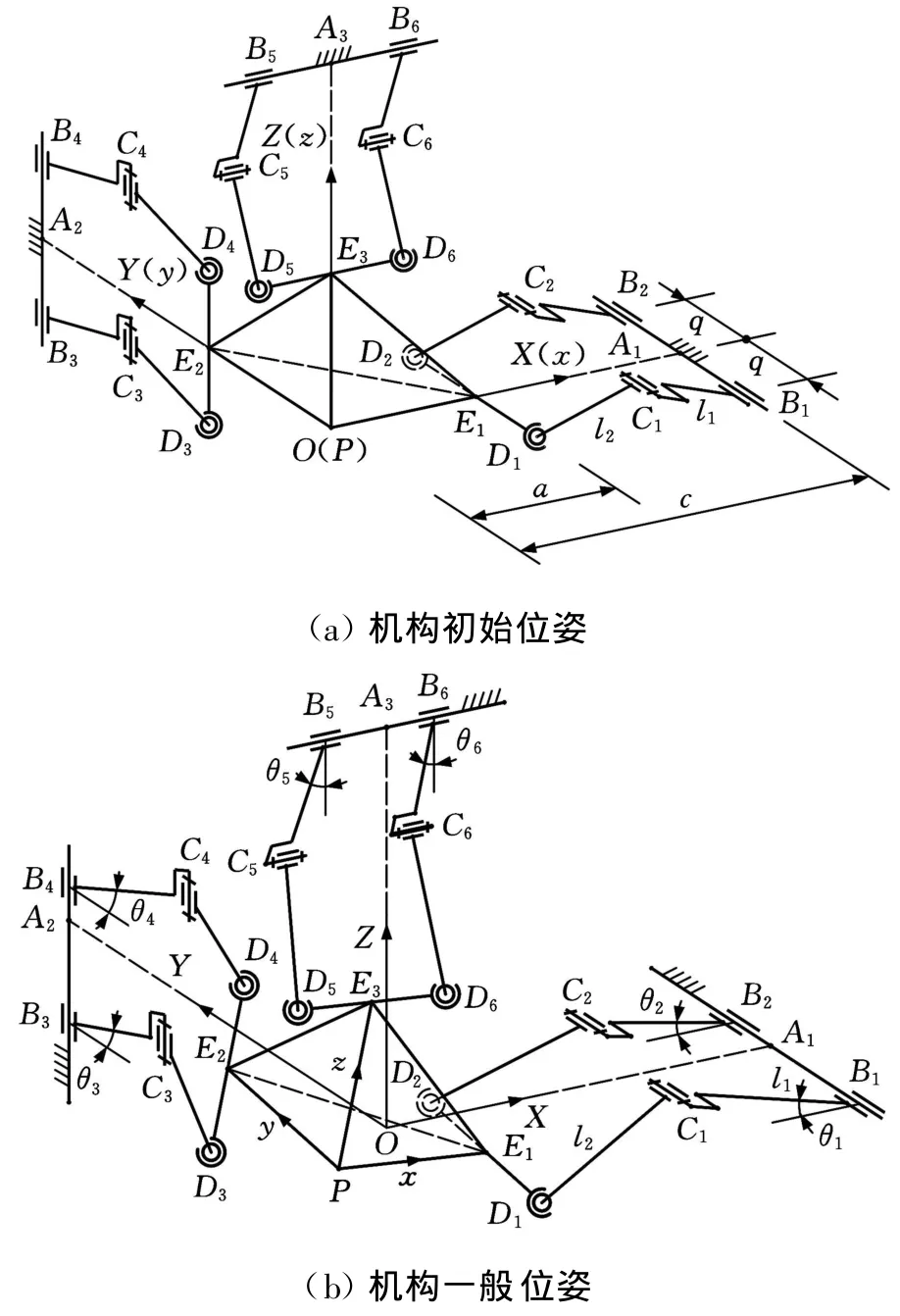
图1 新型6-CRS并联机器人机构简图

1.2 自由度分析

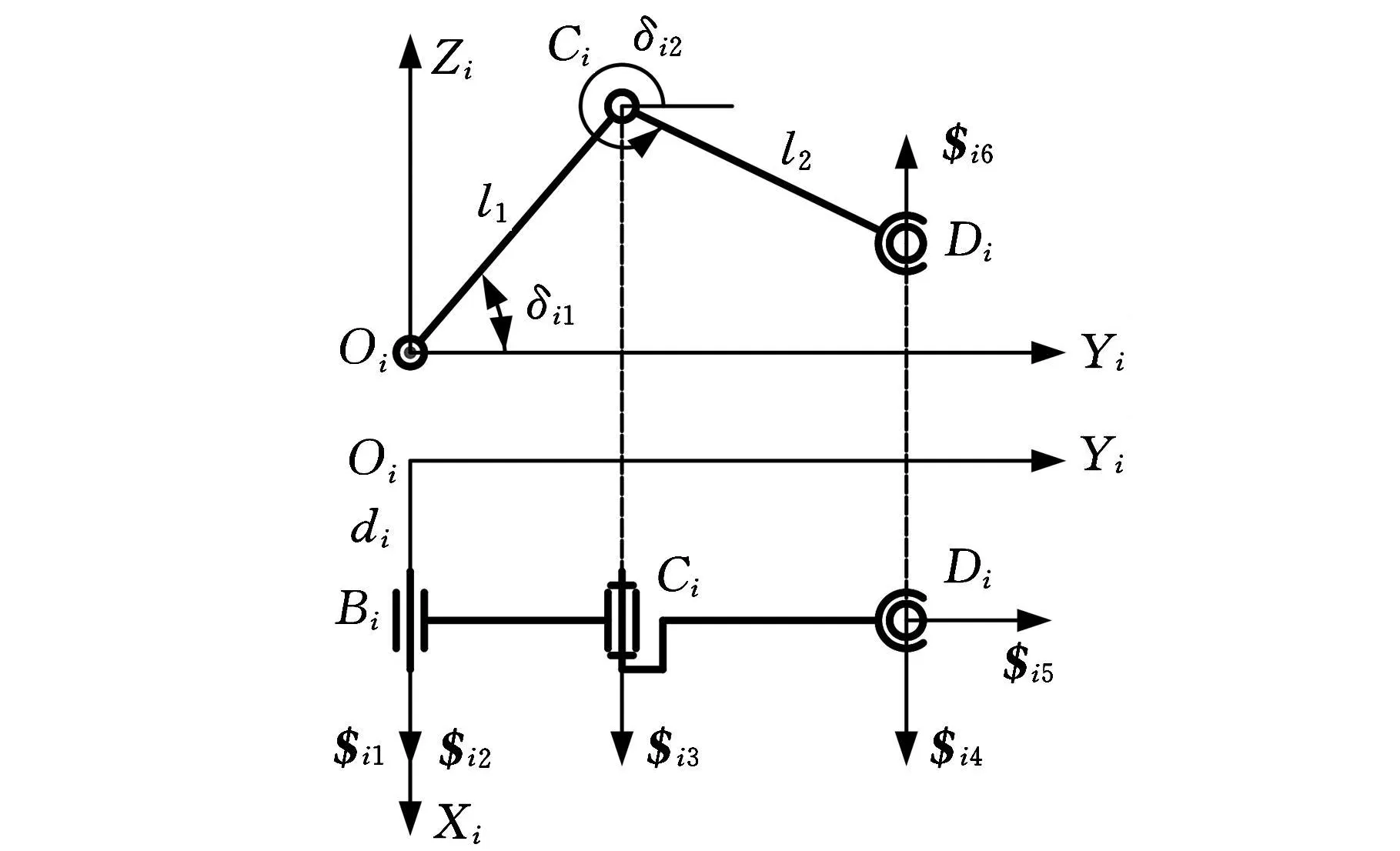
图2 6-CRS并联机器人机构的支链坐标系

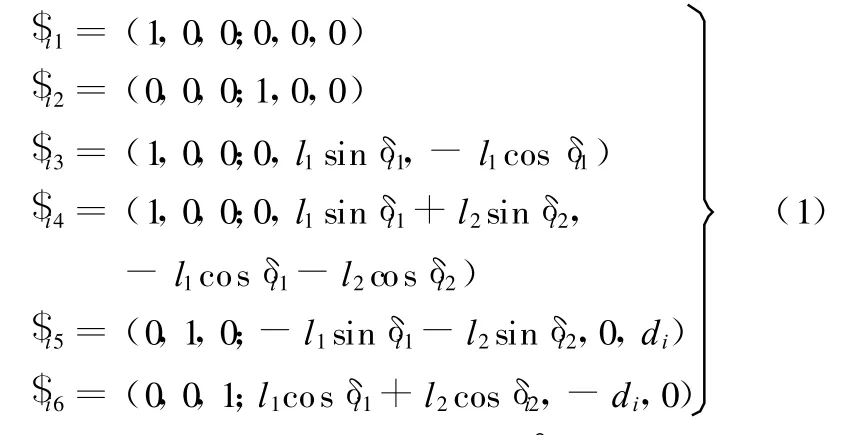
当 δi1=δi2或 δi1=δi2-180°时 ,第 i支链中BiCi与CiD i共线,运动螺旋系的秩为5,此时该支链处于奇异位形(当对该支链的C副施加转动主驱动时,动平台可连续运动,此位置为该支链的切换点;当对该支链的C副施加移动主驱动时,对动平台增加意外约束,对该支链的控制将失效。)。

运动螺旋描述的是刚体的瞬时运动,因此还需判断机构自由度的连续性。在第i支链中,动平台发生连续运动后,C副的轴线始终为X i轴,R副的轴线始终平行于X i轴。因此,第i支链运动螺旋系始终为式(1)的形式,在非奇异位形下,始终不存在反螺旋,所以,在机构的任一非奇异位形处,6条支链始终不约束动平台的自由度,即机构具有6个连续自由度。

应用黄真等[10]提出的修正 Grübler-Kutzbach公式求得机构自由度M=6,即该机构具有3个移动自由度和3个转动自由度。

1.3 输入选取

设刚化输入(即固定驱动)后第i支链运动螺旋系的反螺旋为

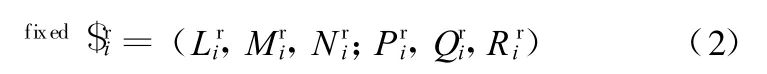
1.3.1 转动输入为主驱动

若选取各支链与定平台相连的6个C副中的转动输入(即刚化运动副＄i1)为主驱动,则由反螺旋定义[10]可得

式(3)的秩为5,其基础解系为

1.3.2 移动输入为主驱动

若选取各支链与定平台相连的6个C副中的移动输入(即刚化运动副＄i2)为主驱动,则由反螺旋定义[10]可得

(1)δi1=δi2 或 δi1=δi2-180°的情形 。当δi1=δi2 或 δi1=δi2-180°时,连杆 BiCi与CiD i的中心线共线,式(5)的秩为4,其基础解系为

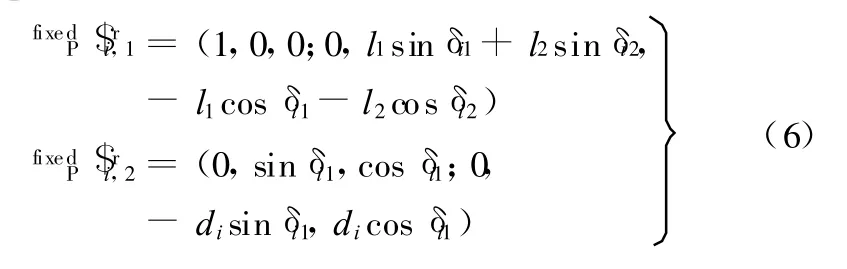
(2)δi1≠δi2且 δi1≠δi2-180°的情形 。当δi1 ≠δi2且 δi1 ≠δi2-180°时 ,式(5)的秩为 5,其基础解系为作用线过点D i且与连杆BiCi、CiD i所确定的平面垂直。刚化输入后,各支链均有1个反螺旋(亦即分别增加1个反螺旋),故支链内输入选择合理。根据机构结构特点,增加的6个反螺旋力线矢可分为 3对

2 6-CRS并联机器人机构位置分析

由图1可知,点Aj(j=1,2,3)在定系 ∑中的坐标矢量为

点B2j-1、B2j在定系∑中的坐标矢量为

式中,e1、e2、e3分别为沿Y 、Z、X 轴方向的单位矢量;d2j-1、d2j分别为Aj到B2j-1、B2j的距离(取代数量,与坐标轴正向同向时为正,反之为负)。

为防止支链B 2j-1 C2j-1与B2jC 2j的圆柱副发生干涉,圆柱副参考点B2j-1与B2j间具有距离约束

式中,Δd为根据圆柱副结构设定的距离阈值。

参考点P在定系∑中的坐标矢量为

点Di在动系σ中的坐标矢量为

式中,a为机构立方体动平台边长的1/2;b为机构立方体动平台同一表面上两球铰中心距的1/2。

当用Z-Y-Z型欧拉角(α,β,γ)描述动平台的旋转运动时,其姿态矩阵为

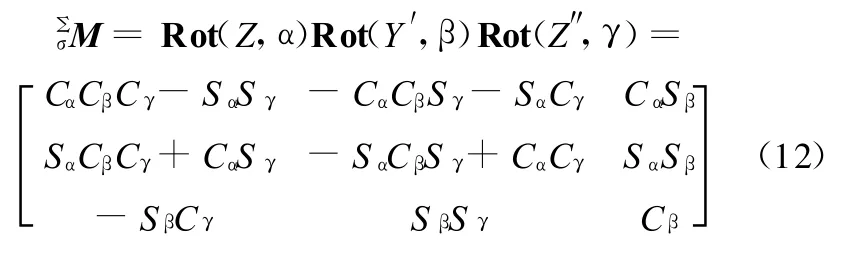
其中,Sα=sinα,Cα=cosα,其余类似。

点D i在定系∑中的坐标矢量为

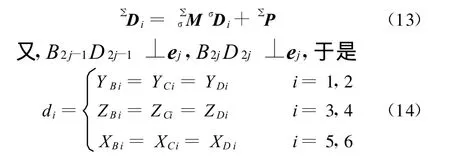
2.1 转动输入为主驱动时的位置分析

已知6个C副的转动驱动角θi,求动平台参考点P 的坐标(XP,YP,ZP)及欧拉角(α,β,γ)即为位置正解。

点Ci在定系∑中的坐标矢量为

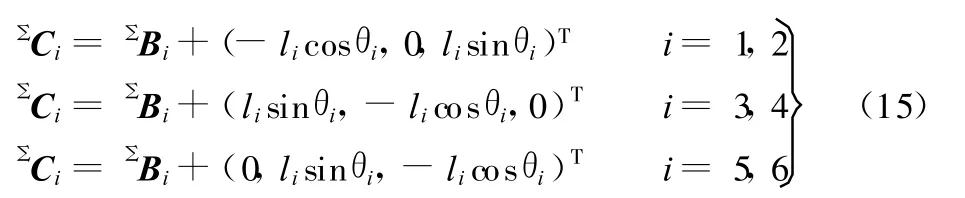
根据杆长约束条件有

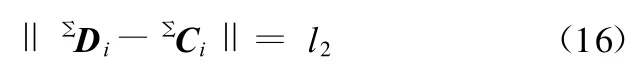
将式(13)、式(15)代入式(16),并注意到式(14),得

式(17)～式(19)即为转动输入为主驱动时的位置正解方程组。因该组方程为强耦合非线性方程组,故其求解较困难,本文应用自适应逃逸差分进化算法求解。待求出位置正解后,将之代入式(13),并结合式(14),可求出6个C副的直线位移d i。

已知动平台参考点P的坐标(XP,YP,ZP)及欧拉角(α,β,γ),求 6个 C 副转动驱动角 θi即为并联机构的位置反解。将式(17)～式(19)整理为

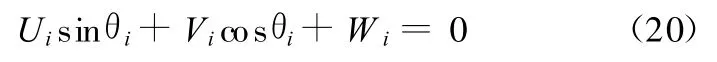
式中,Ui、Vi、Wi可由机构结构参数和动平台位姿参数表示出(限于篇幅,此处略去其详细表达式)。

由式(20)解得

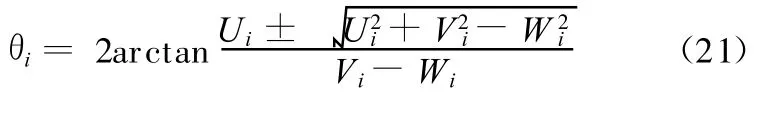
式(21)即为机构的位置反解,共有 64组反解。

2.2 移动输入为主驱动时的位置分析

已知6个C副的直线驱动位移d i,求动平台参考点 P 的坐标(XP,YP,ZP)及欧拉角(α,β,γ)即为位置正解。

联立式(13)、式(14),得

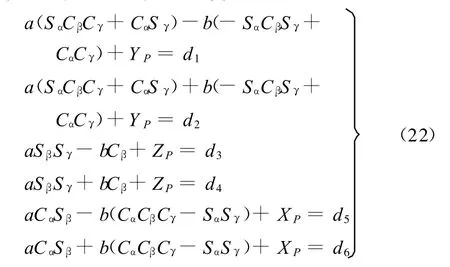
将式(22)整理为

其中,0＜ d/(2b)≤τj≤1,j=1,2,3。

(1)τ2=1的情形。若 τ2=1,则 β =0,动平台的姿态角为绕Z轴的旋转角,即为α+γ(此时必须有τ1=τ3,否则无解)。可由式(23)解得 α+γ=arccosτ1。

(2)τ2≠1的情形。由式(23)解得

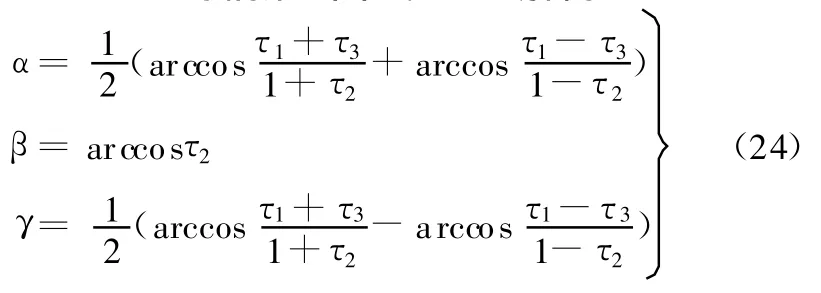
将式(24)代入式(22),很容易求得动平台参考点P的坐标(XP,YP,ZP)。

已知动平台参考点P的坐标(XP,YP,ZP)及欧拉角(α,β,γ)时,由式(22)求出6个C副移动驱动位移di即为位置反解。以移动输入为主驱动时,该机构仅有1组位置反解。

3 转动输入为主驱动时位置正解的自适应逃逸差分进化算法

差分进化算法(differential evolution,DE)是Storn等[11]于1995年提出的一种新型进化算法,作为一种性能卓越的优化工具,已被应用于机构优化综合[12]及并联机构位置正解的求解[13]等领域,取得了较好结果。为改进基本 DE(simple DE,SDE)的寻优效率,提出一种基于混沌的自适应逃逸差分进化算法(adaptive escape differential evolution,AEDE)。

3.1 AEDE算法

不失一般性,本文仅考虑全局最小化问题

其中,Φ(x)为目标函数,Ω为解空间(约束域),x=(x1,x2,…,xK)T∈ Ω为优化变量,K为优化变量的维数。优化变量x的上、下界约束向量分别

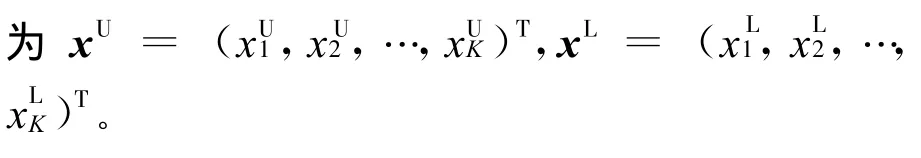
DE的控制参数为种群规模N pop、缩放因子F及交叉因子 Pcro。记进化至第 t代的种群为对应于式(25)的优化变量,以目标函数Φ(x)作为适应度函数;直至第t代的全局最优个体为不同SDE的区别在于采取不同的差分策略实现变异操作,常见策略有[11]：DE/rand/1/bin 、DE/rand-to-best/1/bin 、DE/best/2/bin(依次简记为 DER1、DERB1、DEB2)。对于并联机构位置正解问题,采用DEB2策略的SDE性能最好,因此本文的AEDE按DEB2策略进行变异。首先给出种群陷入局部最优区域的判据,再描述AEDE的基本步骤。

大量实验表明,当x best连续Δt代未更新(通常取Δt=15～20),种群多样性迅速降低,个体明显趋同。若仍按原来的策略进化,群体已很难逃离xbest的邻域,出现早熟收敛。

定义2 当x best未达到预设精度且连续Δt代未更新,则认为种群陷入局部最优区域。

AEDE的基本思想是：当种群陷入局部最优区域时,用混沌方法生成若干新个体取代xbest邻域内的个体,并将{xbest,Φ(xbest)}的信息清空后再重置,使群体逃离局部最优区域继续寻找全局最优解。为防止最优信息丢失,另设记忆单元{mbest,Φ(mbest)}记录目前搜索到的最优个体。即每次更新x best后,都将 Φ(x best)与 Φ(m best)比较,若 Φ(xbest)更小,则用{xbest,Φ(xbest)}取代{mbest,Φ(m best)}。

由于Kent映射生成的混沌序列分布均匀,具有良好的遍历性[14],因此本文将其引入群体逃逸操作。Kent映射的表达式为[14]

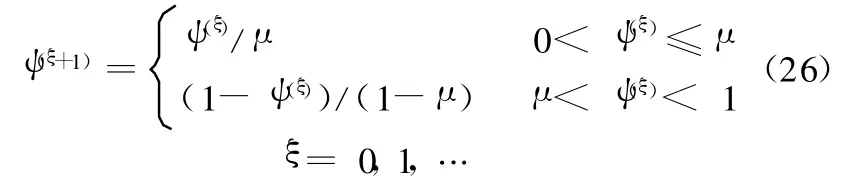
式中,常数μ∈(0,1),且μ≠0.5,本文取μ=0.4;

根据具体问题设置邻域半径σneigh,若

则用基于Kent映射式(26)的混沌算子生成新个体取代 xn′。

AEDE是将群体逃逸操作自适应嵌入SDE形成的一种混合算法,其基本流程如下。

(1)初始化。设置控制参数 N pop、F、P cro、T(最大进化代数)、Δt、εpop、σneigh、t=0;初始化种群并评价每个个体。其中,rand()为(0,1)范围内均匀分布的随机数。

(3)终止检验。如果满足终止准则,则输出结果并停止;否则,执行(4)。

(4)群体逃逸。若全局最优个体xbest连续Δt代未更新,则在(0,1)范围内随机生成K维初始向量,然后按式(26)迭代生成混沌向量序列(若干新个体),再依次用这些新个体取代x best邻域内的个体。并将 xbest及其适应度等信息清空后再重置。

3.2 基于AEDE的机构位置正解

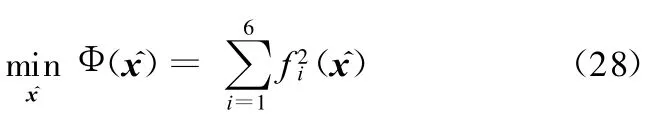
求解时,对寻优变量进行归一化处理,使所有变量均在[0,1]范围内寻优,即将寻优变量 xi按下式映射至实际取值区间,再应用式(28)计算个体的适应度：

4 6-CRS并联机器人机构位置正解实例

已知机构尺度参数：l1=80mm,l2=120mm,a=35mm,b=25mm,c=190mm,Δd=30mm。以6个C副中的转动输入为主驱动,各驱动角求机构位置正解 。

应用AEDE求机构位置正解的控制参数：N pop=30,T=500,F=0.5,P cro=0.9,Δt=时,本文认为xbest在第t+1代未更新。设置待求变量的实际取值范围：XP,YP,ZP∈[-2c,2c],α,β,γ∈ [-π,π],可接受误差εaccept=10-10。独立运行AEDE 200次(全部收敛),得到16组不同位置正解(表1),达到可接受误差的平均进化代数为199.2代。

文献[13]应用DER1求Stewart机构位置正解的控制参数为：N pop=200,T=1 500,εaccept=10-4,达到可接受误差的平均进化代数为548.4代。与文献[13]相比,本文方法计算量更小、速度更快、精度更高。

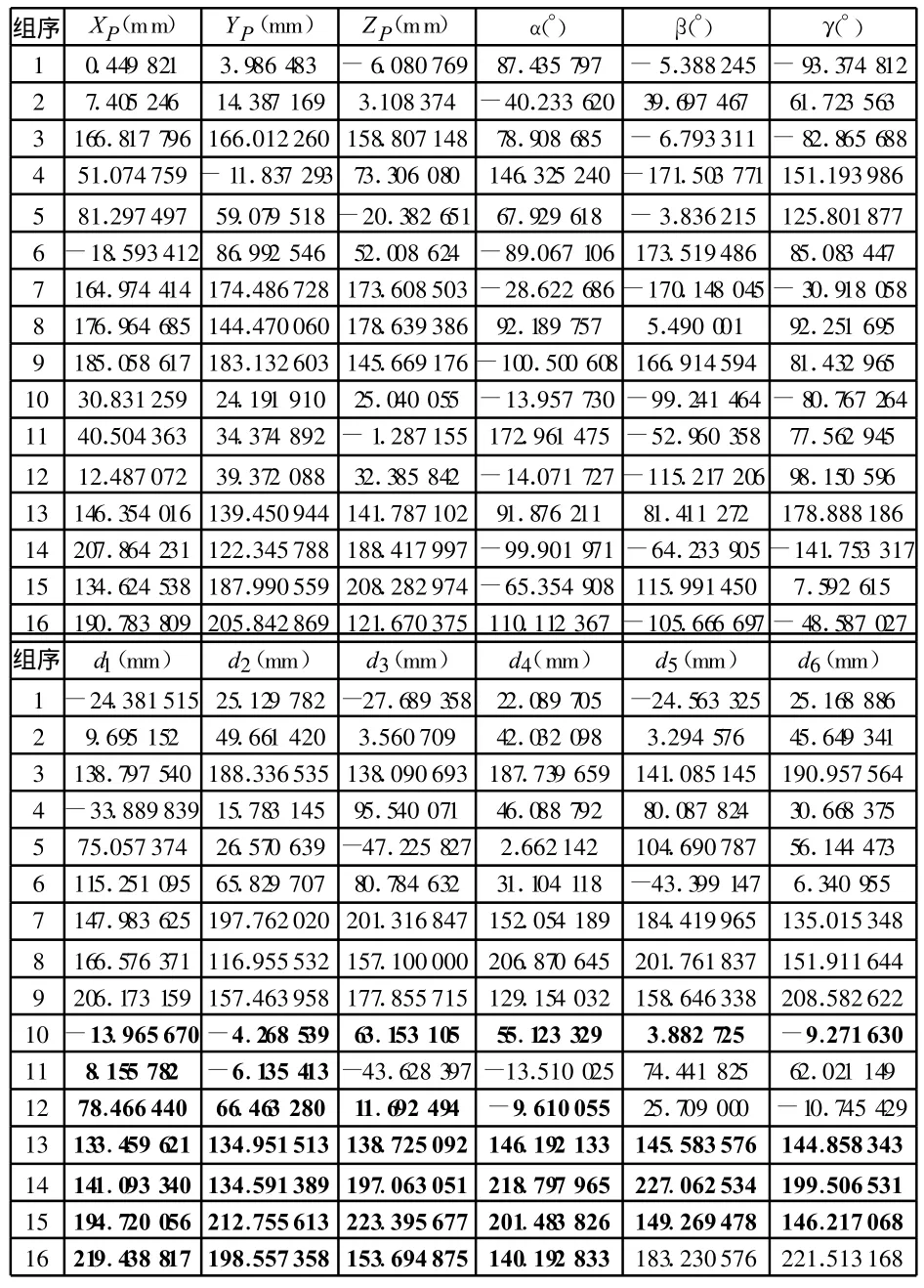
表1 实例的16组实数位置正解

由式(9)可知,第10～16组解的支链间会发生圆柱副干涉(表1粗体数据),应舍弃;其余各组解支链间不发生干涉,但由初始位姿只能到达第1～3组解确定的位姿。

对所有正解进行验证,即应用式(21)求反解。反解结果中正好有1组与驱动输入吻合,表明本文方法是正确的。

为了评价AEDE在并联机构位置正解中的计算性能,将该算法与 3种 SDE(分别采用DER1、DERB1、DEB2 变异策略)、粒子群算法(particle swarm optimization,PSO)进行了对比测试。实验环境：Intel CoreTM2-1.66GHz CPU,2GB RAM,WinXP OS,MATLAB6.5编程。5种算法的可接受误差均为 εaccept=10-10。SDE中,除 DETR1的 Pcro=0.6外,其余参数与AEDE相同;PSO与DE类似,仍在[0,1]范围内寻优,N pop=30,T=500,惯性权重w线性递减,w max=1.2,w min=0.1,粒子最大飞行速度v max=0.3,加速度常数C1=C2=1.8。5种算法的种群规模、最大进化代数均相同,因此适应度函数的评价次数相同,耗时基本相当。表2给出了5种算法对于位置正解问题50次随机独立计算的统计结果,最优指标加粗显示。5种算法50次随机独立计算的最优目标函数平均值进化曲线如图3所示。

表2 位置正解中5种算法的统计结果比较

图3 位置正解中5种算法的进化曲线比较

从上面的计算结果可以看出,AEDE除最优目标值与DEB2同为最好、平均耗时略长外,其余指标均优于其他4种算法。笔者还测试了其他驱动角条件下的位置正解问题,统计结果与表2接近。由此可知,AEDE在克服早熟收敛、计算精度和鲁棒性等方面均具有明显优势。

5 结论

(1)提出了一种新型6-CRS广义Stewart并联机器人机构,并应用螺旋理论分别分析了以C副中的转动和线性移动作为主动输入的合理性。分别建立了以转动和移动输入为主驱动时的机构位置正解非线性方程组,并推导了以移动输入为主驱动时的位置正解封闭表达式。

(2)将混沌逃逸算子融入SDE形成混合差分进化算法——AEDE,并应用该混合算法求以转动输入为主驱动时的机构位置正解非线性方程组。测试结果表明AEDE在成功率、计算精度等方面均明显高于PSO、SDE算法。

(3)利用数值方法对机构的位置正反解进行了验证：根据已知转动输入求出机构的所有位置正解;再分别以每组位置正解作为已知动平台位姿,反解出相应的转动输入,其中一组位置反解与已知转动输入相同。证明该正解的求解过程是正确的。

[1] Hunt K H.Kinematic Geometry of Mechanisms[M].London：Oxford University Press,1978.

[2] Faugere JC,Lazard D.Combinatorial Classes of Parallel Manipulators[J].Mechanism and Machine Theory,1995,30(6)：765-776.

[3] Dafaoui E M,Amirat Y,Pontnau F,et al.Analysis and Design of a Six-DOF Parallel Manipulator：Modeling,Singular Configurations and Workspace[J].IEEE Transactions on Robotics and Automation,1998,14(1)：78-91.

[4] 金振林,高峰.一种新颖的6自由度并联机床结构型式及其局部各向同性分析[J].中国机械工程,2001,12(12)：1359-1361.

[5] 金振林,王军,高峰.新型6-PSS并联机器人工作空间分析[J].中国机械工程,2002,13(13)：1088-1090.

[6] Gao X S,Lei D L,Liao Q Z,et al.Generalized Stewart-Gough Platforms and Their Direct Kinematics[J].IEEE Transactions on Robotics,2005,21(2)：141-151.

[7] 甘东明,廖启征,王品,等.新型6-CCS并联机器人机构的运动学正解及仿真[J].中国机械工程,2007,18(24)：2903-2906.

[8] 车林仙.6-CPS正交并联机器人位置正解分析[J].农业机械学报,2009,40(11)：212-218.

[9] Shen H P,Yang T L,Ma L Z.Synthesis and Structure Analysis of Kinematic Structures of 6-dof Parallel Robotic Mechanisms[J].Mechanism and Machine Theory,2005,40(10)：1164-1180.

[10] 黄真,赵永生,赵铁石.高等空间机构学[M].北京：高等教育出版社,2006.

[11] Storn R,Price K.Differential Evolution-a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,11(4)：341-359.

[12] Acharyya SK,Mandal M.Performance of EAs for Four-bar Linkage Synthesis[J].Mechanism and Machine Theory,2009,44(9)：1784-1794.

[13] 王雪松,郝名林,程玉虎,等.基于差分进化的并联机器人位姿正解[J].中国矿业大学学报,2008,37(5)：664-669.

[14] Xiang T,Liao X F,Wong K W.An Improved Particle Swarm Optimization Algorithm Combined with Piecewise Linear Chaotic Map[J].Applied Mathematics and Computation,2007,190(2)：1637-1645.