基于有限元法的楔环参数概率约束优化
2010-05-31杜宏伟羊海涛
杜宏伟 姚 进 羊海涛
1.四川大学,成都,610065 2.中国工程物理研究院总体工程研究所,绵阳,621900
0 引言
在一般的有限元结构分析中,有限元问题的所有参数是确定不变的,如几何尺寸及拓扑形状、材料属性及载荷等,计算结果也是确定的。在实际产品中这些参数均由于制造和测量误差、使用环境而具有随机性,因此载荷对产品作用的实际结果也具有随机性。利用有限元概率分析,将每个输入参数视为服从一定分布的随机变量,通过大量采样点模拟其分布并进行数值分析,获得系列解,进而计算输出变量的分布及可靠度。在有限元概率分析的基础上开展可靠性优化设计,目的之一是在产品工作可靠度不低于规定水平的条件下,其性能达到最佳。由于设计变量和参数具有随机性,约束中含有概率约束,可靠性优化设计模型比确定性优化模型的求解困难得多。可靠性优化模型按优化目标的不同可分为均值E模型、方差V模型、概率P模型、混合模型等。其中最有代表性且最常用的是E模型,这时的目标函数可以表示尺寸、质量、成本或某项性能指标[1]。
楔环是近年来发展的用于圆筒连接的一种新型结构,该结构连接紧凑、表面平顺、拆卸方便,因而具有优良的流体动力学性能及维修性能,在鱼雷部件连接中得以应用。随着整体厚度的减小,局部应力及变形对结构参数及材料性能更为敏感,楔环结构强度及刚度降低,工作可靠性随之下降。卜广志等[2]、毛昭勇等[3]利用楔环最大应力解析式,视强度与应力为正态分布的随机变量,在强度可靠度约束下对楔环结构进行优化,减小其厚度及体积;黄鹏等[4]采用有限元接触分析及一阶方法对楔环结构进行优化,降低了应力水平。前者的解析方法未考虑复杂的接触问题,后者的有限元分析未考虑结构变量及状态变量的随机性。
本文利用有限元法对楔环在配合尺寸、材料性能偏差、载荷等不同条件下的强度、刚度进行接触仿真分析,采用响应面中心组合(centrl composite)设计抽样并拟合输出变量的响应面,获得在设计参数范围内的二次多项式。在研究考虑概率约束的优化问题时,以得到的简化模型为基础,采用一次二阶矩方法将随机约束等价转换为确定型约束,然后求解确定性的优化问题,获得满足概率约束条件下的楔环厚度优化结果。
1 概率优化方法
本文的目的是在概率约束条件下对设计随机参数均值进行优化,因此选择概率优化模型为均值E模型。对这种模型的求解,就是在概率可行域内寻找E{f(X)}最小值时的设计点X*,即是概率优化设计问题的最优解,其优化模型如下:

式中,X为随机设计变量和随机参数(如材料性能)组成的向量;f(X)为目标函数;gu(X)为受概率约束的函数;hu(X)为一般约束函数。
为便于优化计算,采用一次二阶矩法[5-6]将随机约束等价转换为确定型约束。
将gu(X)在均值处以泰勒级数展开,并取其线性项:
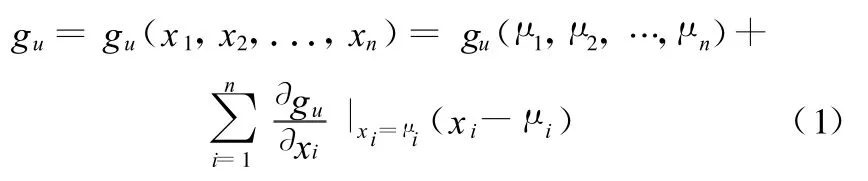
则gu(X)的均值及标准差分别为

假设随机约束函数gu(X)服从正态分布,则由随机约束P{gu(X)≥0}≥au可得

即
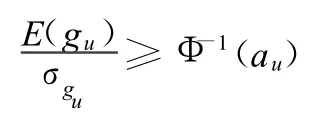
则

若随机约束为P{gu(X)≤0}≥au,则

2 分析模型
2.1 几何模型
图1所示为楔环结构轴对称几何模型,同时该结构具有上下对称形式。楔环结构主要由三部分组成:A、B件分别为开环槽的被连接圆筒;C件为用于连接圆筒的环带,由两条楔状环带组合而成。两条楔状环带通过外筒B表面局部U形孔穿入圆筒组合槽中并楔紧。装配完成后环带C上边右段与圆筒B接触,下边左段与圆筒A接触。在受轴向拉伸载荷作用下,A、B圆筒有脱开趋势,通过环带C上下两边分别与A、B接触连接,此时环带C处于挤压状态。由于圆筒变形及环带滑移,环带C左右边均可能与圆筒接触,因此总计设置4对接触,如图1a右视图所示。

图1 楔环模型及结构变量
2.2 有限元模型
在轴向拉伸载荷下,楔环结构中A、B件的结构与受力具有一定相似性,楔环结构参数缩减为4个(x1、x2、x3、x4),见图 1b。根据ANSYS 软件中APDL参数化设计语言编制概率分析程序[7],建立有限元参数化模型。4个结构变量与材料屈服强度x5、轴向拉伸载荷 x6均为服从GAUSS(正态)分布的输入变量,见表1。为考察楔环连接结构强度及刚度,确定输出变量为强度与应力之差SS(强度为材料屈服强度,应力为最大von Mises等效应力)、最大横向(径向)位移UX。

表1 输入变量及分布
材料为 45钢,根据双线性随动强化材料(BK IN)设置参数,模拟材料塑性行为、PLANE82轴对称单元。为避免结构参数变化后网格密度差异对应力结果的影响,不采用自适应网格,通过线段单元份数控制网格尺寸,高应力区网格加密。根据装配接触部位及受力后可能的变形接触,按图1a右视图设置4对面-面接触。接触对设置参数法向刚度因子FKN=1,渗透容差因子FTOLN=0.1,摩擦因数MU=0.1。采用Augment Lagrange算法处理接触、Full Newton Raphson法求解,计算时采用自动时间步长和线性搜索以保证求解效率和稳定性[4]。
有限元概率分析过程如下:首先根据设计变量初值对参数化有限元模型进行分析,提取输出变量 SS及 UX,生成 APDL命令流文件 *.PDAN;然后初始化程序并重新读入 APDL文件,进入Prob Design进行随机输入输出变量设置、计算方法选择、计算分析并处理结果。
3 计算分析
3.1 初始概率分析
采用 Monte Carlo计算方法中拉丁超立方(Latin Hypercube)方法抽样100次,按表1所列参数值进行有限元概率分析,检查变量 x1样本,图2表明其符合GAUSS分布,均值及标准差与表1要求相当,样本抽样数足够;其余样本检查同此。计算输出结果见表2,满足可靠度要求并有一定的优化空间。输出灵敏度图见图3,在表1变量标准差确定的初始设计区间,对SS影响显著的结构参数为x1,为正相关;对UX影响显著的结构参数为x 3、x1、x4,其中 x3、x1为负相关,x4为正相关。在减小楔环厚度时,由于 x3、x4减小将增大UX(因x3影响大于x4影响),可以通过增大x1进行补偿。

图2 x1样本分布及均值
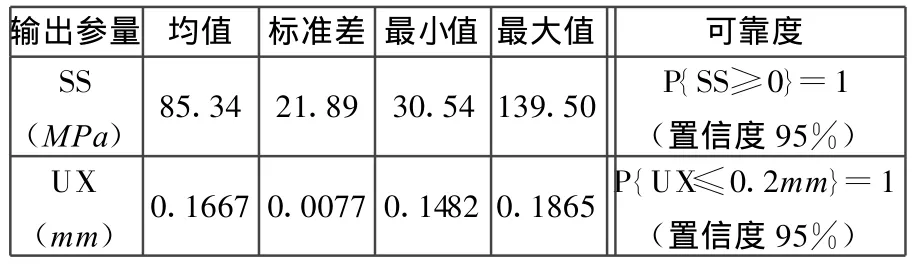
表2 初始概率分析结果
3.2 概率优化设计
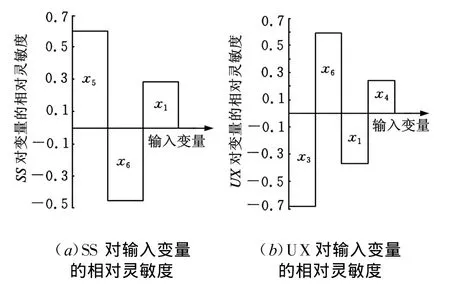
图3 SS及UX对输入变量相对灵敏度直方图
以随机变量X=(x1,x2,x3,x4,x 5,x6)为输入参数,其中包括4个设计变量均值和2个状态变量均值;优化目标为楔形环厚度。根据强度及刚度的可靠度要求,楔环结构屈服强度大于等于最大von Mises等效应力的概率不小于0.95,楔环结构最大横向(径向)位移小于等于0.2mm的概率不小于 0.95,由正态分布函数表查得

采用响应面中心组合(centrl composite)设计抽样计算,6个随机变量,循环计算出45个样本点。运用向前分步回归方法拟合输出变量SS及UX的响应面,略去不显著项,获得在设计参数范围内的二次多项式如下:

式中,x1,x2,x3,x4的取值均为以毫米为单位的数值;x5、x6的取值分别为以兆帕、牛为单位的数值。
根据式(2)~式(5)将随机约束等价转换为确定型约束,其中屈服强度x5、轴向力x6的均值及标准差在优化求解中考虑为常量,优化后设计参数均值为(10mm,9.25mm,1.81mm,1mm,450MPa,90000N),调整后见表3,楔环总厚度从10mm减小为6mm。根据表3优化参数进行有限元概率分析验算的结果见表4,满足优化约束条件。从表 2、表 4 对比可以看出,优化后 x1、x 2、x3、x4参数变化对UX影响不大,主要原因是 x1、x2、x4引起的变化对x3引起的变化有相互抵消的趋势,因此在优化过程中主要是SS的约束在起作用。
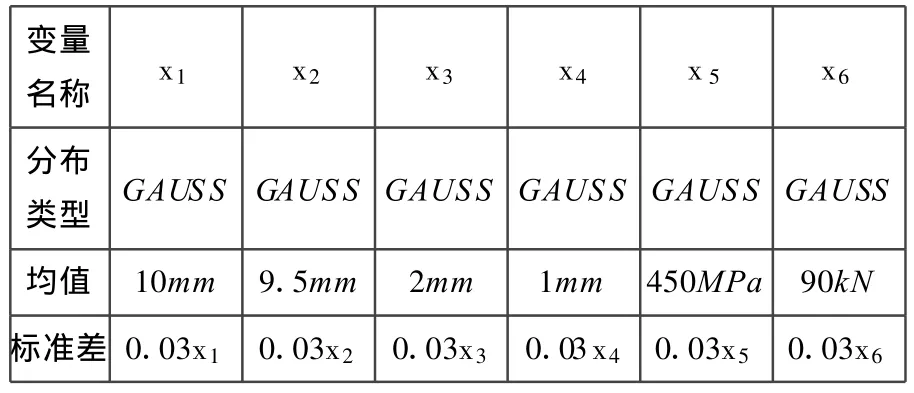
表3 优化后输入变量及分布
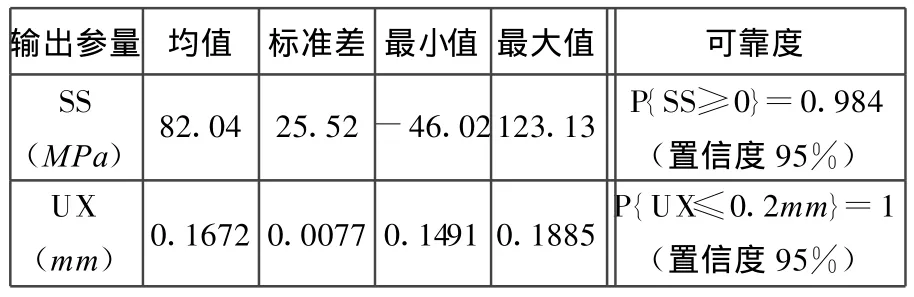
表4 优化后概率分析结果
4 结论及讨论
本文综合利用有限元概率分析、响应面设计、概率约束优化设计对楔环结构进行优化,在满足楔环强度、刚度可靠度要求的条件下减小楔环厚度,使得楔环连接更加紧凑。本文方法在具体应用中应注意:
(1)有限元接触分析的应力结果受计算参数设置、网格划分影响较大,需要反复选择并进行调试,使计算易于收敛,结果合理。
(2)要以响应面精度保证约束精度,这需要选择具有代表性的样本及合适的拟合方法,准确描述极限状态曲面的概率特征。本文采用中心组合抽样及最小二乘法拟合,SS响应面标准差约为9.2MPa,UX响应面标准差约为0.0022mm,不超过仿真最小应力及位移的3%,拟合精度满足分析要求。更高精度的响应面拟合可采用高阶拟合或神经网络,但高阶拟合计算量大,神经网络不能显式表达,需要处理与优化计算的衔接问题。
(3)当输出变量不为正态分布时,可以采用设计验算点法中的R-F方法,反复迭代进行概率约束优化计算。
[1] 刘善维.机械零件的可靠性优化设计[M].北京:中国科学技术出版社,1993.
[2] 卜广志,宋保维,张宇文,等.楔环连接的可靠性优化设计[J].机械科学与技术,2000,19(1):57-59.
[3] 毛昭勇,宋保维,胡海豹,等.基于可靠性的楔环连接模糊优化设计[J].机械科学与技术,2004,23(9):1019-1021.
[4] 黄鹏,莫军,徐兵.楔环连接结构参数化有限元优化设计[J].机械强度,2005,27(2):191-195.
[5] 张建国,苏多,刘英卫.机械产品可靠性分析与优化[M].北京:电子工业出版社,2008.
[6] 朱文予.机械概率设计与模糊设计[M].北京:高等教育出版社,2001.
[7] 博弈创作室.ANSYS9.0经典产品高级分析技术与实例详解[M].北京:中国水利水电出版社,2005.
