变胞机构的构态变换矩阵与运动副方位变胞
2010-05-31李树军戴建生
李树军 戴建生
1.东北大学,沈阳,110004 2.伦敦大学国王学院,London,WC2R 2LS
0 引言
变胞机构[1]自1998年首次提出后,就引起了国内外机构学研究者的关注及研究兴趣。Dai等[2]探讨了变胞机构的构态变换问题。Carroll等[3]提出了微变胞机构的概念,并应用变胞原理对空间机构加工机理进行了改革,首次提出了微机构加工的新方法。Liu等[4]研究了变胞机构的变胞方式,提出了利用杆件连接关系的变化和运动副的特性变化来实现变胞。戴建生等[5]对变胞机构的构态变换、变胞原理和变胞机构综合问题也进行了深入的研究,使得变胞机构的基础理论不断得到丰富和发展。
变胞机构的本源是变拓扑,变胞机构的构态变换主要通过结构拓扑矩阵来完成。通常变胞机构的变拓扑结构采用邻接矩阵及关联矩阵表示,并可进行矩阵运算[6-7]。文献[8-9]在此基础上将运动副符号引入邻接矩阵并加以改变,以适应运动副变化的需要,但矩阵中也没有运动副方位信息。李树军等[10]提出了一种运动链的拓扑特性矩阵,用来描述运动链的环路布局关系,用于运动链同构体的辨识;文献[11]中给出了一种空间运动链的描述和同构体辨识方法,取得了较好的辨识效果。但在文献[10-11]的对运动链的描述中没有运动副的方位特征,也缺少环路间链接关系方面的信息。文献[12]提出尺度型的概念,对机器人机构的运动轴线方位的5种特殊配置类型:平行、重合、垂直、共点、共面及其组合进行了描述,这一理念为描述机构拓扑结构提供了有价值的参考。在此基础上,文献[13]提出了一种基于环路布局的运动链的拓扑描述,此种拓扑结构虽有运动副方位特征信息,但对于研究以运动副或构件变化为主的变胞机构的构态变换尚欠便捷性。
目前所研究的变胞机构多是基于变胞机构具有可变自由度和可变构件数目的新型机构。然而,机构构态的变化还与运动副轴线方位的配置有关,即不改变运动链的自由度和拓扑元素(构件、运动副)数目,仅通过变换运动副的轴线方位配置,也可实现机构的运动空间由平面至空间(平面机构变换为空间机构)或反之的转换,称之为运动副方位变胞,对此目前还没有系统的研究。本文首先构建了一种结构拓扑信息更为丰富的构态变换矩阵,用于变胞机构的构态演化描述,然后应用该矩阵对运动副方位变胞原理和方法进行研究,进一步丰富变胞机构的设计与综合理论。
1 变胞机构的结构拓扑描述
针对变胞机构构态变换的特点,特别是针对运动副轴线方位变胞,本文首先构造出一种描述运动链连接状况、运动副类型和运动副方位特征的构态变换矩阵,用于变胞机构的构态变换。
1.1 变胞机构的构态变换矩阵
变胞机构的结构拓扑特征信息可用构态变换矩阵A来描述:

式中,Li为顺序号为i的构件;Jij为连接构件i、j的运动副。
设定:

式(1)中的aij,当j=i+1时,为2副构件Li上2个运动副轴线的相对方位;当L n为2副构件时,ain为Ln上2个运动副轴线的相对方位;其余元素为描述多副构件上连接构件Li和L j的边上的2个运动副轴线的相对方位;设p值即为同一构件两运动副回转轴线或移动平面的法线的相对方位,其约定如表1所示。

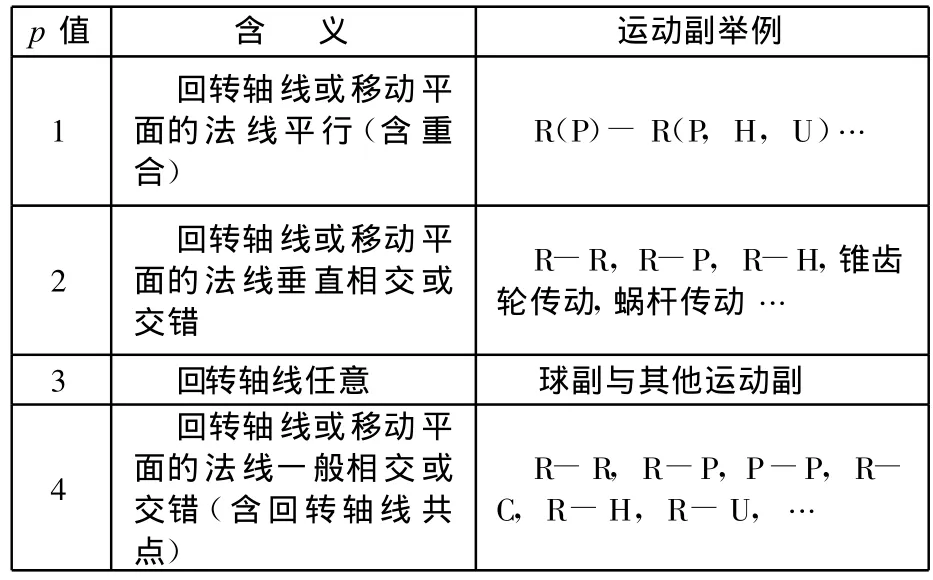
表1 同一构件两运动副回转轴线或移动平面的法线相对方位约定
1.2 构态变换矩阵的性质
根据变胞机构的构态变换矩阵的定义(式1),可知此矩阵具有下述特性:①Li所在的对角线各元素描述了顺序连接的n个构件,矩阵的行数等于构件数;②矩阵中上三角元素Jij描述了连接构件i、j的运动副的类型和连接关系;③矩阵中的下三角元素aij描述了构件各边所在的2个运动副的轴线方位,ai,i+1和ain为2副构件上2个运动副的轴线方位,其他为多副构件对应边上的2个运动副的轴线方位;④aij为构件的固有信息,为不变量,变化aij可导致运动链拓扑结构的转化;⑤既可描述平面多环运动链,也可描述空间多环运动链,并可计算运动链的自由度和构造机构的运动简图。
2 构态变换矩阵的构造举例
2.1 平面单环机构的构态变换矩阵构造
(1)二自由度4RP平面五杆机构(图1)。根据式(1)~式(3),可构造出其构态变换矩阵为
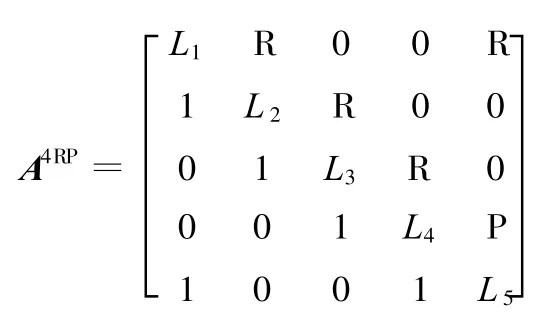
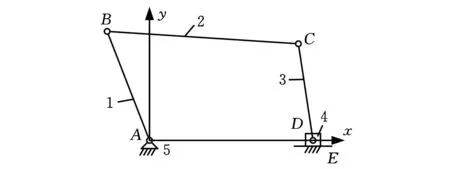
图1 4RP五杆机构运动简图
(2)具有消极自由度的平面四杆机构(图2)。根据式(1)~式(3),可构造出其构态变换矩阵为
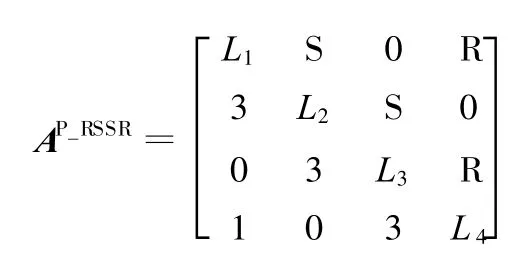
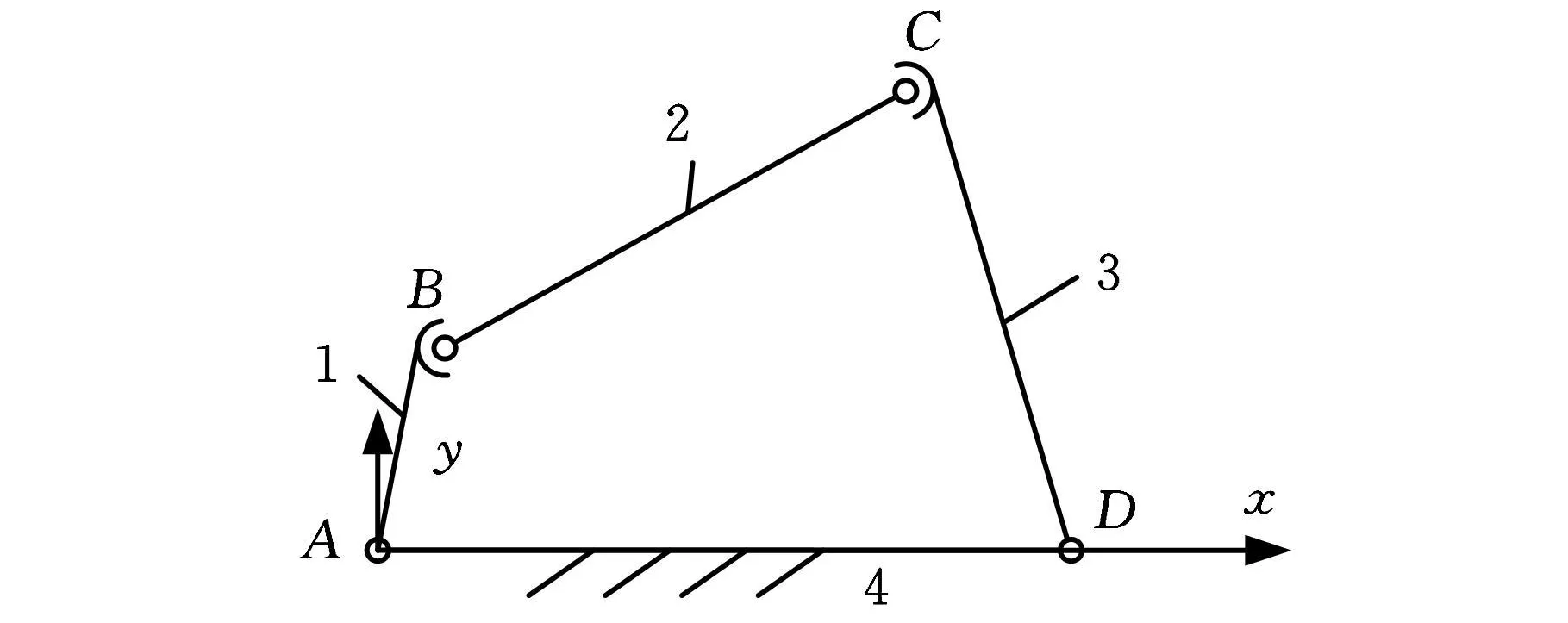
图2 平面RSSR四杆机构的运动简图
根据表1,a14=1表示构件4上的2个运动副A、D轴线平行,故该机构退化为平面四杆机构。
2.2 平面多环机构的构态变换矩阵构造
(1)平面3-RRR并联机构(图3)。根据式(1)~式(3),可构造出其构态变换矩阵为


图3 平面3-RRR并联机构
(2)具有消极自由度的平面3-RRS机构。如果将图3机构的动平台4的3个R副变化为3个S副,就构成了一种具有消极自由度的平面3-RRS机构。仿上可得其构态变换矩阵:对应的具有消极自由度的平面3-RRS并联机构如图4所示。

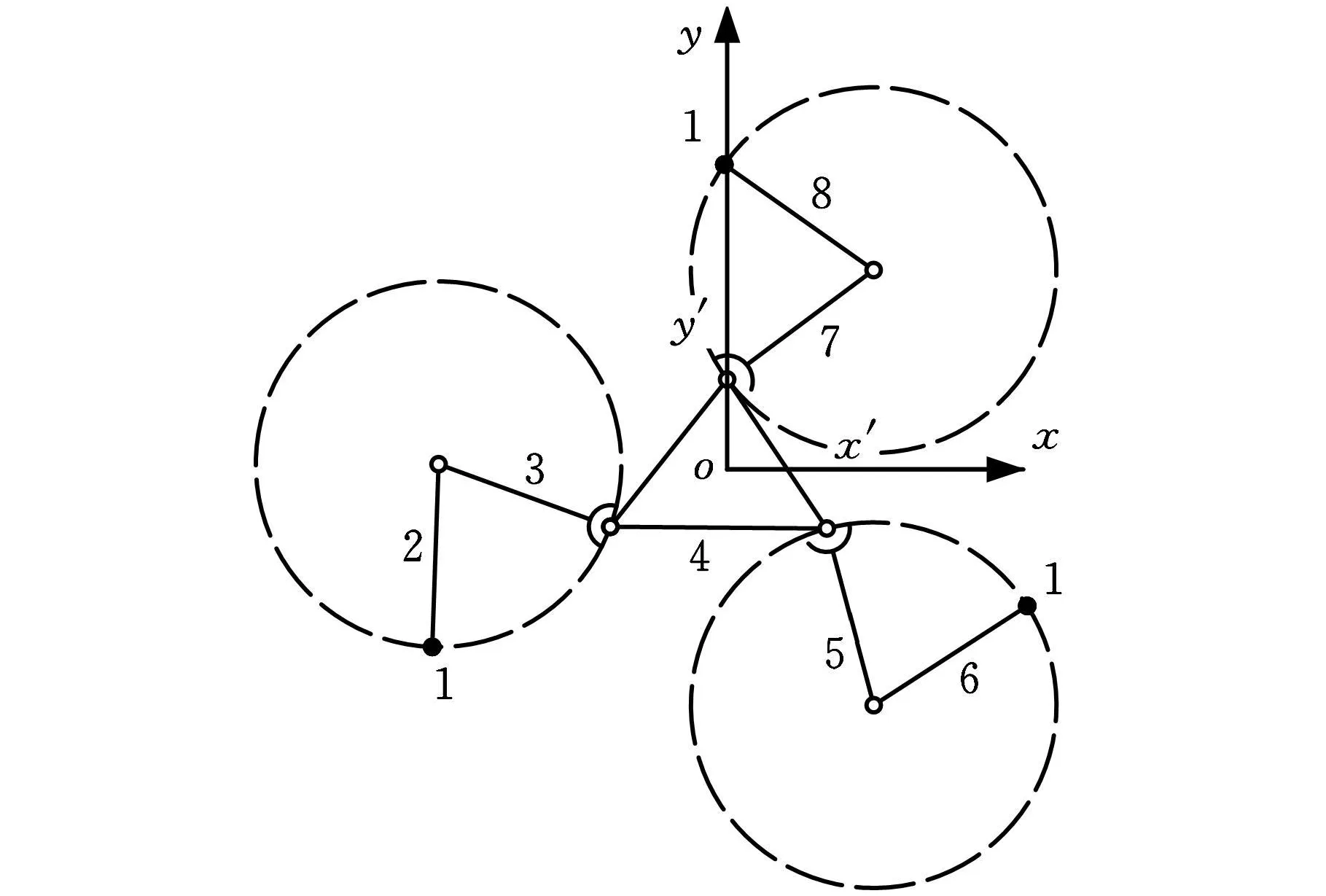
图4 具有消极自由度的平面3-RRS并联机构
3 运动副方位变胞
3.1 运动副方位变胞的基本概念
在图2所示的机构中,R副A和D轴线平行,构成了自由度为1的带有消极自由度的平面四杆机构。若改变该机构 A和D 轴线的方位,由平行到交错,则构成了图5所示自由度为1(带有局部自由度)的空间四杆机构。
可见,由图2机构到图5机构,构件数没变,运动副类型和数目没变,机构的自由度数也没变。但改变运动副D的轴线方位,便使机构由平面机构转化为空间机构。这种仅变换运动副轴线方位而使运动链运动空间改变,从而实现变胞的方式,称为运动副方位变胞。
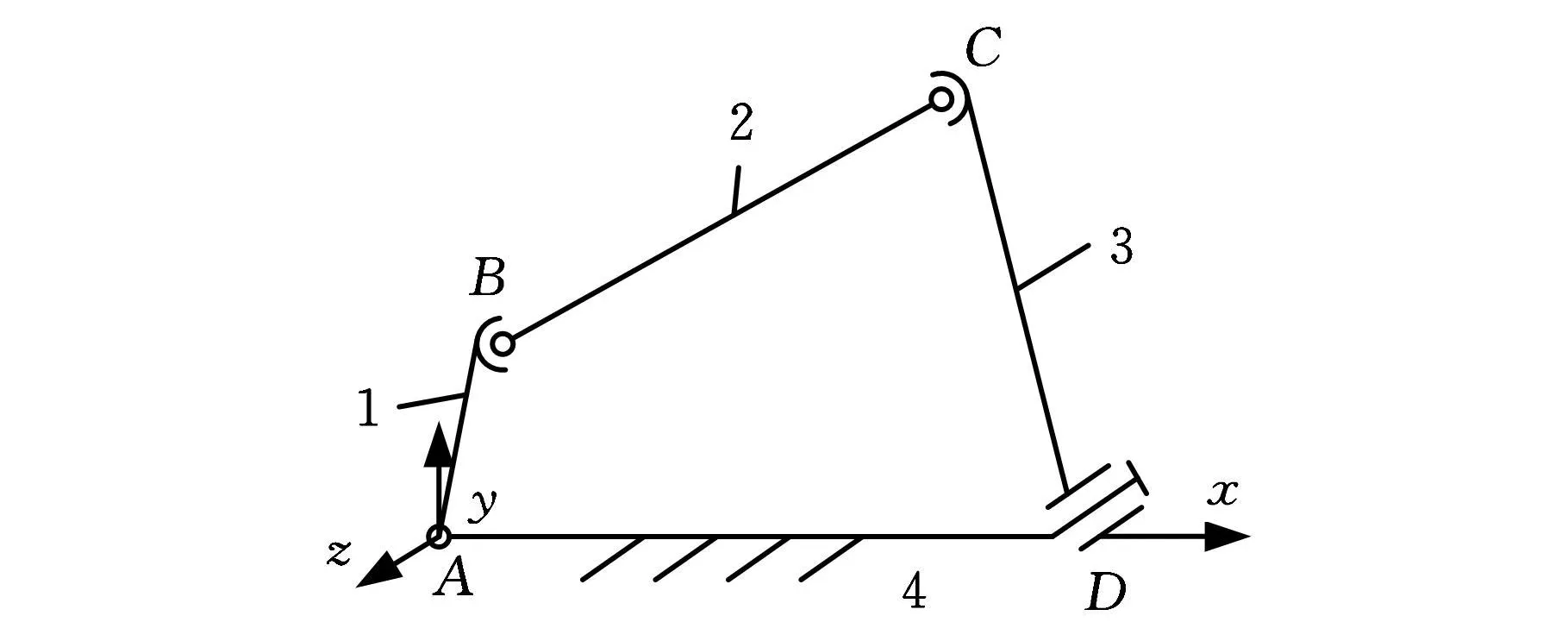
图5 空间RSSR四杆机构的运动简图
3.2 运动副方位变胞特点
运动副方位变胞具有下述特点:
(1)属于拓扑结构变胞,变胞的结果导致运动链运动空间的改变。如由平面运动链变化为空间运动链,或反之。
(2)变胞前后运动链的实际自由度不变,运动链的拓扑元素(构件数和运动副数)不变,但变胞过程会导致运动链中某些运动副的消极自由度与实际自由度间的转换。
3.3 运动副方位变胞条件
根据运动副方位变胞原理和特点,运动副方位变胞应具备如下基本条件:
(1)变胞前的运动链具有消极自由度,或变胞后的运动链产生消极自由度。
(2)方位变换运动副所在构件或分支在方位变化方向上具有自由度(变胞前为消极自由度,或变胞后产生消极自由度)。
3.4 运动副方位变换的实现
运动副方位变换可由Yan等[10]提出的具有变运动形式的运动副结构实现,或通过直接驱动运动副改变其轴线方位实现。
4 应用构态变换矩阵进行运动副方位变胞的方法
4.1 变胞方法和步骤
根据运动链构态变换矩阵(式(1)~式(3))各元素的意义及其性质,应用构态变换矩阵进行运动副方位变胞的基本方法和步骤如下:
(1)应用式(1)构造平面运动链的构态变换矩阵APlanar。
(2)构造与APlanar对应的具有消极自由度的平面机构的构态变换矩阵APlanar_passiveDOF。由APlanar向APlanar_passiveDOF转化时,应使变化前后的构件数不变,自由度数不变,运动副的个数不变,仅改变部分运动副的类型Jij和相应构件的轴线方位aij。由于变化的结果是机构的运动空间在平面与空间之间转换,因此 APlanar_passiveDOF的运动副的类型可根据下式计算:

式中,DOFP、DOFS分别为平面机构和空间机构的自由度;Pf为约束数为f的运动副的个数。
应该说明的是:式(6)等号两侧运动副提供的约束数应分别按平面和空间运动副计算。同时,为了方便起见,式(6)中没有涉及运动链中的虚约束等影响,仅为简化的运动链结构公式。如果在实际使用时有此类影响,还需按实际情况计算。由式(6)可知,对应给定的平面运动链APlanar的运动副的类型可能具有多种组合,可能代表对应的多个运动链。另外,根据对aij的定义,增加的多自由度运动副应选在变胞分支上。与改变后的J ij相关联的构件的轴线方位aij根据新的J ij由式(3)确定。
(3)构造变胞运动链的构态变换矩阵Am,即对APlanar_passiveDOF的 aij进行方位变换。由APlanar_passiveDOF向Am转化时,变化前后的构件数不变,自由度数不变,运动副的个数和类型不变,仅改变部分运动副的轴线方位aij。aij轴线方位的变化根据下述规则和步骤:①变换APlanar_passiveDOF中无消极自由度的运动副的轴线方位aij。由于步骤(2)使运动链增加的消极自由度是为了使运动链变胞时构件或分支在方位变化方向上具有自由度,因此不变换具有消极自由度的运动副的轴线。即选择由APlanar向APlanar_passiveDOF转化时轴线方位没有变化的aij进行方位变换。②选运动副的自由度较少的构件变换其轴线方位,并先选择机架、多副构件按顺序进行。自由度少即约束多的运动副的轴线的变化,牵连其构件或分支的结构变化,并导致整个运动链拓扑机构的变化,而且其结构简单,易于实施。而自由度多的运动副容易产生局部自由度,起不到变胞的效果,而且其结构复杂,实现困难。对于多环运动链,多副构件与各分支相互关联大,易实现运动链的整体变胞。③验证变胞前后运动链的自由度,使其自由度数不变。按上述①和②变换aij时,可能有多种组合,对应多种变胞方案,其中可能包括导致运动链失去自由度不符合运动副方位变胞原理的方案,需将其排除掉。④由Am构造变胞机构的运动简图。根据运动副方位变胞原理和构态变换矩阵各元素的意义,通常选运动副方位变化的构件为机架,构造对应机构的运动简图。
4.2 运动副方位变胞举例
4.2.1 单环运动链变胞
(1)根据式(1)~式(3),平面4R运动链的构态变换矩阵为

其自由度

(2)构造与AP_RRRR对应的具有消极自由度的平面机构的构态变换矩阵AP_RSSR_PassiveDOF。根据式(6),若选相邻两个球面副替代对应的转动副,则
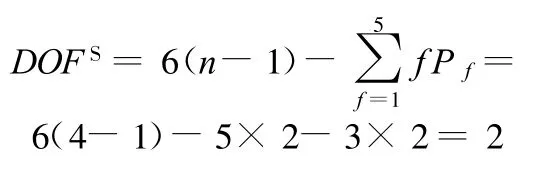
其中有一个局部自由度,实际自由度为1。可构造出对应的具有消极自由度的平面机构的构态变换矩阵:a14=1表明构件4上的2个转动副轴线平行,其中2个球副具有消极自由度。

(3)由AP_RSSR_PassiveDOF构造变胞运动链的构态变换矩阵AS_RSSR。变换构件4上一转动副的方位为任意方向,即使a14=4,则所求构态变换矩阵为
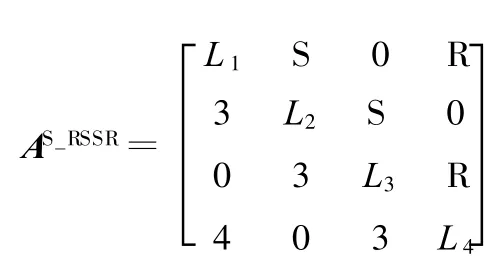
其自由度

其中包含一个局部自由度,实际自由度为1。AS_RSSR即为带有局部自由度的空间四杆机构的构态变换矩阵。由AS_RSSR可构造出对应的机构简图如图5所示。
如果变换构件1和构件4上运动副各轴方位使其共点,得带有消极自由度的球面RSSR运动链的构态变换矩阵:
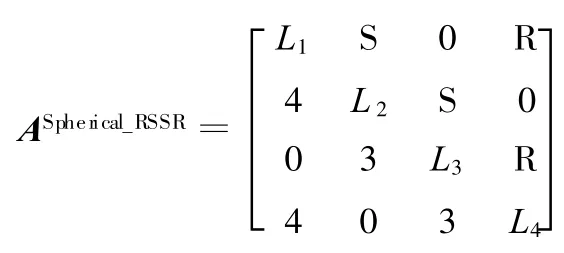
如果ASpherical_RSSR中2个球面副变换为转动副,得其构态变换矩阵:
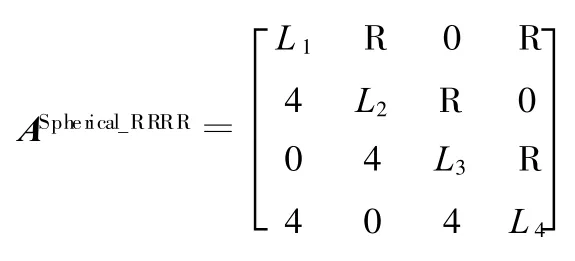
即球面RSSR运动链退化为球面4R运动链。
4.2.2 多环运动链变胞
图3所示为平面3-RRR并联机构的变胞,其主要步骤如下:
(1)构造平面3-RRS运动链的构态变换矩阵AP_3-RRR如式(4)所示。
(2)构造具有消极自由度的平面3-RRS机构的构态变换矩阵AP_3-RRS_PassiveDOF如式(5)所示。
(3)由AP_3-RRS_PassiveDOF构造变胞运动链的构态变换矩阵AS_3-RRS(即对应空间运动链的构态变换矩阵)。根据4.1节的变胞步骤(3),变换AP_3-RRS_PassiveDOF代表构件1各边2运动副轴线方位a26、a28、a68平行关系的1为任意相交关系的4,便构成空间3-RRS的构态变换矩阵AS_3-RRS:

由AS_3-RRS可知,n=8,P 3=3,P5=6。其自由度为:DOFS=6×7-3×3-5×6=3,验证了其自由度数与平面3-RRR机构相同,即构成空间3-RRS并联运动链。将AS_3-RRS按式(1)连接方式,如按文献[9]设计的转动副结构形式(图6a),或直接驱动运动副模块改变其轴线方位(图6b),若选构件1为机架,可构造其运动简图如图7所示。

图6 用于方位变胞的两种转动副结构形式
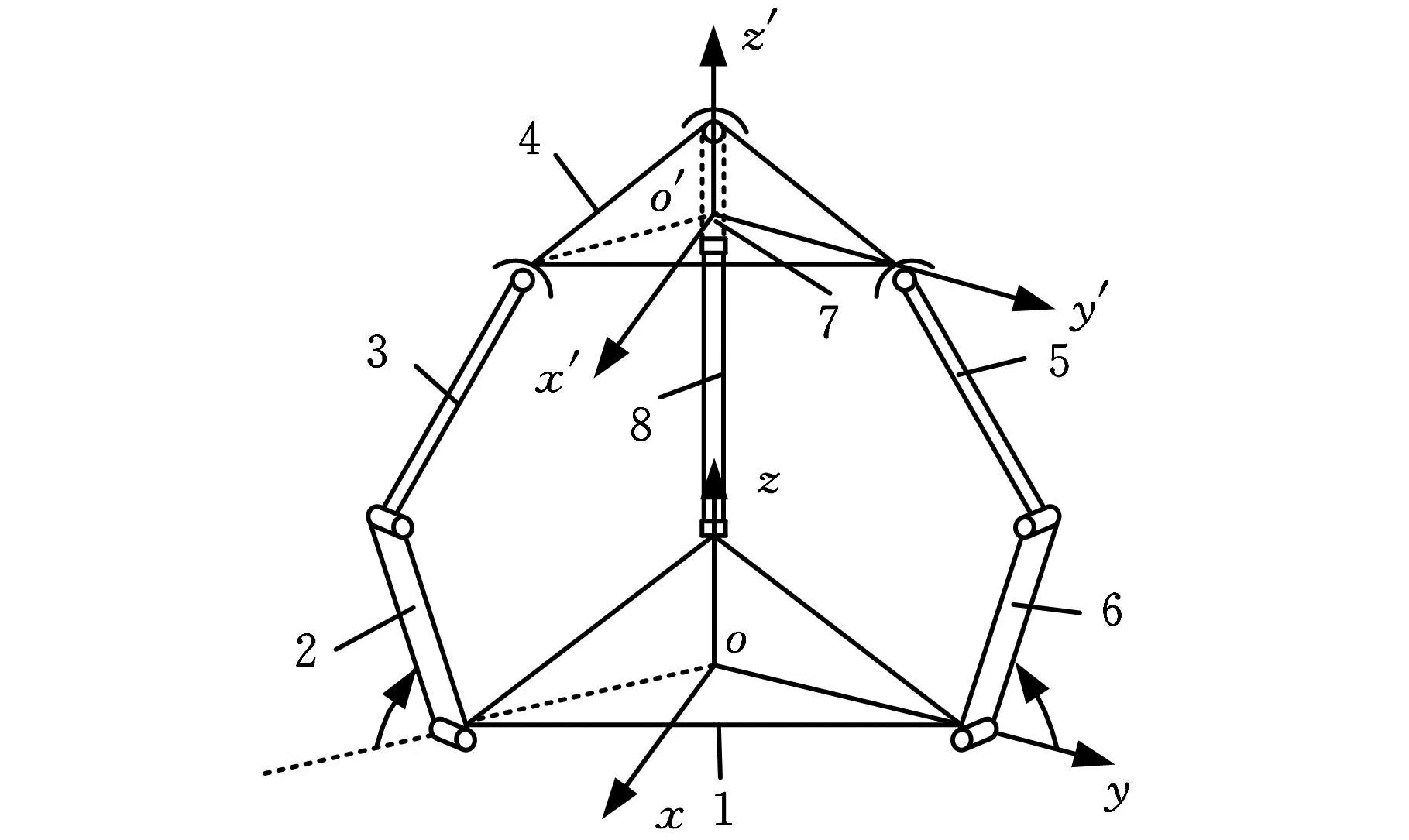
图7 空间3-RRS并联机构简图
5 结束语
本文构造了一种描述变胞机构构态演化的构态变换矩阵,提供了运动链连接状况、运动副类型和运动副方位特征信息。该构态变换矩阵不仅可用于运动副方位变胞问题的研究,也可用于其他类型变胞问题和一般的运动链综合问题研究,具有普遍的理论和实用意义。
给出了一种基于构态变换矩阵的运动副方位变胞的方法和步骤,通过运动副方位变胞,可实现机构运动空间在平面与空间之间的转换,进一步丰富了变胞机构的变胞方法。
另外,根据式(1),只要运动链的构件编号和起点确定,运动链的拓扑关系就确定了,因此,该矩阵也可推广用于运动链或机构的同构体的判别。
[1] Dai JS,Jones J R.Mobility in Metamorphic Mechanisms of Foldable/Erectable Kinds[J].Journal of Mechanical Design,1999,121(3):375-382.
[2] Dai J S,Rees J J.Configuration Transformations in Metamorphic Mechanisms of Foldable/Erectable Kinds[C]//In Proc.of 10th World Congress on the Theory of Machines and Mechanisms.Oulu,1999:542-547.
[3] Carroll D W,Magleby S P,Howell L H.Simplified Manufacturing Through a Metamorhic Process for Compliant Orthoplanar Mechanisms[C]//ASME 2005 International Mechanical Engineering Congress and Exposition.Orlando,2005:389-399.
[4] Liu C H,Yang T L.Essenceand Characteristics of Metamorphic Mechanisms and Their Metamorphic Ways[C]//In Proc.11th World Congress in Mechanism and Machine Science.Tianjing,2004:1285-1288.
[5] 戴建生,丁希仑,邹慧君.变胞原理和变胞机构类型[J].机械工程学报,2005,41(6):7-12.
[6] 戴建生,丁希仑,王德伦.一空间变胞机构的拓扑结构变换和对应的矩阵演算[J].机械工程学报,2005,41(8):30-35.
[7] Dai JS,Rees JJ.Matrix Representation of Topological Changes in Metamorphic Mechanisms[J].Transactions of the ASME:Journal of Mechanical Design,2005,127(4):610-619.
[8] 王德伦,戴建生.变胞机构及其综合的理论基础[J].机械工程学报,2007,43(8):32-42.
[9] Yan H S,Kuo C H.Topological Representations and Characteristics of Variable Kinematic Joints[J].Transactions of the ASME Journal of Mechanical Design,2006,128(2):384-391.
[10] 李树军,宋贵秋,杜立群,等.用拓扑特性矩阵辨识运动链的同构体及机架变换研究[J].机械工程学报,2002,38(1):149-153.
[11] Li S J.Computer-aided Structure Synthesis of Spatial Kinematic Chains[J].Mech.Mach.Theory,1990,25(6):645-653.
[12] 杨廷力.机器人机构拓扑结构学[M].北京:机械工业出版社,2004.
[13] 李树军,戴建生,王德伦.含环路布局和运动副方位特征的运动链拓扑结构描述[J].机械工程学报,2009,45(6):34-40.
