基于预处理共轭梯度的大地电磁快速正演

张继锋 ，汤井田，王烨，肖晓

(1. 长安大学 地质工程与测绘学院，陕西 西安，710054；2. 中南大学 信息物理工程学院，湖南 长沙，410083)

大地电磁方法因具有成本低、工作方便、不受高阻层屏蔽等优点，已广泛应用于深部地球物理勘探以及石油天然气等能源的勘查。由于有限元方法具有模拟复杂地形的能力，适应性比较强，其应用越来越广泛。Coggon[1]利用能量最小化原理推导了电磁变分方程，采用低阶次三角形单元对半空间下二维地电结构进行了有限元数值模拟；Wannamaker等[2]研究了二维带地形的大地电磁正演问题；Key等[3]采用非结构化网格的自适应有限元对二维地电模型进行了模拟；陈小斌等[4-9]采用有限元法研究了大地电磁的二维正演问题。这些研究主要从方法或计算精度上进行了探讨，对于如何压缩存储和快速求解等问题，张永杰等[10-14]研究了系数矩阵的存贮和ICCG方法(不完全Cholesky分解预处理共轭梯度法)的求解，但仅限于实数范围；Smith等[15-16]研究了双共轭梯度法的求解，谢德馨等[17-18]研究了电磁场分析中大型复系数方程组的求解，但大都是针对非地球物理电磁场进行研究。在此，本文作者从地球物理电磁场中大地电磁二维正演出发，采用全稀疏按行压缩存储方式，把不完全LDLT(改进的 Cholesky分解)应用于矩阵的预处理，结合共轭梯度迭代法快速求解大型稀疏复系数方程组，以实现二维大地电磁的快速正演模拟。

1 二维大地电磁有限元正演

假定地下电性结构是二维的，取走向为 z轴，x轴与 z轴垂直，保持水平，y轴垂直向上。当平面电磁波以任意角度入射地面时，地下介质中的电磁波总以平面波形式几乎垂直向下传播。将麦克斯韦方程组中的2个旋度方程按分量展开，并考虑到0/=∂∂z，得2个独立的方程组，分别命名为TE模式和TM模式，可统一表示为式中：Ez为电场的z轴分量；Hz为磁场的z轴分量；σ为地下介质的电导率；ω为角频率；μ为大地的磁导率；ε为介质的介电常数。式(4)即为有限元正演所依赖的变分公式。其中：是上边界；是下边界；侧边界为齐次边界条件，不予以考虑。

2 压缩存储

传统的一维变带宽或二维定带宽存储方式只存储带宽内的所有元素，节省了许多存储空间，但即使在带宽内，也包含着大量的元素 0，若节点的编号很不规则，则会形成1个非带状的矩阵，不能采用该存储方式。按行压缩存储方案，根据有限元刚度矩阵大型稀疏的特性，仅存储刚度矩阵中的非零元素，不需要考虑带宽和网格的划分规则，大大节省了存储空间，而且在使用迭代法求解时，元素0不参与运算，节省了计算时间，特别适合于各种高效快速的迭代方法求解。

按行压缩是把刚度矩阵中的非零元素按行依次存储在1个一维数组中，然后，通过2个索引数组以确定该一维数组中的元素与原矩阵中元素的对应关系。假设有1个稀疏系数矩阵M(如式(5)所示)，其中大部分元素为0，通过3个数组a，ia和ja存储该矩阵中的非零元素。首先，把该矩阵中的非零元素按行依次存储在数组a中；然后，通过索引数组ia和ja确定数组a中的元素在矩阵M中具体位置： ja表示列索引，即a(k)=M(i, j)，那么 ja(k)=j；ia表示行索引，若 M(i, j)是第i行第一个非零元素，并且a(k) = M(i, j)，则ia(i)= k。这样，数组a就和矩阵M建立了一一对应关系，为各个元素参与共轭梯度法迭代求解提供了基础。稀疏矩阵按行压缩存储表见表1。

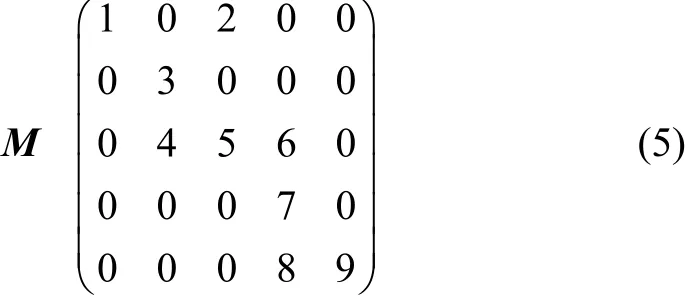
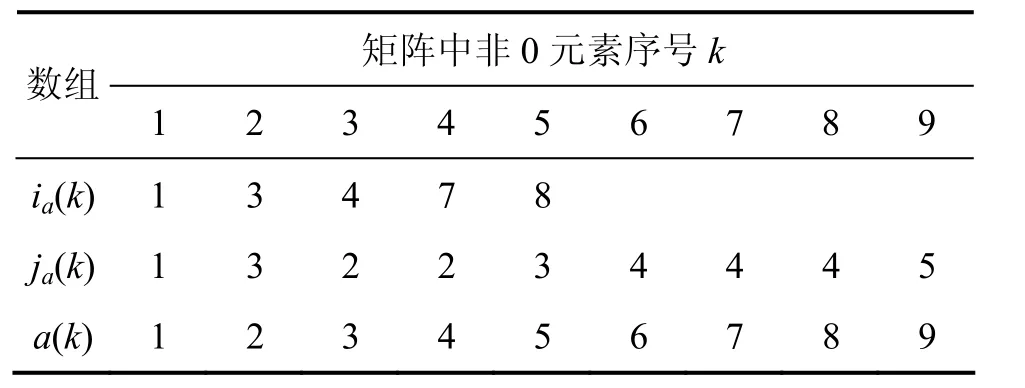
表1 稀疏矩阵按行压缩存储表Table 1 Row compressed store for sparse matrix

上例直观地给出了矩阵的元素，可以很清楚地看到哪些是非零元素。但是，实际有限元程序的编制中直观的刚度矩阵并不存在，所以，必须了解非零元素在刚度矩阵中的位置，以便真正实现按行压缩存储方案，其基本步骤归纳如下：

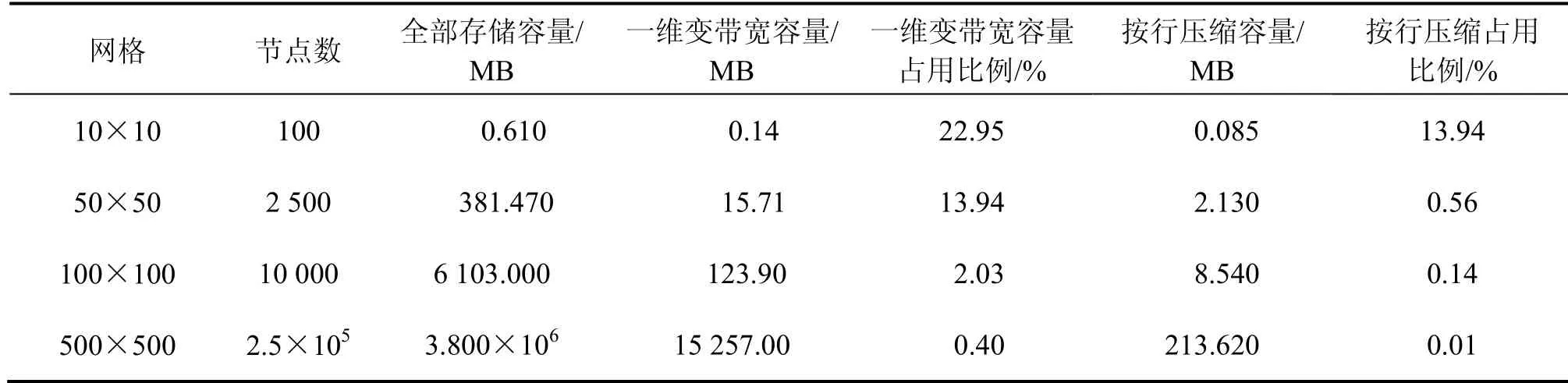
表2 二维不同存储方法的存储量比较Table 2 Comparison of memory capacitance for two dimensional different store methods

(1) 寻找包含第 i (i=1, 2, …, m)个节点的所有单元。

(2) 找出与节点i相关的所有节点，然后对其进行排序，相同的节点只出现1次。

(3) 确定节点的稀疏关系。

(4) 把所有单元刚度矩阵组装加到全局刚度矩阵中。

为了更直观地看到压缩存储对于节省内存空间的优越性，将一维变带宽存储对规则的四边形网格划分形成的系数矩阵的存储量进行比较，如表2所示。

从表2可以看到：随着网格节点数增多，压缩比例越来越大，也就是说，刚度系数矩阵越大，越利于压缩存储。所以，在进行大型的有限元计算时，必须进行压缩存储，才能够有效地利用存储空间；其次，按行压缩的存储量随着网格节点的增加，其压缩比例急剧增大，远远优于一维变带宽存储。这是因为按行压缩只存储非零元素，方程组的系数矩阵不断增大，而每一行的非零元素变化不大，所以，它的压缩量最大，充分显示了有限元系数矩阵的稀疏性。

3 预处理共轭梯度

3.1 不完全LDLT预处理

有限元方法中最后形成的大型系数矩阵常常具有很大的条件数，是一个非常病态的矩阵。对于这种矩阵，若直接采用共轭梯度法，则收敛速度非常慢，甚至不收敛，所以，必须采取合适的预处理方法，通过改变矩阵的一些关键元素值，降低矩阵的条件数，使共轭梯度法能够顺利迭代，提高其收敛速度。这里采用不完全 LDLT预处理，避免开方运算，可用于非正定方程组的求解。

首先，把LDLT具体的算法简要陈述为：

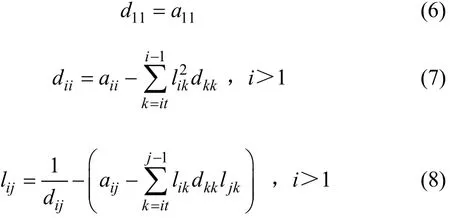
其中：dii为分解后对角阵元素；lij为分解后下三角阵元素；aij为原始矩阵元素。

但是，在LDLT预处理过程中，产生的L矩阵是1个稠密矩阵，原来的系数矩阵稀疏性被破坏，这与压缩存储的思想不符，所以，必须采用不完全 LDLT分解法，使存储量和改善系数矩阵性态之间达到平衡。

3.2 基于LDLT预处理共轭梯度法

给定1个初始猜想的x0，有

对i=0, 1, 2, …，进行如下计算：

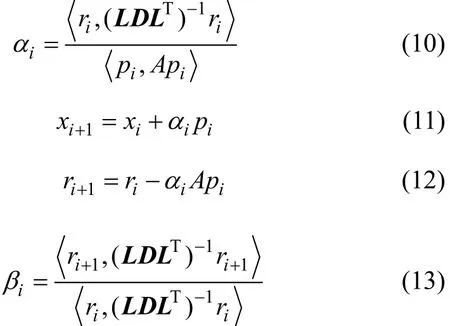
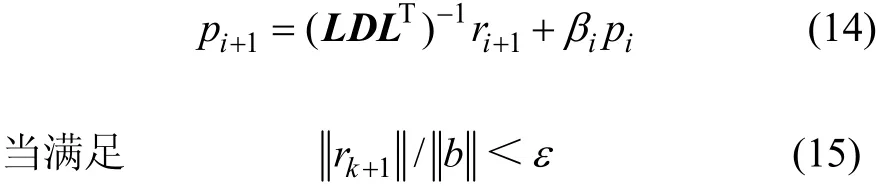
时迭代停止。其中：iα，1+ix，1+ir，iβ和1+ip表示第i次迭代的值；ε为迭代误差的判断值；〉〈βα,表示α与β的内积。

3.3 逆矩阵与向量乘积的快速计算

以上算法式中，存在(LDLT)-1与任一向量的乘积，运算时间长。如何快速高效地求解(LDLT)-1r是预处理共轭梯度法速度的关键。为了解决此问题，设

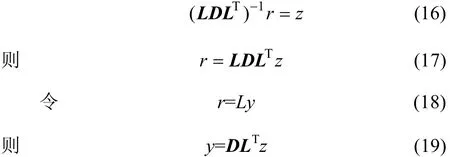
可见：把(LDLT)-1r转换为求解2个线性方程组，由于L是一个下三角阵，且仅存非零元素，因而，以上顺代和回代仅涉及少量的非零元素的乘积和加法运算，求解非常迅速。

3.4 数值算例

针对预处理共轭梯度算法，编制相应的程序，并且在计算机上进行验证。计算机配置内存为2G，主频为2.26 Hz，硬盘容量150 Gbyte。图1和图2所示是不同自由度下共轭梯度法的收敛速度，可以看出：ILDLT预处理共轭梯度法收敛速度非常快，但在收敛过程中，迭代误差会上下波动，最终收敛到准确解。计算时间和迭代次数见表3。从表3可以看出：采用该方法计算上万个自由度的大型复系数方程组，时间在1 s之内，这表明本文算法非常高效。

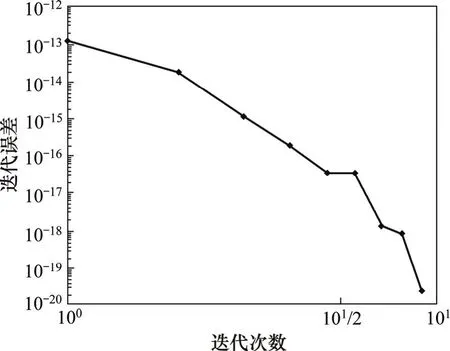
图1 2 925个自由度的ILDLTCG收敛率Fig.1 ILDLTCG convergence rate of 2 925 degree of freedom

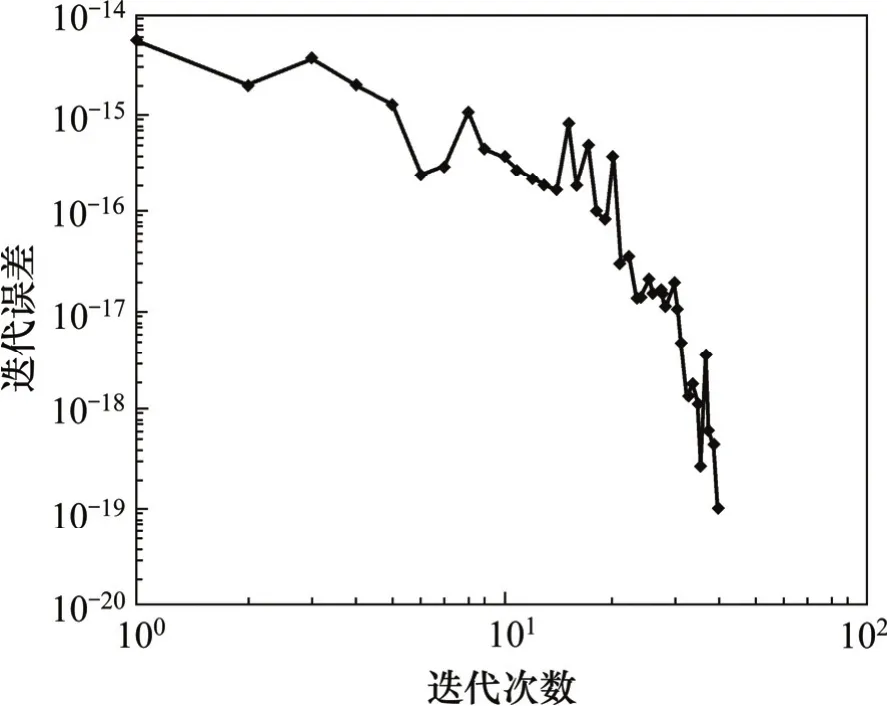
图2 13 020个自由度的ILDLTCG收敛率Fig.2 ILDLTCG convergence rate of 13 020 degree of freedom

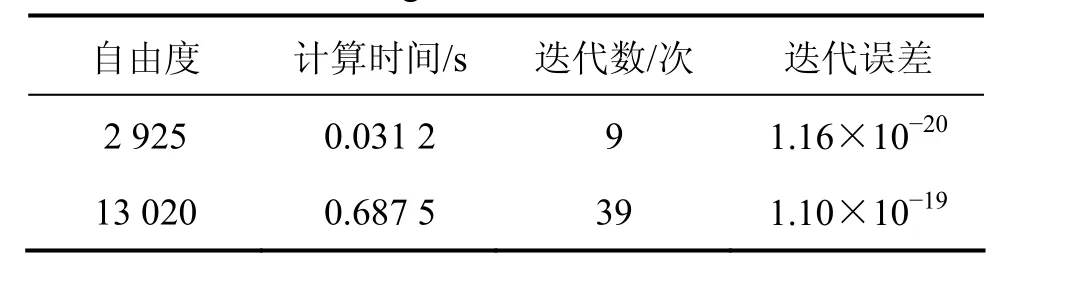
表3 自由度不同时的计算时间及迭代次数Table 3 Computation time and iteration number for different degrees of freedom

4 地电模型正演

为了检验程序的正确性，建立了1个层状模型，分别对二维大地电磁的2种极化模式进行计算，并与解析解进行对比。模型层电阻率分别为：ρ1=10 Ω·m，ρ2=100 Ω·m，ρ3=10 Ω·m，ρ4=100 Ω·m，ρ5=10 Ω·m；层厚度分别为：h1=300 m，h2=700 m，h3=1 500 m，h4=3 100 m。采用如下40个频点：320，240，160，120，80，60，40，30，20，15，10，7.5，6.0，4.5，3.0，2.25，1.5，1.125，0.75，0.562 5，0.375，0.281 25，0.187 5，0.140 625，0.093 75，0.070 312 5，0.046 875，0.035 156 25，0.023 437 5，0.017 578 125，0.011 718 75，0.008 789 062 5，0.005 859 375，0.004 394 531 25，0.002 929 687 5， 0.002 197 265 625，0.001 464 843 5，0.001 098 632 5，0.000 732 421 75，0.000 549 316 25。地电模型的视电阻率曲线和相应曲线分别见图 3和图4。

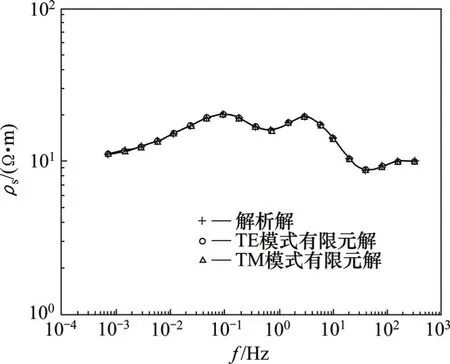
图3 地电模型的视电阻率曲线Fig.3 Curve of apparent resistivity for geo-electrical model

图4 地电模型的视相位曲线Fig.4 Curve of apparent phase for geo-electrical model

经计算，对于TE模式和TM模式，视电阻率ρs平均相对误差分别为 0.384%和 0.374%，最大相对误差分别为 1.299%和 2.029%；视相位φ平均相对误差分别为0.108%和0.122%，最大相对误差分别为0.320%和0.663%，而且最大相对误差都出现在极低频段。

5 结论

(1) 按行压缩存储1万个自由度矩阵时，压缩率达到 99.9%以上，比常规的变带宽存储方法节省了大量内存空间，而且矩阵越大，压缩比例越大，尤其有利于存储超大型稀疏矩阵。

(2) 不完全 LDLT预处理极大地提高了共轭梯度法的收敛速度，使得求解1万个自由度的方程组时所用时间在1 s以内。

(3) 建立了大地电磁层状模型，分别对TE模式和TM模式2种极化方式进行了数值模拟，并与解析解进行比较，结果表明：采用大地电磁层状模型计算精度高，平均相对误差在0.5%以内，为快速精确反演提供了保证。

[1] Coggon J H. Electromagneic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-155.

[2] Wannamaker P E, Stodt J A, Rijo L. A stable finite element solution for two-dimensional magnetotelluric modeling[J].Geophysical Journal International, 1987, 88(1): 277-296.

[3] Key K, Weiss C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example[J].Geophysics, 2006, 71(6): 291-299.

[4] 陈小斌. 有限元直接迭代算法[J]. 物探化探计算技术, 1999,21(2): 165-171.CHEN Xiao-bin. Direct iterative algorithm of finite element[J].Computing Techniques for Geophysical and Geochemical Exploration, 1999, 21(2): 165-171.

[5] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社,1994: 229-247.XU Shi-zhe. Finite element method in geophysics[M]. Beijing:Science Press, 1994: 229-247.

[6] 陈小斌, 张翔, 胡文宝. 有限元直接迭代算法在 MT二维正演计算中的应用[J]. 石油地球物理勘探, 2000, 35(4): 487-496.CHEN Xiao-bin, ZHANG Xiang, HU Wen-bao. Application for direct iterative algorithm in MT 2D forward computation[J]. Oil Geophysical Prospecting, 2000, 35(4): 487-496.

[7] 史明娟, 徐世浙, 刘斌. 大地电磁二次函数插值的有限元正演模拟[J]. 地球物理学报, 1997, 40(3): 421-430.SHI Ming-juan, XU Shi-zhe, LIU Bin. Finite element method using quadratic element in MT forward modeling[J]. Chinese J Geophys, 1997, 40(3): 421-430.

[8] 马为, 陈小斌, 赵国泽. 大地电磁测深二维正演中辅助场的新算法[J]. 地震地质, 2008, 30(2): 525-533.MA Wei, CHEN Xiao-bin, ZHAO Guo-ze. A new algorithm for the calculation of auxiliary field in MT 2D forward modeling[J].Seismology and Geology, 2008, 30(2): 525-533.

[9] 刘小军, 王家林, 于鹏. 基于二次场的二维大地电磁有限元数值模拟[J]. 同济大学学报, 2007, 35(8): 1113-1117.LIU Xiao-jun, WANG Jia-lin, YU Peng. Secondary field based on two dimensional magnetotelluric numerical modeling by finite element method[J]. Journal of Tongji University, 2007,35(8): 1113-1117.

[10] 张永杰, 孙秦, 李江海. 大型稀疏线性方程组的改进ICCG方法[J]. 计算物理, 2007, 24(5): 581-584.ZHANG Yong-jie, SUN Qin, LI Jiang-hai. An improved ICCG method for large scale sparse linear equations[J]. Chinese Journal of Computational Physics, 2007, 24(5): 581-584.

[11] 张永杰, 孙秦. 大型稀疏线性方程组新的ICCG方法[J]. 数值计算与计算机应用, 2007, 43(36): 19-20.ZHANG Yong-jie, SUN Qin. Preconditioned biconjugate gradient method of large-scale complex linear equations[J].Computer Engineering and Applications, 2007, 43(36): 19-20.

[12] 张永杰, 孙秦. 大型稀疏线性方程组的全稀疏存贮策略[J].陕西理工学院学报: 自然科版, 2005, 21(4): 67-68.ZHANG Yong-jie, SUN Qin. Fully sparse strategy of large scale linear equations[J]. Journal of Shaanxi University of Technology:Natural Science Edition, 2005, 21(4): 67-68.

[13] 吴小平, 徐果明, 李时灿. 解大型稀疏方程组的ICCG方法及其计算机实现[J]. 煤田地质与勘探, 1999, 27(6): 54-56.WU Xiao-ping, XU Guo-ming, LI Shi-can. ICCG Method for solving large sparse equations and its computer programming[J].Coal Geology & Exploration, 1999, 27(6): 54-56.

[14] 陈志, 高旅端. 求解大规模稀疏线性方程组的算法[J]. 北京工业大学学报, 2001, 27(3): 262-265.CHEN Zhi, GAO Lü-duan. An algorithm for solving large-scale sparse group of linear equations[J]. Journal of Beijing Polytechnic University, 2001, 27(3): 262-265.

[15] Smith J T. Conservative modeling of 3-D electromagnetic fields,Part II bi-conjugate gradient solution and an accelerator[J].Geophysics, 1996, 61(5): 1319-1324.

[16] 吴海容. 复双共轭梯度法的结构[J]. 电机与控制学报, 1996,19(2): 133-141.WU Hai-rong. Structure of the complex bi-conjugate gradient method[J]. Electric Machines and Control, 1996, 19(2):133-141.

[17] 谢德馨, 姚缨英, 白保东. 电磁场分析中大型稀疏对称线性方程组预处理法的改进[J]. 电机与控制学报, 1997, 1(2):98-101.XIE De-xin,YAO Ying-ying, BAI Bao-dong. The modified preconditioning approach for large sparse symmetric linear systems in electromagnetic field analysis[J]. Electric Machines and Control, 1997, 1(2): 98-101.

[18] 文代刚, 姜可薰, 黄键. 求解有限元复代数方程组的实型ICCG法[J]. 电工技术学报, 1996, 11(4): 62-65.WEN Dai-gang, JIANG Ke-xun, HUANG Jian. Real type of ICCG method for complex algebraic equations of FEM[J].Transaction of China Electrotechnical Society, 1996, 11(4):62-65.