约束优化求解作业车间调度问题研究

杨宏安 孙启峰 郭 杰

西北工业大学，西安，710072

0 引言

作业车间调度问题（job shop scheduling pr oblems，JSSP）实质是调度优化问题，而调度优化问题又属于一类典型的约束优化问题。近年来，近似调度方法（如遗传算法、禁忌搜索、模拟退火和免疫算法等）是国内JSSP研究领域的主流方法，其调度模型基本上都可以视为在满足工艺路线、机床能力和交货期等约束条件下的单／多目标优化问题，而求解方法均属于启发式搜索。由于JSSP属于典型的NP困难问题，且实际生产车间具有大规模、多任务、多资源、多约束和动态随机性等特点，近似调度方法真正应用于指导企业生产实践的成功案例较少。

约束优化问题（constrained opti mization problems，COP）是在约束满足问题（constraint satisfaction proble ms，CSP）基础上发展而来的。CSP方法以满足实际问题的所有约束条件为出发点，在其模型中不包含目标函数；而COP和CSP的本质区别是在模型中引入了目标函数，从而使之更贴近调度优化问题，同时也使得该类问题的求解复杂度显著提高。作为人工智能中相当活跃的研究领域，CSP／COP能很好地描述智能领域的组合、调度和规划等复杂问题，尤其适合于描述和求解大规模的组合优化问题。

确定型JSSP和COP都是在事先已知变量和约束的前提下，寻求变量的合理取值，并在满足所有约束的前提下优化特定的目标函数，因此，作业车间调度问题和约束优化问题的相似性和吻合度较高。Fox［1］首次将CSP方法引入车间调度问题研究之中，并在此基础上开发出基于启发搜索技术的ISIS调度系统［2］。Smith等［3］于20世纪90年代初开发完成基于Macro－Opport unistic的OPIS调度系统。Sadeh在变量／值排序启发算法［4］和 回 溯 处 理［5］等 方 面 进 行 了 深 入 研 究。Barták等［6］近年来在基于约束规划的计划和调度方面开展了大量研究工作。

国内将CSP方法应用于求解JSSP的相关文献较少。文献［7－9］对基于约束满足的车间调度进行了综述。文献［10］针对Job Shop调度问题，采用形式化的约束一致性实施、操作选择策略、开始时间选择策略和不完全回跳策略来提高约束满足调度算法的求解效率。文献［11］针对作业车间排序重调度问题，提出了一种可分布求解的分级模型，并对分级模型采用改进的修复约束满足算法进行求解。

目前，国内已开始将CSP方法引入到JSSP的研究中，但CSP方法仅以求得调度问题的满意解为出发点，而没有涉及调度目标函数的优化问题。本文以CSP方法为基础，将提前／拖期优化指标引入CSP中，使约束满足问题升级为约束优化问题；基于COP和JSSP的吻合度考虑，将作业车间调度问题转化为约束优化问题，综合运用COP的四元组建模方法和回溯搜索方法对JSSP进行模型描述和算法求解，旨在构建从模型描述、调度策略设计、调度算法设计和仿真试验在内的约束优化技术求解JSSP的完整研究框架，并为后续进一步深入研究约束优化调度引擎搭建基础性支撑平台。

1 约束优化问题

定义1 约束优化问题由一个变量集、变量值域、约束集和目标函数组成，可视为一个四元组P ＝ （V，D，C，O）。其中，V 为变量集，V ＝ ｛V1，V2，…，Vn｝；D为各变量的候选值域集，D ＝ ｛D1，D2，…，Dn｝，C 为变量之间的约束集，C ＝ ｛c1，c2，…，cm｝，O 为目标函数。

定义2 约束优化问题的解是在满足全部约束集C的条件下，在变量集V内寻求一组变量赋值｛a1，a2，…，an｝并使得目标函数O取得最优，其中ai∈Di。

2 约束优化调度模型

2．1 相关变量说明

对于调度任务池内的任意零件Ji，假设Ji的任一加工工序为Oli，其中，i＝1，2，…，n；l＝1，2，…，m；n为零件数量，m为零件Ji内的工序数量。表1、表2分别为零件Ji和工序Oli的相关加工参数定义。

表1 零件J i相关参数定义

表2 工序Oli相关参数定义

2．2 约束优化调度模型

根据定义1，采用COP的四元组分析方法来构建约束优化调度模型。

2．2．1 变量集

作业车间调度的根本任务是确定各零件加工工序在机床上的开工时间，因此，变量集的构造直接以调度任务池内各零件的加工工序作为独立决策节点，变量定义为任意零件Ji的任一工序Oli的开工时间stli。

2．2．2 约束集

对于离散加工型车间而言，一个可行调度方案的先决条件是满足工艺路线和机床能力两类硬约束，另外，零部件交货期约束也是保证整机配套和成品交付的必备条件。

（1）工艺路线约束。该约束描述了同一零件内不同工序之间的时序关系。假设在零件Ji内，Oli是工序Oji的下游工序，则工艺路线约束为stji＋duji≤stli。

（2）机床独占性约束。该约束描述了承制机床上加工工序队列的时序关系。假设工序Oli和Okj由同一机床加工，则二者之间的机床独占性约束为（stli＋duli≤stkj）∨ （stjk＋dujk≤stli）。

（3）时间约束。该约束描述了某一零件的释放期（或投料期）和交货期约束。对于零件Ji，其首道工序O1i和末道工序Omi的开工时间应满足Ji的可接受最早释放期和可接受最晚完工时间约束：（st1i≥er di）∧ （stmi＋dumi≤lcdi）。

2．2．3 目标函数

（1）提前／拖期调度成本。针对调度任务池内的任一零件Ji，存在以下拖期、库存调度成本：①拖期成本，零件Ji的拖期成本Tar di＝tar di×max（0，Ci－ddi），其中，tar di为Ji的拖期惩罚系数。②库存成本包括零件的在制品流动成本和成品库存成本两部份。其中，在制品流动成本定义为零件从投料开始至实际加工结束之间的现场在制品积压成本。零件Ji的库存总成本Invi＝ddi－Ci），其中，invli为工序Oli的在制品库存成本系数。

（2）调度目标。在计算出任意零件Ji的拖期和提前成本后，整个调度任务集的调度总成本ScheduleCost调度目标则是在满足上述所有约束集的前提下，在各工序开工时间值域内寻求一组合理取值，使得调度总成本ScheduleCost最小。

2．3 基于约束传播的变量值域初始化方法

上述约束优化调度模型业已构造完成COP四元组中的变量集、约束集和目标函数，而变量值域即为各工序开工时间的候选取值时间窗口。初始搜索状态下的工序开工时间值域依据约束传播方法产生。

约束传播方法：各工序最早开工时间根据零件的最早可接受释放期沿工艺路线向下游工序依次顺序传播，而工序最晚开工时间则依据零件的最晚可接受完工时间沿工艺路线向上游工序依次倒序传播，从而即可确定各工序的开工时间窗口。以工序Oli为例，其初始搜索状态下的开工时间值域计算如下：

式中，estli＋1为Oli的下道工序的最早开工时间；lstil－1为Oli的上道工序的最晚开工时间。

3 约束优化调度策略设计

3．1 两阶段调度策略

JSSP属于典型的NP困难问题，传统调度优化方法很难满足大规模调度对模型描述和计算效率的更高需求。因此，为降低大规模JSSP的求解复杂度和提高调度算法的实用性，遵循解决实际工程问题的思维模式和原则，将求解大规模JSSP划分为“瓶颈机床识别”和“单机排序优化”两个阶段，即在各搜索空间内，首先计算和识别出当前状态下的瓶颈机床，然后以该瓶颈机床为载体，对竞争该机床的多个工序采用单机排序优化方法进行处理。这种贴近生产实际的处理策略可以有效降低多机排序优化的复杂度，从而使得求解大规模JSSP的困难度显著较低。

3．2 动态修订搜索空间策略

因工艺路线和机床独占性两类硬约束的存在，已调度工序的赋值结果势必影响剩余搜索空间内相关工序的开工时间值域，进而对下一搜索空间内的瓶颈机床识别、变量排序和值排序等环节产生连锁影响。因此，引入动态修订搜索空间的调度策略，根据已调度中间结果和约束集，调整和过滤剩余搜索空间各工序开工时间的值域，及时修订搜索空间的概率计算，以保证启发规则始终指向于当前搜索状态下的瓶颈机床，从而为第二阶段的单机排序优化提供计算依据。

4 “Thrashing”现象消减机制

“Thrashing”现象是指在回溯算法搜索过程中频繁发生约束冲突的现象。“Thrashing”现象的存在严重制约回溯搜索的求解效率，并有可能导致回溯搜索进程陷入死循环。文献［12］通过大量调度实例发现：采用CSP方法求解调度问题时，绝大多数问题属于两类情况：一类是无回溯求解调度问题，另一类则是搜索进程频繁出现“Thrashing”现象。

大规模JSSP具有约束松驰度紧、约束内联度高等特征，回溯发生不可避免。因此，关注“Thrashing”、减小“Thrashing”发生概率是设计回溯搜索算法时不可回避的重要环节。在约束优化调度算法设计时，可采用一致性预处理机制和回溯前移机制来减少“Thrashing”频发。

（1）一致性预处理机制。随着调度进程的推进，由于已调度工序开工时间的确定，受约束优化调度模型中两类硬约束的影响，剩余调度空间中与已调度工序相关的变量值域势必包含潜在冲突值，而这些潜在冲突值的存在可能导致后续搜索过程发生约束冲突。因此，通过采用一致性预处理机制，依据已调度中间结果对剩余搜索空间相关变量集的值域预先实施修剪和过滤，以剔除其值域内的潜在冲突值，从而减少剩余变量值域发生约束冲突的概率。

（2）回溯前移机制。约束集在回溯搜索过程中存在“前紧后松”的特点，即在搜索初期，工序变量之间的约束松弛度较紧，而随着调度进程的推进，在前期满足瓶颈机床和关键工序变量赋值后，后期的搜索过程则呈现约束相对较松的特点。因此，采用回溯前移机制，将搜索进程发生约束冲突的时间点前移，及早暴露、识别并满足制约整个搜索过程中的瓶颈机床和关键工序赋值，以避免搜索后期出现约束冲突而导致已调度中间结果发生大面积回溯。

5 约束优化调度算法设计

遵循上述的两阶段调度和动态修订搜索空间的调度策略，结合“Thrashing”现象消减机制，在深度优先搜索算法的基础上，设计了图1所示的约束优化调度算法（constrained opti mization schedule al gorit h m，COSA）框架。其中，Un Sched为待调度工序集；Sched为已调度结果集；Op为各搜索状态下的变量排序启发结果（即关键工序）；St为Op的开工时间赋值。该算法的步骤如下：

（1）初始化。系统启动后，首先初始化待调度工序集Un Sched和已调度结果集Sched，并设置时间粒度、回溯阈值等系统参数。

（2）初始化工序开工时间窗。依据前述约束传播方法产生初始搜索状态下各工序开工时间的值域。

（3）搜索结束判定。检测Un Sched内有无剩余待调度工序，如果UnSched＝Ø，则整个搜索进程结束，算法最终求得调度解或证明调度问题无解，否则，则进入下一步。

（4）一致性预处理。遵循一致性预处理机制，采用文献［13］提出的动态一致性增强算法，依据上次搜索状态下的关键工序赋值（Op，St），结合工序路线和机床独占性2类硬约束对剩余搜索空间实施预修剪。

（5）约束冲突检测。检验上次搜索状态下的关键工序赋值（Op，St）与Sched内已调度中间结果有无约束冲突，若发生冲突，则进行顺序回溯处理［5］，若无冲突，则进入下一步。

（6）瓶颈机床识别。根据回溯前移机制，采用文献［14］提出的瓶颈机床动态识别方法：首先依据上述约束优化调度模型对剩余搜索空间的工序开工时间集进行提前／拖期成本计算，再进行当前搜索空间的概率计算，即依次计算各工序开工时间的主观概率、工序对机床的独立需求概率、机床累计需求概率之和，最后以累计需求概率之和最大的机床作为当前搜索状态下的瓶颈机床。

（7）单机排序优化。以步骤（6）的输出结果瓶颈机床作为输入参数，采用文献［14］提出的工序变量排序和赋值优化方法，输出当前搜索状态下的关键工序开工时间取值。① 工序变量优化排序：以竞争同一瓶颈机床的所有待调度工序作为排序对象，以工序对机床的独立需求概率值作为排序准则，在竞争高峰时段选择独立需求概率值最大的工序作为当前搜索状态下的变量排序输出结果Op。②关键工序赋值优化：以工序变量优化排序输出结果Op为输入，在Op剩余值域内选择调度成本最小的开工时间作为关键工序Op的最终赋值St。

（8）将关键工序赋值结果（Op，St）保存进Sched，同时从Un Sched中剔除工序Op，算法进入步骤（3），继续以上循环处理。

图1 约束优化调度算法

6 仿真试验

6．1 调度用例设计

随机生成80个调度问题，通过调整拖期系数τ、交货期分布R和瓶颈机床数量Nbtnk三个参数的不同组合产生8组调度问题（表3），每组调度问题包括10个调度子问题，每个调度子问题包含20个零件和5台机床，各零件均包含5道工序，且根据线性工艺路线依次经过5台机床，各工件经过机床的顺序随机产生。

表3 调度参数设置表

（1）拖期系数τ：用以调整各零件交货期的平均松弛度。各零件的平均交货期设定为（1－τ）M，其中，M ＝为 零件数量，Rbtnk为瓶颈机床为竞争机床Ri的所有工序的平均加工周期。

（2）交货期分布R：用以调节不同零件交货期的集中程度，各零件的交货期依据（1－τ）×M×U（1－R／2，1＋R／2）随机产生。R 值越小，表示各零件交货期分布越集中，调度难度更大。

（3）瓶颈机床数量Nbtnk：用来调节初始状态下调度任务集内的瓶颈机床数量。

6．2 参数设置和评价指标设计

6．2．1 加工参数设置

（1）零件批量Si依据U（1，7）等概率随机生成。

（2）工序加工周期duli按Si×U（0．5，1．5）等概率随机生成。

（3）零件拖期惩罚系数tar di按5U（1，2Si）等概率随机产生。

（4）库存成本系数invli：考虑到库存成本与零件批量、原材料价格等因素相关，在该试验中，将invli设置为零件批量Si，暂未考虑材料价格因素的影响。

（5）最早可接受释放期er di和最晚可接受的完工时间lcdi：为增加调度问题的复杂度，上述8组调度子问题内所有零件均设置为相同的最早可接受释放期er di＝0和最晚可接受完工时间lcdi＝2 M。

6．2．2 评价指标设计

选择包括上述约束优化调度模型中的调度总成本在内的4个评价指标来评估算法性能。其中，平均加权拖期用来评测调度拖期性能好坏；平均加权流动时间用以评测零件加工过程中的在制品库存成本；平均加权系统时间用来评测零件的成品库存成本和在制品库存成本。

（1）平均加权拖期成本。该评价指标是指各零件拖期成本的加权平均值，即

（2）平均加权流动时间。该评价指标是指各零件从开始加工至加工结束所需时间的加权平均值，用以评价在制品的流动库存成本，其表达式为

（3）平均加权系统时间。该评价指标包括零件因提前完工而产生的成品库存成本和在制品库存成本两部分，该指标综合反映了各零件库存成本和在制品库存成本，表达式为

6．3 仿真结果分析

文献［15］针对提前／拖期调度问题，提出了两种有效的Tardy／Early排序规则，即线性E／T排序（LIN－ET）规则和指数E／T排序（EXP－ET）规则，并通过试验证明这两种排序规则在降低提前／拖期成本方面具有优势。仿真试验环境为：CPU为Intel 2．4GHz，内存为1．98GB；仿真软件采用MATLAB 7．0。该试验以上述调度用例为测试对象，将本文提出的约束优化调度算法COSA和LIN－ET、EXP－ET两种规则进行比较。图2～图5分别表示COSA和LIN－ET、EXP－ET在平均调度总成本、平均加权拖期、平均加权流动时间和平均加权系统时间4个评价指标下的试验结果。

图2 平均调度总成本仿真结果

在仿真试验中，COSA在总共80次试验中，平均搜索效率（定义为待调度工序总数和求得调度解所产生的搜索状态数的比值）为85．6%，平均计算时间为35s。说明COSA能够有效降低“Thrashing”频发现象，从而保证搜索算法以较高的搜素效率和较小的计算成本求得E／T调度问题的优化解。

图3 平均加权拖期成本仿真结果

图4 平均加权流动时间仿真结果

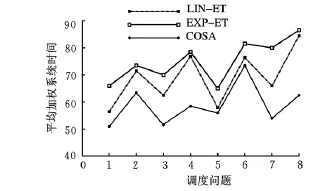
图5 平均加权系统时间仿真结果

从图2可以看出：COSA在总共8组试验中，除第7组试验外，其余7组试验得到的平均调度总成本均小于LIN－ET和EXP－ET。从图3可以看出：对于拖期成本指标而言，COSA和EXP－ET的性能基本相当，但要优于LIN－ET在拖期成本方面的表现。

从图4、图5可以得知：COSA在压缩在制品库存和成品库存两项指标上明显优于LIN－ET和EXP－ET。尤其在调度环境最为苛刻的第8组试验（瓶颈机床数量多，交货期松弛度紧，且各零件交货期分布较集中）中，当LIN－ET和EXP－ET的在制品库存成本和成品库存成本大幅攀升（达到峰值）的情况下，而COSA则维持在一个相对较低的库存水平。

与EXP－ET规则（该方法性能优于LINET）相比较而言，在共8组仿真试验中，COSA降低在制品流动库存成本15%～35%，降低成品和在制品库存总成本10%～30%，压缩平均调度总成本8%以上。

7 结束语

本文在满足工艺路线、机床能力和交货期约束条件的前提下，将提前／拖期成本指标引入调度问题，从而将约束满足求解JSSP的传统方式转化为约束优化求解；遵循解决实际工程问题的思维模式和原则，将复杂的调度优化问题划分为瓶颈机床优先识别和单机排序优化两个阶段，以降低大规模JSSP的计算复杂度和提高调度方法的实用性；为了降低回溯搜索中的“Thrashing”现象发生概率，引入一致性预处理机制以事先修剪和过滤剩余搜索空间的潜在冲突源，回溯前移机制可以有效避免搜索后期出现约束冲突而导致已调度中间结果发生大面积回溯的弊端。

为综合测试COSA算法性能，设计了一组交货期的松弛度和集中度可组合调整、加工参数随机产生的80个调度问题，并将COSA与在提前／拖期调度方面具有优势的LIN－ET、EXP－ET排序规则进行比较，结果表明：COSA与EXPET在拖期成本指标方面结果相近，但在减少在制品库存成本和成品库存成本两方面具有明显优势，从而保证了调度总成本相对较低。

［1］ Fox M S．Constraint－directed Search：A Case Study of Job－shop Scheduling［D］．Pittsbur gh：Car negie－Mellon University，1983．

［2］ Fox M S，Smith S F．ISIS－ a Knowledge－based System for Factor y Scheduling［J］．Expert Systems，1984，1（1）：25－49．

［3］ Smith S F，Peng Si Ow，Jean－Yves Porvin．OPIS：an Opportunistic Factory Scheduling System［C］／／Proceedings of the 3rd International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems．Charleston，1990：268－274．

［4］ Sadeh N，Fox M S．Variable and Value Ordering Heuristics f or t he Job Shop Scheduling Constraint Satisfaction Problem ［J］．Artificial Intelligence，1996，86（1）：1－41．

［5］ Sadeh N，Sycara K，Xiong Y．Backtracking Techniques for the Job Shop Scheduling Constraint Satisfaction Problem［J］．Artificial Intelligence，1995，76（1／2）：455－480．

［6］ Barták R，Skalicky T．A Local Approach to Automated Correction of Violated Precedence and Resource Constraints in Manually Altered Schedules［C］／／Proceedins of MISTA 2009：Fourth Multidisciplinary International Scheduling Conference：Theory and Applications．Dublin，Ireland，2009：507－517．

［7］ Barták R．Constraint Satisfaction Techniques in Planning and Scheduling：An Introduction［J］．In Archives of Control Sciences，2008，18（2）：141－158．

［8］ 郭冬芬，李铁克．基于约束满足的车间调度算法综述［J］，计算机集成制造系统，2007，13（1）：117－125．

［9］ 段黎明，陈进，刘飞．基于约束分析的Job Shop调度算法的综述［J］．重庆大学学报，1998，21（1）：133－138．

［10］ 陈恩红，薛瀚宏．基于约束满足的Job Shop调度问题求解方法研究［J］．软件学报，1998，9（12）：946－948．

［11］ 上官春霞，周泓，师瑞峰，等．作业车间排序重调度问题及其改进修复约束满足算法［J］．计算机集成制造系统，2008，14（9）：1742－1751．

［12］ Dechter R，Meiri I．Experimental Evaluation of Preprocessing Techniques in Constraint Satisfaction Problems［C］／／Proceedings of the Eleventh International Joint Conference on Artificial Intelligence．Detroit，1989：271－277．

［13］ 杨宏安，孙树栋，司书宾．基于动态一致性增强技术的Job Shop调度算法研究［J］，西北工业大学学报，2007，25（4）：523－527．

［14］ 杨宏安．基于COP的作业车间调度问题研究［D］．西安：西北工业大学，2007．

［15］ Peng S O，Morton T．The Single Machine Early／Tardy Problem［J］．Management Science，1989，35（2）：177－191．