超重型数控落地铣镗床滑枕挠曲变形补偿研究

吴凤和 王少伟 杨育林 王跃宏

1．燕山大学，秦皇岛，066004 2．齐齐哈尔二机床（集团）有限公司，齐齐哈尔，161005

0 引言

数控落地铣镗床是一种适用于大型零部件机械加工的通用机床，其最主要的结构特征一是采用立柱支承，二是由主轴箱和滑枕构成悬臂式运动部件。超重型数控落地铣镗床是指主轴直径不小于320 mm、滑枕行程不小于2000 mm、镗轴行程不小于1800 mm的落地铣镗床，目前只有德国、意大利、中国等少数国家掌握其设计制造核心技术，大行程滑枕的变形补偿问题是其主要技术难点之一。

文献［1］给出了一种分段补偿法，该方法在滑枕内部上半侧前后分别安装推杆和拉杆，虽然可以较好地补偿滑枕的角度摆动误差，但控制过程较难实现；文献［2］利用预应力挠曲加工方式实现挠度补偿，采用数控加工方法将滑枕的变形部分预先加工去除，使滑枕在工作伸出时处于平直状态，该方法能够产生一定的补偿效果，但对滑枕的加工与装配要求较高；文献［3］介绍了一种通过机床数控系统实现滑枕挠度补偿的方法，该方法利用数控系统自动检测滑枕挠度，通过控制Y轴上升相应的位移来实现补偿，但它仅补偿了滑枕的挠度，滑枕的弯曲变形并未考虑；文献［4］采用电液比例控制方式对滑枕低头进行补偿，虽然取得了一定的补偿效果，但是电液比例控制需要准确把握滑枕各个阶段的变形函数，对于快速运动的滑枕来说往往会出现很大的偏差；文献［5］采用液压重心偏心补偿法，在主轴箱前后端分别安装一个平衡锤以平衡因主轴箱重心变化导致的滑枕低头，该方法操作简单，但是因滑枕自身重力引起的滑枕低头没有彻底解决；文献［6－10］介绍的拉杆补偿法是一种常用的滑枕挠度补偿方法，该方法能够较好地解决因自重导致的滑枕挠曲变形，但补偿力的确定与精确加载是难点，通常采用实验方法确定补偿力，效率较低，调试周期较长，影响生产进度。

本文以TK6932数控落地铣镗床为例，研究超重型数控落地铣镗床滑枕挠曲变形及补偿问题，给出了一种数值计算与理论分析相结合的研究方法：利用有限元分析方法得到滑枕挠曲变形分布规律和变形与滑枕行程关系曲线；通过理论分析得出拉杆补偿法的补偿力初算公式，再结合有限元分析方法最终得到补偿力与滑枕行程关系曲线。

1 滑枕变形分析

滑枕在落地铣镗床中起到连接主轴箱和主轴的作用。TK6932超重型数控落地铣镗床滑枕的三维实体模型如图1所示，滑枕的整体外形为长方体，四面均为导轨面，内部安装铣轴和镗轴。

图1 滑枕三维实体模型

在自身及主轴等附件重力的作用下，滑枕在伸出过程中必定会产生挠曲变形。为分析其挠曲变形情况，采用三维CAD软件建立滑枕实体模型，导入到有限元分析软件进行静力分析，利用通用后处理器即可以直观地观察到滑枕的挠曲变形情况。

TK6932滑枕的总行程为2000 mm，以200 mm行程为间隔依次采点，可计算出滑枕在不同行程位置的挠曲变形量（表1）。图2为滑枕行程2000 mm时的Y向位移云图。

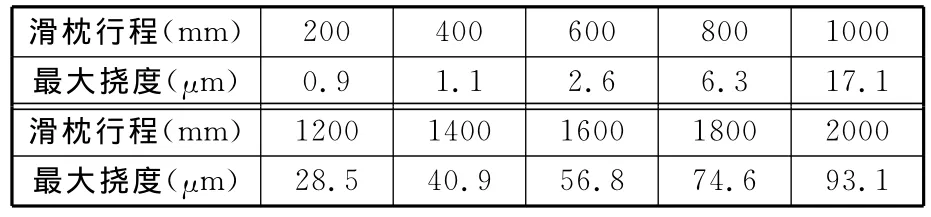
表1 滑枕各行程位置的最大挠度

图2 滑枕行程为2000mm时的Y向位移云图

对表1中的数据进行拟合处理可得到滑枕挠曲变形与滑枕行程关系曲线（图3中计算曲线）。

国家机械行业标准［11］规定，落地铣镗床滑枕的变形应满足0．02 mm／500 mm的精度要求，从分析结果可知，当滑枕行程为1000 mm时，其最大变形量为17．1μm，此变形量能够满足精度要求。由此可得出结论：滑枕的挠曲变形补偿只需在1000～2000 mm行程之间实施，而行程小于1000 mm时，不需要对其采取补偿措施。

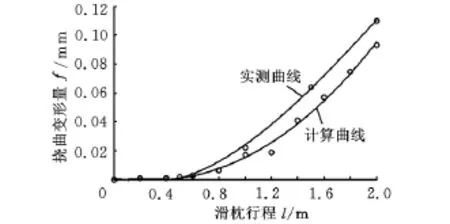
图3 滑枕挠度曲线对比

2 挠曲变形补偿措施

滑枕挠曲变形是受重力作用而引起的，因此补偿的基本思路就是：平衡掉导致变形的重力。可以施加一种外载荷产生与重力引起的弯曲变形大小相等且方向相反的变形，从而实现挠曲变形补偿。

基于上述原理，本文采用拉杆补偿法对挠曲变形进行补偿，具体措施是：在滑枕内部上方安装两个细长拉杆，拉杆的拉力由液压油缸提供，通过调整拉力来补偿滑枕的挠曲变形。拉杆及油缸的安装如图4所示。

图4 拉杆及油缸安装示意图

由滑枕挠曲变形与滑枕行程关系（图3中计算曲线）可知，滑枕行程小于1000 mm时，不需要对其采取补偿措施，因此，只需将拉杆的作用位置设计在距滑枕悬伸端端面距离小于1000 mm的适当位置即可。当滑枕行程小于拉杆作用点至滑枕悬伸端端面的距离时，拉杆将不会对滑枕挠曲产生补偿效果，这样也在一定程度上减小了滑枕总的补偿频率。另一方面，滑枕采用此种拉杆安装方式也为夹紧装置等附件提供了足够的安装空间。

3 拉杆补偿分析

3．1 理论分析

滑枕的挠曲变形是由于滑枕的自重、铣轴和镗轴及其他附件的重力因素而产生的弯曲变形。为分析方便，将滑枕结构近似为方截面等直梁结构，作用于滑枕的重力载荷可简化为均布载荷q；铣轴、镗轴及其附件对滑枕的作用力是通过与滑枕装配的组合轴承来实现传递的，第二组轴承距滑枕悬伸端端面的距离为2275 mm，而滑枕的最大行程为2000 mm，所以只考虑第一组轴承对滑枕变形产生的作用力F0，则滑枕的受力可简化为图5所示的情况。

图5 滑枕受力简图

采用拉杆补偿后，滑枕受力情况如图6所示。其中，F1和F2为拉杆拉力，产生偏心压缩的效果；q为作用于滑枕的均布载荷，使滑枕产生向下弯曲的效果；e为拉杆作用点在滑枕横截面上距滑枕中心线Z轴的距离；θ为拉杆中心线与滑枕中心线所构成的平面与中性层（水平）的夹角。

图6 滑枕拉杆补偿受力简图

为保证滑枕悬伸端端面挠度为零，则需拉杆产生的挠度与滑枕自重产生的挠度大小相等，即

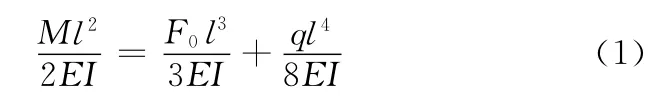
式中，M为两补偿拉杆拉力简化所得力矩之和；E为滑枕材料弹性模量：I为滑枕截面惯性矩。

由于两个拉杆上的补偿力相等，设F1＝F2＝F。由图5可知，补偿力F产生的力矩M 可表示为

拉杆位置确定后，θ也随之确定，根据滑枕的结构尺寸可算得e sinθ＝310 mm，该尺寸即为拉杆在竖直方向上与滑枕中性层的距离。滑枕行程l可通过数控系统检测得到。公式中其他参数均为已知量，q＝15k N／m，F0＝22．5k N（通过滑枕的力平衡方程计算得出）。

由式（1）简化可得

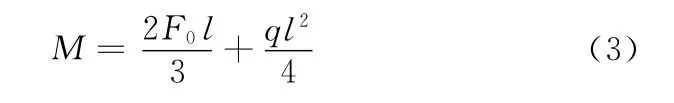
将式（2）代入式（3）得

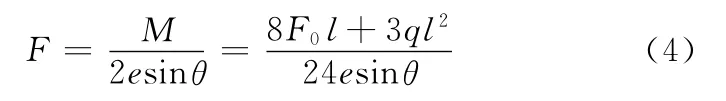
式（4）就是拉杆所需提供补偿力的初算公式。

当滑枕达到最大行程时，l＝2000 mm，将其他参数值代入式（4），可得滑枕行程为2000 mm时所需提供的补偿力F＝73k N。

同理，依据式（4）可计算出滑枕在1000～2000 mm中（间距为200 mm）5个不同行程位置拉杆应提供补偿力的初算值，如表2所示。

表2 滑枕不同行程位置拉杆补偿力的初算值

3．2 数值仿真

利用有限元软件对滑枕施加补偿力（初算值）后的变形情况进行分析，可得到滑枕补偿后滑枕的变形量。若变形量超过补偿精度要求，则根据分析结果对补偿力初算值进行修正，然后再进行有限元分析，直至变形满足补偿精度要求为止。

图7是滑枕行程为2000 mm时补偿后的变形云图，由云图可知滑枕悬伸端端面的Y向变形量为10μm，该变形满足0．02 mm／500 mm的精度要求，故不再需要对其进行修正。

图7 补偿后滑枕为2000 mm行程时的变形云图

利用上述方法得到的补偿力与滑枕行程关系曲线如图8所示。该曲线为实施滑枕挠曲变形自适应补偿提供了条件。

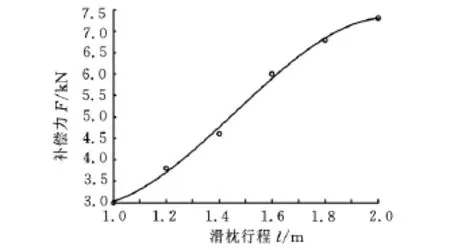
图8 补偿力与滑枕行程关系曲线

4 实验研究

4．1 滑枕挠曲变形测量实验

TK6932超重型落地铣镗床的滑枕变形不仅包括滑枕、镗轴等零部件自重引起的挠曲变形，还包括立柱变形、主轴箱低头、滑枕低头等因素导致的变形，在测量时必须去除其他因素引起的滑枕变形。为此采取如下的测量方法：

（1）将千分表固定在滑枕的前端面，测量滑枕伸出某一行程位置时的变形量f1（包括挠曲变形、主轴箱低头、滑枕低头等因素引起的滑枕变形）。

（2）将千分表固定在测量平台上，测量杆位于主轴箱前端面位置，而测量头与滑枕根部下端面接触，在滑枕的同一行程位置测量由立柱变形、主轴箱低头、滑枕低头等因素引起的变形量f2。

（3）将两次测得的变形量相减，得到由滑枕、镗轴等零部件自重引起的挠曲变形量f，即f＝f1－f2。

重复上述步骤，可得到滑枕在不同行程位置的最大挠曲变形量，经拟合得到滑枕挠曲变形实测曲线（图3中实测曲线）。

由图3可知，滑枕挠曲变形实测值（实测曲线）与计算值（计算曲线）相比，从曲线变化趋势和形状看，计算曲线与实测曲线基本一致，两者只存在较小的偏差（最大差值小于0．02 mm），说明本文方法得到的滑枕挠曲变形计算结果可信度较高。存在偏差的主要原因是悬臂部件各零件间存在装配间隙。

4．2 滑枕挠曲变形补偿实验

根据上述补偿力与滑枕行程关系曲线，对拉杆施加相应的补偿力，进行滑枕挠曲变形补偿实验。采用与滑枕挠曲变形测量实验相同的测量方法对挠曲变形量进行测量。理论上，补偿后挠曲变形量为零，但实际拉杆存在补偿精度问题，只要保证挠曲变形满足机床精度要求即可。

具体实验步骤如下：

（1）依据补偿力与滑枕行程间的关系曲线确定滑枕行程分别为1000 mm、1500 mm、2000 mm的拉杆补偿力，并将其施加到滑枕上。

（2）用千分表测量滑枕在上述行程位置的变形量f1和变形量f2（f1和f2的具体测量方法同4．1节）。

（3）求得滑枕在同一行程下的两次变形量之差，即为补偿后滑枕的挠曲变形量f＝f1－f2。

实验结果如表3所示。

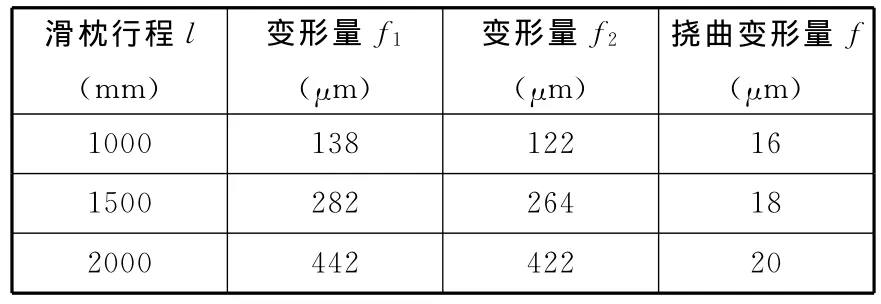
表3 滑枕挠曲变形量实验数据

由实验数据可知，补偿后滑枕的挠曲变形量最大值为0．02 mm，满足0．02 mm／500 mm的机床精度要求，说明本文给出的拉杆补偿力与滑枕行程间的关系曲线与实际吻合较好，可信度较高，可用于滑枕挠曲变形补偿。补偿后，存在较小挠曲变形的主要原因是有限元分析过程中忽略了装配间隙等误差影响因素。

5 结论

（1）通过有限元分析方法得到了超重型数控落地铣镗床滑枕挠曲变形与滑枕行程关系曲线，实验表明，挠曲变形计算曲线与实测曲线偏差较小，趋势一致，可较好地预测超重型落地铣镗床滑枕挠曲变形情况。

（2）通过理论分析给出了拉杆补偿的补偿力初算公式，结合有限元分析方法得到了补偿力与滑枕行程关系曲线，实验数据表明，依据该曲线进行滑枕挠曲变形补偿可满足机床精度要求。

（3）数值计算与理论分析相结合的研究方法较好地解决了超重型数控落地铣镗床滑枕挠曲变形补偿难题，减少了调试阶段大量的实验工作，提高了产品开发效率，对高档数控机床的变形分析及补偿研究具有参考价值。

［1］ 孙德洲．滑枕下垂变形的分段补偿方法［J］．组合机床与自动化加工技术，2008，50（6）：77－83．

［2］ 戴晨，刘小鹏，张文桥．TK6916B数控落地铣镗床补偿系统分析［J］．湖北工业大学学报，2007，22（4）：4－5．

［3］ 张文国，包杰．用PC软件实现滑枕低头的自动补偿［J］．一重技术，1998，37（1）：1－5．

［4］ Rah man Mahbubur，Heikkala Jouko，Lappalainen Kauko．Modeling Measurement and Error Compensation of Multi－axis Machine Tools［J］．Inter national Journal of Machine Tools and Manufacture，2000，40（10）：1535－1546．

［5］ 张伯鹏，张年松．机床横梁重力变位的自演进补偿［J］．清华大学学报，2006，46（2）：191－193．

［6］ 王洪才．数控铣镗床滑枕下垂补偿系统［J］．制造技术与机床，2003，53（6）：24－25．

［7］ 蔡有杰，陆义南．大型铣镗床主轴滑枕变形分析与改进［J］．机械设计与制造，2008，46（3）：127－128．

［8］ 王建中，黄成军．大型落地铣镗床方滑枕精度变形补偿［J］．制造技术与机床，2006，56（7）：61－62．

［9］ 刘文志．数控卧式铣床滑枕变形有限元分析及补偿［J］．现代制造工程，2008，30（1）：56－58．

［10］ Bert R．Jorgensen，Yung C Shin．Dynamics of Spindle－bearing Systems at High Speed Including Cutting Load Effects［J］．Jour nal of Manufacturing Science and Engineering，1998，120（5）：387－394．

［11］ 机械行业国家标准，JB／T8490．1－96．数控落地铣镗床、落地铣镗加工中心精度检验［S］．北京：中华人民共和国机械工业部，1997．