板式塔弓形降液管液相流场CFD数值模拟
2010-05-28黄雪雷李育敏
黄雪雷,李育敏
(浙江工业大学化学工程与材料学院,浙江 杭州 310032)
降液管作为板式塔塔板间液体传输的通道,在传输过程中实现气液两相分离,同时为塔板入口的液体提供初始分布.因此,降液管的性能直接影响整个板式塔的分离效果.降液管存在多种结构形式,在工业上应用最为广泛的是弓形降液管[1].众多研究者对弓形降液管内的表观液速、停留时间、清液层高度、泡沫层高度等流体力学特性进行了深入研究,提出设计准则,但大都停留在定性分析和依据个人试验数据上[2-3],在实际设计应用中往往不尽合理.
近年来,随着分离技术不断发展,这种凭经验的宏观设计方式的局限性也越来越明显,这要求我们获得降液管内部详细的流场信息.新型的计算流体力学(Computational fluid dynamics,CFD)技术被应用到降液管的研究中.使用计算流体力学FLUENT软件,采用标准k-ε湍流模型及SIMPLEC算法[4]模拟计算降液管底部的液相流场.为验证模拟结果的正确性,采用热膜风速仪对降液管底部液相流场进行详细测量,将实验测量结果与模拟结果进行比较.
1 计算模型和数值方法
1.1 计算模型
建立的降液管模型结构类似柱体,而且并不复杂,可近似看作管内流动,因此选用标准k-ε湍流模型作为湍流方程进行封闭,可以满足湍流计算的准确性.方程求解的方法采用SIMPLEC算法.
模拟计算的入口边界条件:入口处,液相速度均匀分布,且垂直入口截面,进口速度与试验测量值一致,取0.018 m/s.液相湍动能与湍流密度计算式分别为

1.2 数值方法
采用了六面体和棱柱体相结合的网格划分单元[4]对降液管模型进行网格划分.GAMBIT将降液管作为包含两个端面和一个柱体构成的逻辑圆柱体来处理.作为这些圆柱体端面的面被称为源面.GAMBIT从这两个源面开始进行网格划分,最终扩展到整个计算区域.降液管模型堰长取800 mm , 宽度取150 mm,降液管底隙高度取20 mm,模型高度取降液管内清液层高度为80 mm.根据降液管的物理模型及网格划分情况,网格总数为104 000个.
模拟计算的出口边界条件:在出口边界,取充分发展的管流条件,即出口方向的各个流动变量的扩散通量为0.由于降液管出口压降及速度未知,故取出流边界条件.
模拟计算的底面与边壁边界条件:设置降液管底面与边壁为无滑脱的壁面条件.在板上各个方向速度为零.采用壁面函数法,其基本思想是使用半经验公式将近壁区内的物理量与湍流核心区内某点待求的未知量直接联系起来.这样既可以节省计算时间,又可以计入壁面粗糙度的影响.
2 实 验
本实验流程如图1所示,试验在直径为1 200 mm的有机玻璃塔进行,塔内安装3块弓形降液管筛板,中间塔板的降液管为测试降液管.板间距600 mm,堰高50 mm,堰长和降液管底隙高度与模拟设定相同,即分别为800 mm和20 mm.
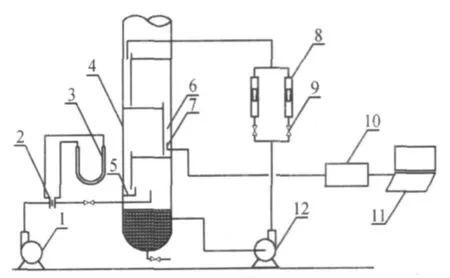
图1 实验流程装置图Fig.1 Scheme of experimental setup
试验物系为空气—水,空气由风机经孔板流量计从塔下部进入塔内,经过最下层塔板分布均匀后,进入试验塔板.水由离心泵经转子流量计后至第一块塔板,经过分布后进入试验降液管.笔者考察降液管底部的流场分布,过大的气液量,会导致降液管内混合剧烈,清液层不明显.在调试后采用以下试验条件:液体流量L=4.95 m3/h和8.0 m3/h,气相动能因子F=0.72 m/s(kg/m3)0.5和 1.24 m/s·(kg/m3)0.5,对降液管清液区中不同平面上的液体速度分布进行测量.
采用Dantec公司生产的StreamLine CTA系统热膜风速仪测量降液管下方的液相流场分布.数据采集和处理由Stream Line软件处理.流场分布以中心截面对称,故在降液管弧形塔壁处一侧开12个孔用以安装热膜风速仪测试探头,如图2.所开孔用橡胶塞密封,探头穿过橡胶塞,迎着液流方向.

图2 试验降液管的测试探头安装孔分布图Fig.2 Scheme of orifices on test downcomer
测试点沿降液管堰长方向、降液管宽度方向和高度方向均布,共42个测试点.
3 模拟分析
3.1 初步分析
FLUENT软件模拟得到弓形降液管的三维液相速度矢量分布图,图中箭头所指方向即为速度矢量方向,如图3所示.由图可以看出,速度从入口开始逐渐增大.

图3 弓形降液管的三维液相速度矢量分布图Fig.3 Distribution of velocity vector of downcomer
分析沿堰长方向平面内的速度分布.在距堰壁38 mm处平面内,中间位置的速度比两侧位置的速度小18.9%~20.8%;并且中间位置的速度方向垂直向下,两侧位置的速度方向斜向下指向两侧,这是由于弓形降液管中间宽大两侧狭小的形状造成的.因此,在降液管下方,液体沿堰长方向流动不均匀.
沿降液管宽度方向平面内的速度分布.靠近塔壁处的液体速度沿从上往下的高度方向逐渐减小,而靠近堰壁处液流速度逐渐增大.在同一高度处,液体速度沿从近塔壁处到近堰壁处方向逐渐增大,速度矢量方向与垂直方向的夹角也逐渐增大,如图4所示.在同一高度处,距堰壁38 mm处的平均液流速度比距堰壁76 mm处的平均液流速度大6.4%~37.8%.

图4 沿降液管宽度方向平面内的速度分布Fig.4 Distribution of velocity vector along plane of width direction of downcomer
3.2 降液管底部拐角处存在的缓流区
弓形降液管内液体折转90°后由底隙流出.从图4可见,近塔壁拐角处存在缓流区.将图4中圈出的区域放大后,如图5所示,可以明显发现在此拐角处存在漩涡.由于漩涡存在,导致此处液流缓慢,甚至形成液体流动死角.若处理的物系带有杂质颗粒、粘性较大或者容易形成聚合物,那么这些杂质将在这些流动死角形成区域沉淀.这些沉淀若不及时清除,就会逐渐填充在降液管底部空间,甚至堵塞降液管底隙.因而我们在实际工程设计中尽量避免这种情况发生.

图5 区域放大图Fig.5 Local amplification
3.3 模拟与实验数值的比较
通过模拟计算和试验测量比较,我们发现两者总体趋势是一致的,两者对比结果见图6.
图6(a)中的数据最大相对误差为30.08%,最小相对误差为0.09%,平均相对误差为12.96%;图6(b)中的数据最大相对误差为23.37%,最小相对误差为0.72%,平均相对误差为7.20%.
我们还发现在降液管最底部,模拟速度矢量方向与垂直方向的夹角偏大.这是因为在单相模拟程中,并没有计入气相的影响,而且模拟计算所采用的模型在边界条件的处理上较为简单.
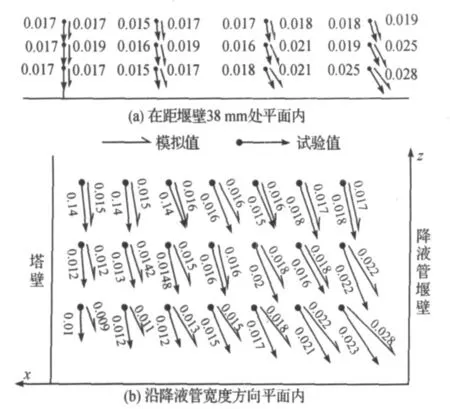
图6 模拟和实验速度比较图Fig.6 Comparison between calculated and measured velocity
4 结 论
针对降液管给出模型方程计算所需要的各种边界条件及其计算网格,运用计算流体力学软件,选用标准k-ε湍流模型及欧拉两相流模型,模拟获得降液管三维液相速度场.沿堰长方向,中间位置的速度比两侧位置的速度小18.9%~35.7%.沿降液管宽度方向,靠近塔壁处的液体速度沿从上往下的高度方向逐渐减小,而靠近堰壁处液体速度逐渐增大.在同一高度处,液体速度沿从塔壁到堰壁方向逐渐增大.降液管底部近塔壁处存在漩涡和缓流区.在处理不洁物系或粘性较大物系过程中,该缓流区易形成杂质沉积,最终导致降液管堵塞.将计算流体力学的模拟速度值与实验速度值进行比较,发现两者吻合较好,最小相对误差只有0.09%,最大平均相对误差不超过15%.
[1] KISTER H Z.Distillation operation[M].New York:McGraw-Hill Publishing Company,1990.
[2] KIST ER H Z.Downcomer design for distillation tray columns[J].Chem Eng,1980,87(24):55-60.
[3] CHASE J D.Sieve-tray desigh part 1[J].Chemical Engineering,1967,31(6):105-116.
[4] PAT ANKAR S V.Numerical heat transfer and fluid fow[M].Washington:Hemisphere Publishing Company,1980.
