梁拱组合桥梁上部结构空间分析计算研究
2010-05-28施颖,史杰
施 颖,史 杰
(浙江工业大学建筑工程学院,浙江 杭州 310032)
随着社会发展,各种较复杂的桥型更多的应用到现代桥梁的建设中.这就须要应用大型空间分析程序对其进行内力分析.利用梁格理论对桥梁进行简化分析,既可满足一定的精度要求,提高计算效率,又方便与现行规范的配合应用,是一种目前较理想的计算方法[1-2].目前,梁格多应用在桥面梁等弯剪构件中,而在压弯构件中的应用则不多.结合某工程施工图设计在应用MIDAS/Civil 2006程序对其进行空间内力分析校验时,对该桥的模型作了一些有益的简化处理,不仅桥面梁以梁格简化处理,且该桥的压弯构件也以梁格模拟.同时建立对比模型,以校核简化模型的内力计算结果.
1 工程概况
该桥为某城市主干道上一座跨河桥,主桥为三跨预应力混凝土梁拱组合结构,跨径组合为35 m+60 m+35 m.上部结构桥面梁为变高度箱梁,梁中线处高度为1.80~3.64 m,截面形式为单箱多室截面,拱肋采用单箱多室截面,肋高为1.30 m;下部结构为实体墩身、承台桩基基础.桥梁横向分为三幅设计,中间一幅为机动车道桥,左右各一幅为非机动车和人行桥,桥面全宽为36.0 m.对中幅机动车道桥进行建模分析.该幅桥面宽度为17.5 m,按双向四车道设计,荷载标准为公路-I级,桥梁设计安全等级为一级,抗震按6°设防,抗震类别为B类.图 1为该桥主桥立面图.

图1 桥梁立面图(单位:m)Fig.1 The bridge elevation
2 梁格划分与模型建立
用梁格法模拟箱梁结构时,假定梁格网格在上部结构弯曲主轴平面内,纵向构件的位置均与纵向腹板相重合,这种布置可使腹板剪力直接由横截面上同一点的梁格剪力来表示[1].而纵向梁格的划分,以保证各梁格的中性轴一致为原则,一般将各箱室腹板之间切开,形成不等宽翼缘的工字形梁.对超静定结构进行作用(或荷载)效应分析时,箱形截面梁的翼缘宽度可取实际全宽[3],因此该桥计算取用箱梁翼缘全宽.本桥主梁为变高度箱形梁,在划分截面时,经试算比较保证各梁格截面中性轴误差约在±2%以内.拱肋箱梁为无翼缘等高度截面箱梁,只要保证工字形截面顶底板翼缘等宽,即可满足各纵向梁格中性轴位于同一直线上.
桥面梁中共设有13道厚度不等的横隔板,拱肋梁中每半拱肋各有1片横隔板.若横隔板间距较大,则必须增设横向虚拟梁,其间距一般为反弯点之间距离的1/4[1].MIDAS/Civil相关参考资料[4]建议以1.5 m左右一个横向联系梁在精度上一般可满足设计要求.同时考虑截面的变化点,将桥面箱梁的虚拟横梁间距取为1.0~1.2 m,而拱肋梁格线型曲率较大,虚拟梁间距一般取为0.5~1.0 m.横隔板位置的横向联系梁以实际横隔板截面建立,其余部位的虚拟横梁,则参考箱梁顶底板,以“二”字形截面计算.
拱座墩柱和V型斜撑均为实体混凝土,一般以实体单元或板单元建立是比较合理的.但考虑到MIDAS/Civil中各种单元的特征,以及与现行规范相配合,并根据结构受力特征及整体受力检算为目的,建模时均采用梁格代替.斜撑梁格参考拱肋建立,而拱座及墩柱简化为竖向短柱.因拱座及其墩柱截面尺寸较大,横向刚度可视为无穷大,设为一般截面刚度的106~108倍.斜撑或拱肋梁与拱座短柱的连接,应根据其实际连接特性,设置相应的刚性域.
整个桥梁的梁格划分,实质上是将整座桥梁沿纵向划分为若干片,而后根据梁格之间横向连接刚度,施以相应的横向连接.图2示出了部分截面划分情况.图3为桥梁模型网格划分示意图.简化模型全桥共使用梁单元3 848个.

梁格法应用于弯剪构件(如桥面梁),理论和实践上都比较成熟;而在压弯构件(如斜撑板)上应用较少.偏压构件以梁格简化计算时,会引起偏压构件本身及其他构件内力变化.因此建立的对比模型中,桥面梁、拱肋梁仍采用梁单元,而拱座墩柱改用实体单元,斜撑改用板单元.对比模型全桥共使用梁单元4 270个、板单元1 520个,实体单元4 800个.
由于仅是对该桥的上部结构(含拱座墩柱)的分析,并未对下部结构建模.因此对边界条件作如下假定:边支座为完全刚性的滑动支撑;拱座墩柱底为弹性支撑,共设11个节点弹性支撑,编号详见图2,变形时拱座底保持平截面.
3 计算结果分析
利用MIDAS/Civil2006程序分别建立以上两种模型进行计算,并对支座反力、结构内力或应力、桥梁基频和振型等方面的计算结果进行比较分析.
3.1 桥面梁、拱肋梁内力及支反力比较
两种模型在自重和移动荷载作用下各支反力误差均不超过1.5%;桥面梁内力误差一般不超过5%;拱肋梁轴力误差一般不超过3%,其弯矩和剪力误差一般不超过10%.表1为拱座墩柱底部分支反力结果对比,MVmax(MVmin)为移动荷载最大(小)作用效应;图4,5为1/2桥面梁Q2弯矩对比图(JM为简化模型,DM为对比模型);表2为边跨拱肋梁L2最不利位置内力对比表.梁Q2,L2及其最不利点位置见图2.
由以上结果对比分析可知,两种模型的桥面梁、拱肋梁内力及支反力计算结果符合较好,但桥面梁、拱肋梁也存在个别位置的个别内力误差较大,但误差较大点一般出现在内力反弯点或相应内力绝对值较小处,对于结构设计,这些位置均不是截面控制点.

表1 模型拱座墩柱底支反力对比表Table 1 The comparison of the support reaction

表2 拱肋梁L2内力对比表Table 2 The comparison of L2′s internal force

3.2 V型斜撑与拱座墩柱内力比较
对比模型中V型斜撑与拱座墩柱分别采用厚板单元、实体单元,根据程序特点,可提取计算相应截面在自重作用下的内力值,与简化模型比较.斜撑受力以压弯为主,在恒载作用下全截面轴力误差不超过1.1%,弯矩与剪力误差较大,一般不超过15%.V型斜撑上部与桥面梁格联接的模拟,在两个模型中很难一致;同时V型斜撑较短,内力分布受边界条件影响较大,斜撑内力误差偏大.简化模型各个斜撑柱与对比模型相应板单元内力值比较,则误差更大.表3所示为中跨侧斜撑最不利点(见图2)全断面内力比较.
移动荷载作用下,对比模型斜撑板可提取板单元节点应力值;简化模型可提取斜撑柱截面四个角点的应力.表4即为在移动荷载作用下截面D在移动荷载作用下截面正应力比较,两模型间误差一般不超过10%,表 4中应力以压为负,拉为正,位置Ⅰ-Ⅵ见图6中.

表3 V型斜撑截面内力比较表Table 3 The comparison of the V-bracing beam's internal force

表4 V型斜撑截面D在移动荷载作用下正截面应力比较Table 4 The comparison of the V-bracing beam feature point D's normal stress under moving load

图6 特征位置D断面图
同样可得到墩柱截面G在简化模型与对比模型中相应位置的内力比较结果,如表5所示.结果符合较好,但边支柱剪力误差稍大,可能与简化模型中边柱生成于外侧有关.简化模型中共设的11根墩柱,由外侧向中间对称编号为1-6.

表5 墩柱截面G内力比较Table 5 The comparison of feature point G's internal force
图7为对比模型截面G在移动荷载作用下最大(最小)正截面应力图,应力以压为负,拉为正.提取简化模型中墩柱截面应力:边跨侧,最大最小应力分别为0.26 MPa,-0.28 MPa;中跨侧,最大最小应力分别为 0.21 MPa,-0.36 MPa,与图7相比可知,简化模型最大截面正应力与对比模型符合较好,但简化模型最小截面正应力绝对值偏大.

图7 墩柱截面G在移动荷载作用下截面最大、最小正应力迹线图Fig.7 The normal stress graph of feature point G under MVmaxand MVmin
3.3 竖向自振频率比较
桥梁移动荷载分析时,必然要考虑到冲击系数的影响.参照规范条文说明[5]冲击系数一般应由桥梁的第一、第二阶竖向振动基频计算得出.表6为两种模型竖向基频对比情况,图8,9分别为两模型第一、第二阶竖向振型.比较可知,二者的基频几乎相等,振型形状完全一致,符合的较好.
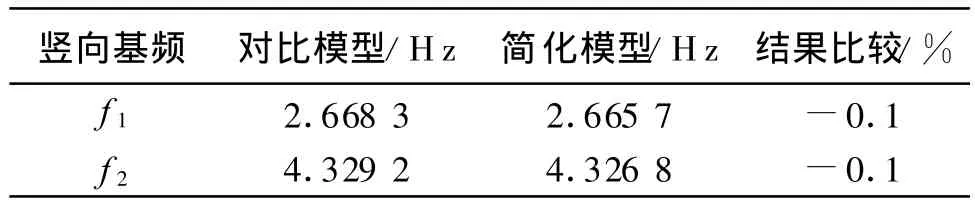
表6 竖向基频比较T able 6 The comparison of the vertical fundamental frequency

4 结束语
通过上面的对比分析,可以得出以下结论:采用梁格法进行内力分析时,横向联系梁的模拟至关重要,不同结构位置的横向联系梁应取用不同刚度,并要根据实际桥梁横向联系刚度来确定;梁格法不仅适用于受弯结构,对于类似拱座墩柱、V型斜撑等弯压结构,也可根据其受力特点,划分梁格来进行计算,并可得到较高的精度;弯压构件划成柱格后,若构件较短,则边界条件对其内力或应力分布影响较大,但是作为整体受力分析时,其计算精度还是可以接受的;梁格法建模型分析,仅使用梁单元而不使用实体或板单元,可明显减少单元数量和种类,减少机时,提高计算效率,而计算精度也能保证.
[1] 戴公连,李建德.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社,2001.
[2] HAMBLY E C.桥梁上部构造性能[M].郭文辉,译.北京:人民交通出版社,1982.
[3] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.
[4] MIDAS IT.梁格法建模注意事项[EB/O L].[2009-12-10].http://cn.midasuser.com/t_support/web_note/files/Grid%20model.pdf.
[5] 中华人民共和国交通部.JTG D60—2004 公路桥涵设计通用规范[S].北京:人民交通出版社,2004.
