再保险策略下的理赔总额近似分布研究
2010-05-22李凯
李 凯
(中央财经大学 中国精算研究院,北京 100081)
0 引言
在短期聚合风险模型中,所有的保单被视为一个整体,考虑在未来一段时期(如1年)内所发生的损失(理赔)总额。以每一次损失为基本对象,损失总额就是所有单个损失额的和。我们用S来表示损失总额,则有:

其中,Xi表示第i次的损失额,N表示损失次数,Xi和N都是随机变量,且相互独立。在聚合风险模型中,通常把S的分布称作复合分布,譬如当损失次数分布为泊松分布时,相应的复合分布被称作复合泊松分布。S的分布函数通常比较复杂,获得S分布的方法有卷积法、矩母函数法、递归法、傅里叶法等[1],但这些方法计算量非常大,且条件较强,所以我们常常采用近似分布来估计S的分布[2]。近似方法大致可分为两类:一类是给定分布函数类型(如伽马分布、对数正态分布),再采用矩估计确定参数,另一类则是对S进行调整,使其服从较为简单的分布(如正态功效近似)。由于理赔总额分布(如复合泊松分布)往往具有厚尾的性质,其偏度系数也显著大于0,故本文将采用平移伽马分布近似来估计再保险双方理赔总额的边际分布。
连接函数(Copula)理论在随机变量联合分布的估计问题中应用广泛[3][4][5]。首先,由于不限制边际分布的选择,可运用连接函数理论构造灵活的多元分布;其次,运用连接函数理论建模时,可将随机变量的边际分布和它们之间的相关结构分开研究,使问题大大简化。相关性分析中常用的连接函数主要有两大类:椭球类连接函数和阿基米德类连接函数。椭球类连接函数一般被定义为椭球类分布的连接函数,包括高斯连接函数、学生t连接函数和柯西连接函数。本文将重点应用高斯连接函数(正态连接函数)和学生t连接函数来刻画原保险公司和再保险公司理赔总额的相关性。
再保险优化问题中,有许多种目标函数可作为优化准则,如破产概率、效用函数等[6][7]。而将原保险公司和再保险公司相结合进行讨论亦颇具意义,双方均希望获得更多的保费并承担较低的风险,最优再保险策略应兼顾这两方面的关系,最直观的方法便是以联合生存函数作为优化准则,寻求联合生存概率最大的再保险安排。本文的主要贡献是找到了一种近似联合分布的有效方法,并将其应用于新的再保险优化准则,从而对再保险合同的决策提供有力依据。
1 理赔总额边际分布的近似
本文所讨论的再保险形式是:双方按比例a分摊保险责任,同时确定责任限额M,若原保险人理赔超过此限额,则剩余部分全部由再保险人承担。如发生赔付X,则原保险人与再保险人所承担的赔付分别为:
XI=min(aX,M),XR=X-min(aM,M)
特别的,当a=1时,该再保险形式为停止损失再保险;当M/a→∞时,为成数再保险。我们称之为复合型再保险。
聚合风险模型是将所有的保单视为一个整体,考虑未来一段时期内所发生的理赔总额(累积损失)。本节研究在一定的再保险合同下,原保险人与再保险人理赔总额的边际分布问题。对于具有同质风险的一类保单而言,若一次事件赔款金额为X,原保险人和再保险人分别承担XI,XR,则在一段时期内(通常为一年)原保险人和再保险人的理赔总额为:
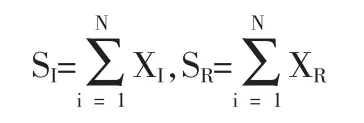
其中N为随机变量。(SI,SR)的联合分布函数为:
F(x1,x2)=Pr(SI≤x1,SR≤x2)
关于理赔总额变量S分布函数的近似问题,前人已经做了大量工作。我们希望获得SI,SR的联合分布,首先须寻求近似SI,SR边际分布的最佳方法。S的分布大多是右偏的,且有一个众数,这与伽马分布类似。假设随机变量X服从参数为(α,δ)的伽马分布,即具有下述分布函数:
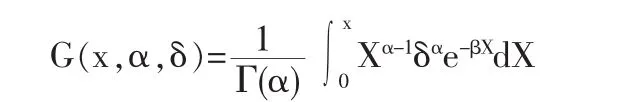
将它平移k后,即可得到平移伽马分布。显然,平移伽马分布具有三个参数(α,δ,k),如果用平移伽马分布近似理赔总额S的分布,就需要估计这三个参数的取值,可以用矩估计法进行估计。为了使平移伽马分布和S的前三阶矩相等,α,δ,k必须满足下述等式:
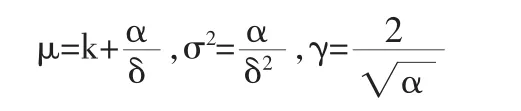
不难看出,形状参数a反映了分布的偏度,a取值越小则偏度系数越大。
2 理赔总额联合分布的近似方法研究
本文研究的核心内容是原保险人与再保险人的联合生存概率,我们将运用Copula函数(连接函数)描述原保险人和再保险人理赔总额之间的相关性。连接函数是将多个随机变量的联合分布函数用它们各自的边缘分布表示的函数,上一节我们给出原保险人和再保险人理赔总额的边际分布的最佳近似方法,再通过构造连接函数,便可获得二者理赔总额联合分布的近似解。本节首先将介绍连接函数的定义、性质和种类。而后,分别将椭圆连接函数、学生t连接函数应用于联合分布近似,同时进行随机模拟,寻求最有效、最准确的连接函数。
2.1 高斯连接函数
这种连接函数产生于一个具有线性相关矩阵Σ的多元正态分布:
C(u1,…,un)=H(Φ-1(u1,…,Φ-1un))
其中H是一个标准正态随机变量的联合分布函数

式中Φ-1(·)是一个标准正态分布的反函数,高斯连接函数具有零尾部相依性。
2.2 学生t连接函数
这个联接函数由一个多变量学生t分布产生,具有线性相关系数矩阵Σ:
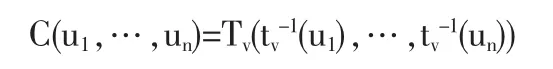
其中Tv是一个标准学生t向量的联合分布,自由度为v,
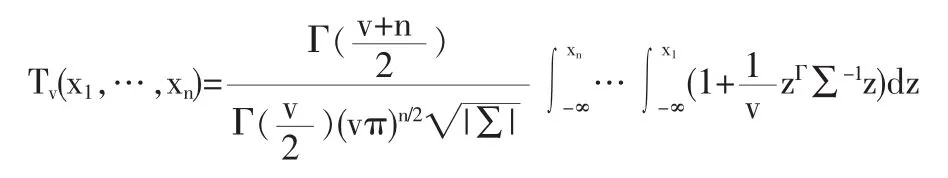
与高斯连接函数不同,学生t连接函数具有非零的尾部相依。
学生t连接函数主要依赖于自由度参数,Glasserman等人 (2002)认为强尾部相依性的自由度在3和7之间,而Demarta和McNeil(2005)认为在3和8之间。根据Embrechts等人(2002)可知,尾部独立的自由度(高斯连接函数)。因此,本文选择的连接函数,根据尾部相依性增加,我们预期依次是高斯、学生t(v=10)、学生t(v=5)连接函数。尾部越重的相依性连接函数在理赔总额分布中产生越厚的尾部。这就可以解释在厚尾相依性下,极端损失同时出现于原保险人与再保险人的情况更为频繁。
我们依次选择高斯、学生t(v=10)、学生t(v=5)连接函数,确定再保险双方理赔总额的关联结构。同时,我们仍然用模拟的方法取得联合分布概率,比较后得到最佳的连接函数。
3 基于联合生存概率的最优再保险的策略
从实务的角度来说,再保险合同的签订需兼顾到偿付能力、期望收益等因素,并符合再保险业务的监管规定。首先,双方的偿付能力对再保险合同有着较大的影响,若原保险人选择偿付能力充足的再保险公司进行投保,那么便可将大规模的风险分出,反之,原保险人须谨慎考虑分保安排。假设原保险人和再保险人的初始余额(准备金)分别为UI,UR,则基于联合生存概率的优化准则为:
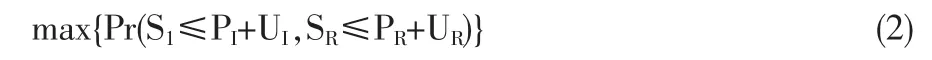
本节将通过一系列具体的例子确定复合型再保险的最优形式。之前讨论的例子均为复合泊松分布,且理赔额服从帕累托分布(重尾),本节的将进一步讨论复合二项、复合负二项分布,以及理赔额服从指数分布(轻尾)时的情形。
指数分布 若理赔额X服从期望为100的指数分布,即f(X=x)=1/ue-x/u,u=100。损失次数N分别服从均值为100的泊松分布(λ=100)、二项分布(n=200,q=0.5)、负二项分布(r=100,β=0.5)。考虑复合型再保险合同,a,M在集合Ω上取值。
Ω={(a,M)|a∈(0,1],M∈R+}
保费原则遵循期望保费原理,原保险人的附加因子θI=0.1,再保险人的附加因子θR=0.2,则再保险人获得保费:
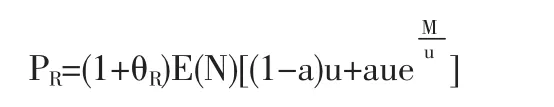
扣除再保险费后,原保险人剩余保费为:
PI=(1+θR)E(N)u-PR
依定义,还可求得原保险人与再保险人理赔总额的前三阶矩以及相关系数。设原保险人的初始余额(准备金)为UI=500,并选择实力较强、偿付能力充足的再保险人,其初始余额为UR=2000。
运用 Matlab 软件,分别取 a=0.01,0.02,…,1,M=10,20,…,2000,对于每一组(a,M),均可通过“Gamma-t Copula”方法求得联合生存概率的近似值,再取其最大值,便可得到该准则下的最优再保险策略。结果见表1。
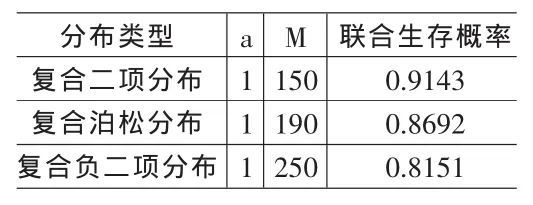
表1 准则1下的最优再保险策略
从结果看,当a=1,即超额赔款再保险时可达到最优。同时,我们选择同期望的理赔次数分布,方差(变异系数)从小到大依次为复合二项分布、复合泊松分布、复合负二项分布,而理赔总额方差的顺序也如此。比较这三种情形下的最优再保险策略,不难发现,联合生存概率差异较大,会随着理赔总额方差的增大而减小,这个结果是很容易解释的,因为损失期望相等时,方差越大则对于原保险人和再保险人来说,承担的风险就越大,故联合生存概率会变小。

表2 准则1下的最优再保险策略
帕累托分布 若理赔额X服从期望为100的帕累托分布,即 f(X=x)=αkα/(k+x)1+α,其中 k=400,α=5 之前我们讨论的几个例子,都是理赔次数服从泊松分布,现在还需讨论复合二项、负二项分布,其他条件同上例。当理赔额分布为帕累托分布时,再保险人获得保费:
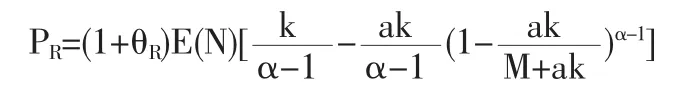
扣除再保险费后,原保险人剩余保费为:
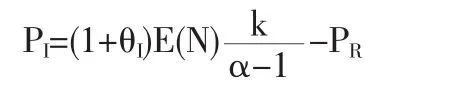
准则(2)下的最优再保险策略为:
与一次理赔额服从指数分布时一样,联合生存概率随理赔次数方差增大而变小。与指数分布比较,帕累托分布的联合生存概率整体偏小,这是因为帕累托分布的尾部较指数分布更重,尾部风险更高。
4 结论
在聚合风险模型下,原保险人和再保险人的理赔总额分布为复合分布,一般无法得到精确解,而双方理赔总额的联合分布更难获得,因此,只能尝试用近似方法处理此类问题。我们首先讨论了原保险人和再保险人理赔总额的边际分布,给定再保险策略以及理赔次数和理赔金额分布,进行平移伽马分布近似。而后,运用椭球型连接函数(copula),刻画原保险人和再保险人理赔总额的相关性和尾部相依性,从而得到了近似双方理赔总额联合分布的最优方法。本文提供的方法可用于研究保险精算中与联合分布函数相关的内容,例如:条件概率,给定初始准备金后的联合生存概率,保证收益率前提下的联合生存概率等等。因此便有了更多的新的优化准则可供选择,为研究再保险优化问题拓宽了思路。
[1]Klugman S.A.,Panjer H.H.,Willmot G.E.Loss Models:From Data To Decisions[M].Chichester:Wiley,2004.
[2]Hardy M.R.Approximating the Aggregate Claims Distribution,Encyclopaedia of Actuarial Science[M].Chichester,Wiley,2004.
[3]Glasserman P.,Heidelberger P.,Shahabuddin P.Portfolio Value at Risk with Heavy Tailed Risk Factors[J].Mathematical Finance,2002,12.
[4]Demarta S.,McNeil A.J.The Copula and Related Copulas[J].International Statistical Review,2005,73.
[5]Embrechts P.,McNeil A.,Straumann D.Correlation and Dependence in Risk Management:Properties and Pitfalls[M].Cambridge:Cambridge University Press,2001.
[6]Cai J.,Tan K.S. Optimal Retention for a Stop-loss Reinsurance under the VaR and CTE Risk Measure[J].Astin Bulletin,2007,37(1).
[7]Gajek,L.,Zagrodny,D.Optimal Reinsurance under General Risk Measures[J].Insurance:Mathematics and Economics,2004,34.
