随机利率下的连续型增额寿险精算研究

2010-05-22信恒占

统计与决策 2010年7期

信恒占

（河南大学金融证券研究所，河南开封 475004）

0 引言

在传统的精算理论中，假定利率是确定的，实务中的利率是具有随机性的，从而会引起利率风险。利率随机性的研究在近20年来逐步受到重视。人们开始注意到，由利率随机性产生的风险对寿险公司而言可能是相当大的。根据传统的精算原理，由死亡率随机性产生的风险，利用大数定律可以通过出售大量的保单来分散，但是由利率随机性产生的风险，不可能通过增加销售量来分散，因为即使是很大的保险公司，其每张保单一般采用同一利率，或采用十分接近的利率。因此，利率风险要比死亡率风险对保险公司的影响更大，若保险公司假定未来利率是一固定常数进行保费测算，很可能会对寿险公司造成巨大损失。所以如何合理、准确地预测利率具有重要意义。寿险中的利率随机性问题成为近年来保险精算研究的热点之一。

1 预备知识

1.1 生存模型中的常用符号

（1）(x)表示岁的人；

（2）T(x)表示年龄为岁的人的剩余寿命；

（3）K(x)表示岁的人的整值剩余寿命；

（4）tpx表示岁的人至少活到x+t岁的概率；

（5）tqx表示x岁的人在t年内死亡的概率；

（6）μx表示x岁时的死亡力，即活到x岁的人在后一瞬间死亡的概率。

T(x)的概率密度函数为 fx(t)=tPxμx+t。

1.2 确定利率下的增额寿险

假设利息力 δ≥0为常数，则折现函数 vt=e-δt，t时刻的给付现值

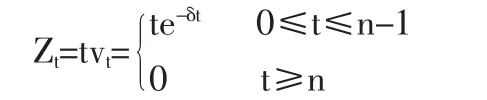
给付现值是随机变量，我们将这个随机变量记为ZT。则

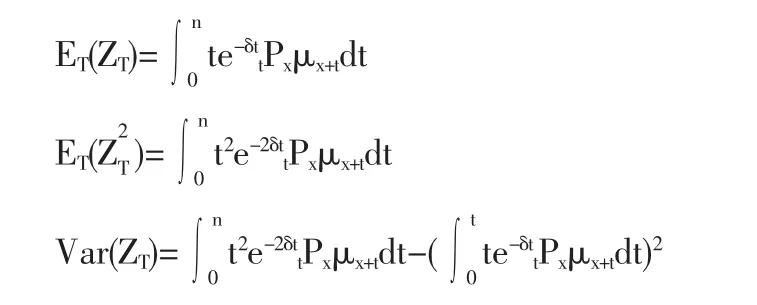
2 模型假设

（1）保险期限为n年，被保险人如在第n年末尚未生存，则保险人不给付保险金；被保险人如在年n内不幸死亡，则保险人当即给付相应的保险金，保额为t。

（2）利率的运动过程由两部分组成：一是“正常”的波动，由一些细小信息的到达使得利率产生一些波动，考虑利率的恒正性，在此用在原点反射的布朗运动来刻画。

若一个连续型的过程满足以下三个条件，我们称之为Brown运动。

①W(0)=0；

②增量是独立平稳的；

③W(t)服从均值为0，方差σ2t为的正态分布。

（3）利率的运动过程其二是“非正常”的波动，由于一些重大信息的到达使得利率产生较大的波动，用Possion过程来刻画。

Poisson过程是计数过程的最重要的类型之一。所谓计数过程，是指一随机过程{N(t),t≥0},其中N(t)表示到时刻为止已发生的“事件”的总数。

若计数过程{N(t),t≥0}其中含有参数λ＞0，满足如下条件：

①N(0)=0；

②过程具有独立增量；

③在任一长度为T的区间中事件的个数服从均值λt为的 Poisson 分布。即对一切 s,t≥0，有 P{N(t+s)-N(s)=n}=e-λtm=0,1,…），则称计数过程为Poisson过程。

从条件（3）可知，Poisson过程有平稳增量，且E(N(t))=λt，因此称λ为此过程的速率或强度，即单位时间内发生事件的平均个数。

（4）常见的死亡力假设

在建立精算模型时，知道被保险人的死亡分布是十分重要的，而在连续型寿险精算模型下，死亡力更是影响被保险人剩余生命函数T(x)的分布函数、密度函数的重要因素。下面，我们将介绍一下四种常见的死亡力解析形式。对死亡力有不同的假设，常见的有De Moivre死亡律、Gompertz死亡律、Makeham死亡律、DeWeibull死亡力等。本文将在以上四种死亡力假设下给出增额寿险的精算现值和方差的公式。

①De Moivre形式

该式于1729年由De Moivre建立，在该形式下，随机变量X的概率分布及密度函数的形式如下：

从以上的生存函数、密度函数可以看出，若死亡力满足De Moivre形式，随机变量X在[0，w]上是服从均匀分布的。

②Gompertz形式

其死力函数为：μx=BCx(x≥0)，其中，B＞0，C＞0。

该式于1825年由Gompertz建立，在该形式下，随机变量X的概率分布及密度函数的形式如下：

③Makeham形式

其死力函数为：μx=A+BCx(x≥0) ，其中，B＞0，C≥1，A≥-B。

该式于1860年由Makeham建立，在该形式下，随机变量X的概率分布及密度函数的形式如下：

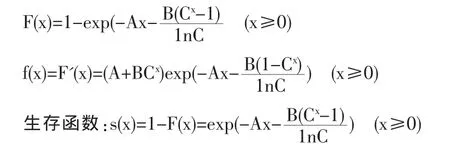
特别地，当A=0时，Makeham形式可以简化为Gompertz形式，可以说Gompertz形式是Makeham形式的推广。

④Weibull形式

其死力函数为：μx=kxn(x≥0)，其中 k＞0，n＞0。

该式于1939年由Weibull建立，在该形式下，随机变量X的概率分布及密度函数的形式如下：

F(x)=1-exp(-k(n+1)xn+1)

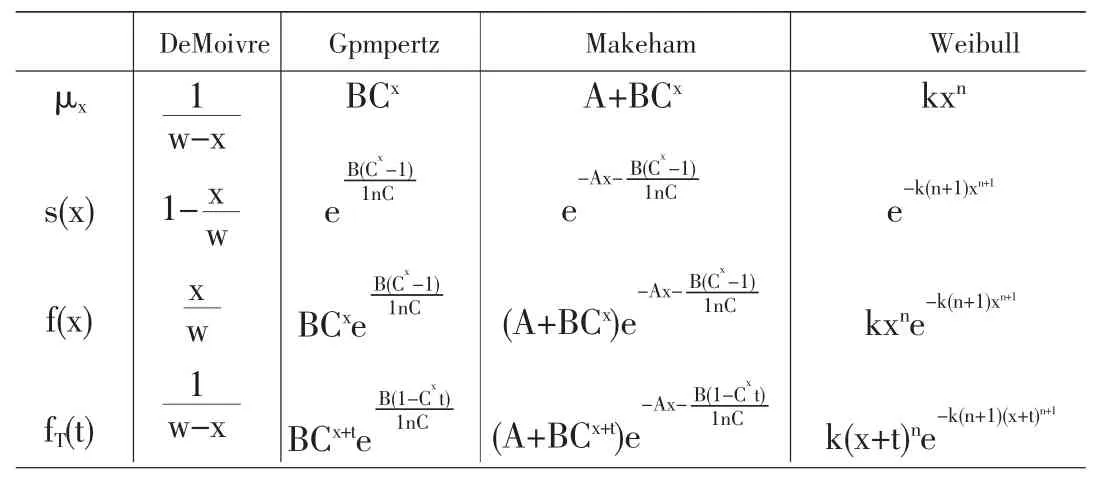
表1 四类死亡力解析形式下生存函数的对照表

f(x)=F'(x)=kxnexp(-k(n+1)xn+1) (x≥0)

生存函数：s(x)=1-F(x)=exp(-k(n+1)xn+1) (x≥0)

综上所述，在四种死亡力的解析形式下，密度函数和生存函数，以及被保险人(x)的剩余生命随机变量T的分布和莫度函数归纳如表1。

3 模型的建立

在此由反射Brown运动与Poisson过程联合对利率建模，利息力累积函数：

R（t）=δt+β|W(t)|+γN(t)

其中，|W(t)|为在原点反射的布朗运动，W(t)为一标准的布朗运动，W(0)=0，N(t)为一 Possion 过程；W(t)与 N(t)相互独立；δ,γ,β 均为常数。

t时刻的给付现值为：

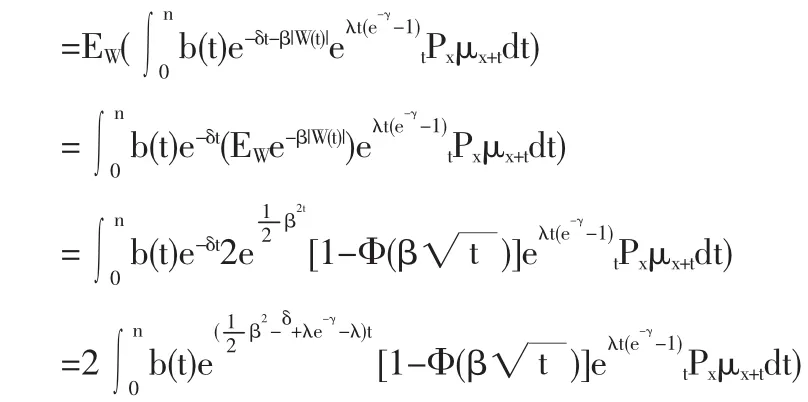
（2）二阶矩及方差的公式

4 联合建模下精算现值和方差的计算

4.1 De Moivre假设下各种增额寿险的精算现值和方差

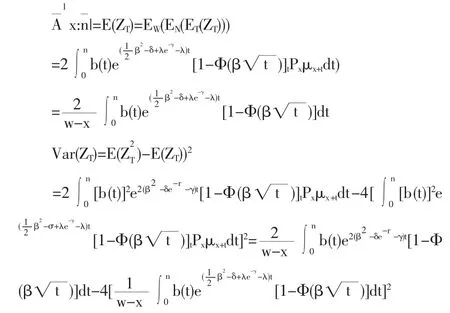
(1)当保额为逐年增加的增额寿险即b(t)=a+bt时的精算现值和方差的表达式

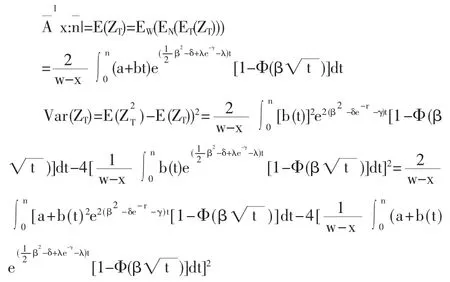
(2)当保额为按几何增长的增额寿险即b(t)=tk(k=2,3,…)的精算现值和方差的表达式

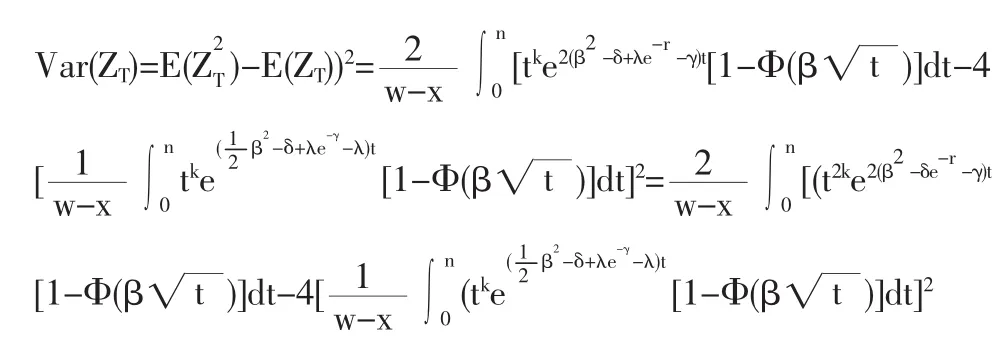
(3)当保额为按指数增长的增额寿险即b(t)=ert(r＞0)时的精算现值和方差的表达式

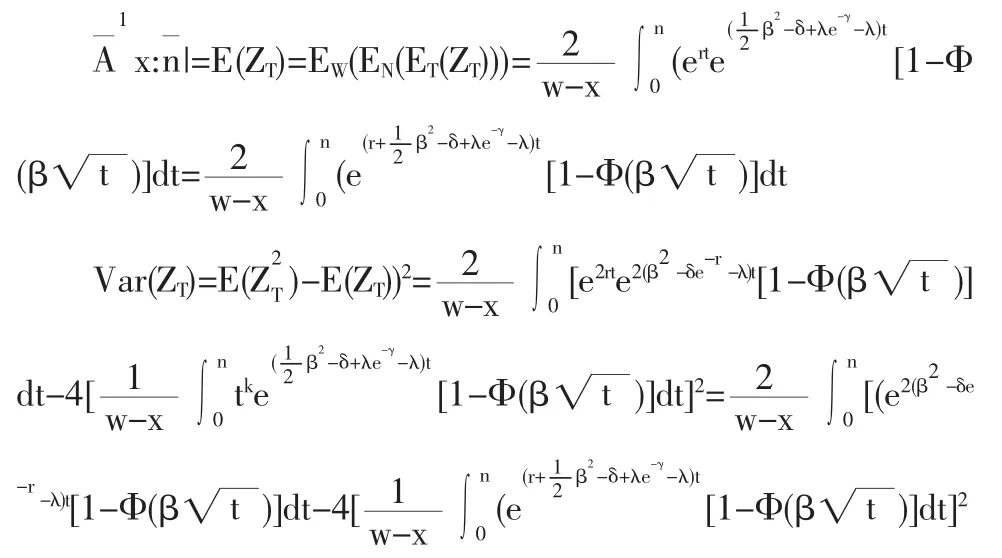
4.2 Gompertz假设下各种增额寿险的精算现值和方差

(1)当保额为逐年增加的增额寿险即b(t)=a+bt时的精算现值和方差的表达式

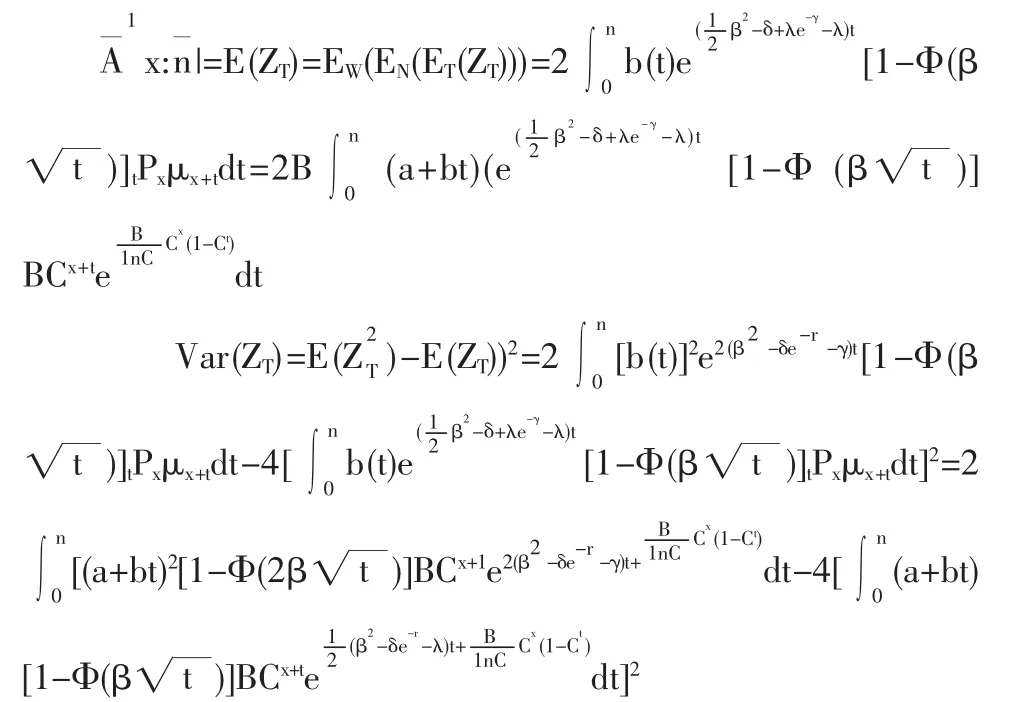
(2)当保额为按几何增长的增额寿险即b(t)=tk(k=2,3,…)的精算现值和方差的表达式

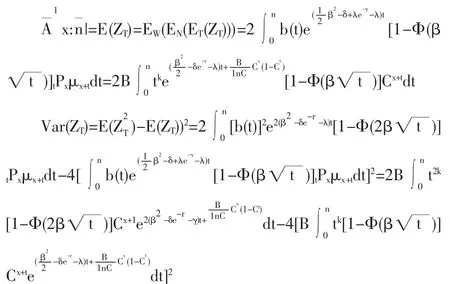
(3)当保额为按指数增长的增额寿险即b(t)=ert(r＞0)时的精算现值和方差的表达式

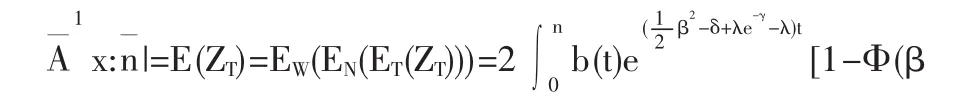
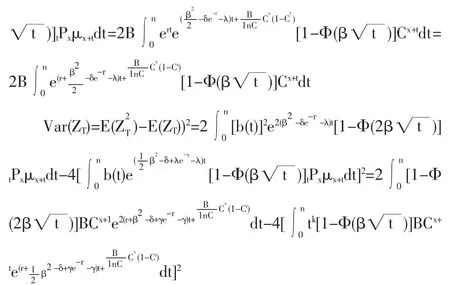
4.3 Makeham假设下各种增额寿险的精算现值和方差

(1)当保额为逐年增加的增额寿险即b(t)=a+bt时的精算现值和方差的表达式

(2)当保额为按几何增长的增额寿险即b(t)=tk(k=2，3，…)的精算现值和方差的表达式

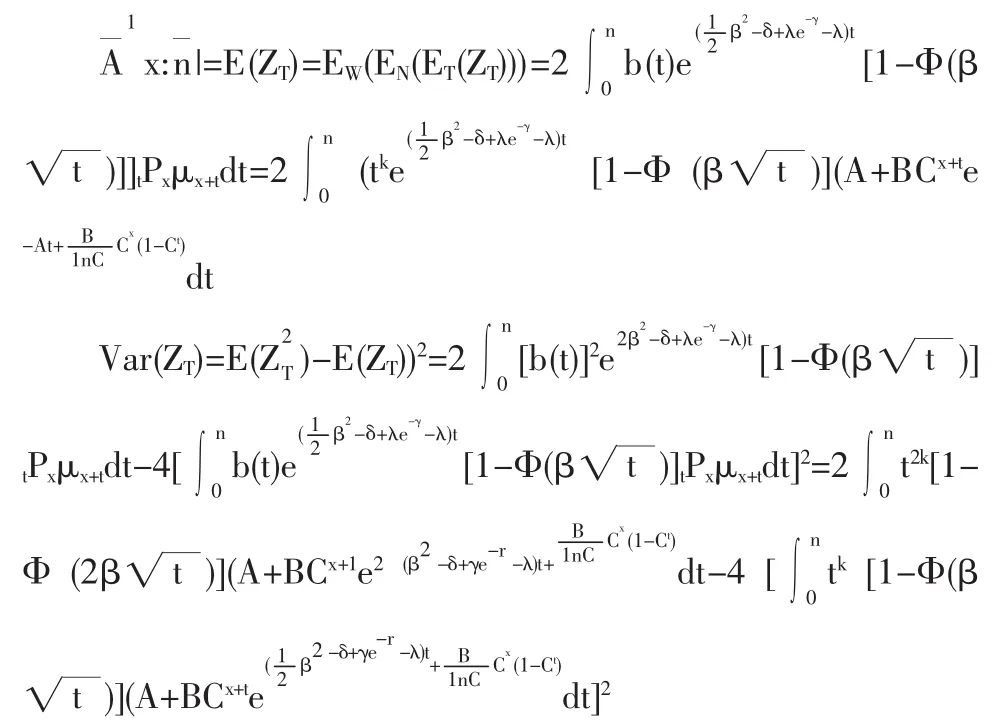
(3)当保额为按指数增长的增额寿险即b(t)=ert(r＞0)时的精算现值和方差的表达式

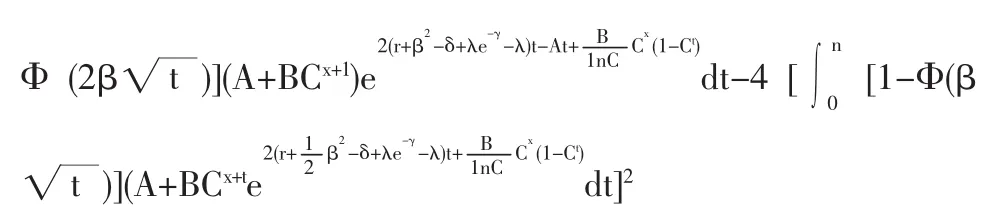
4.4 Weibull假设下各种增额寿险的精算现值和方差

(1)当保额为逐年增加的增额寿险即b(t)=a+bt时的精算现值和方差的表达式

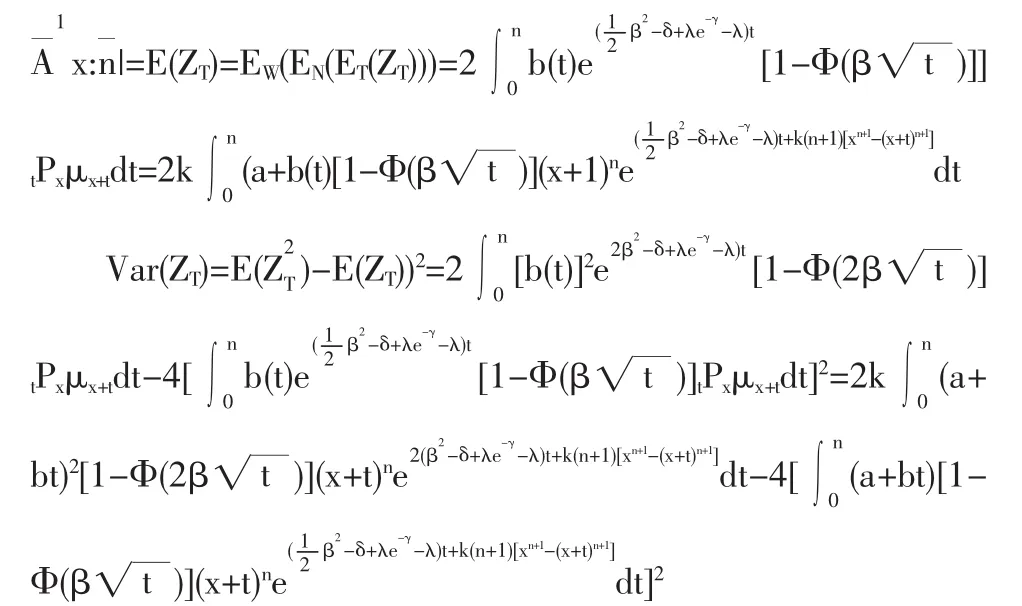
(2)当保额为按几何增长的增额寿险即b(t)=tm(m=1，2，…)的精算现值和方差的表达式

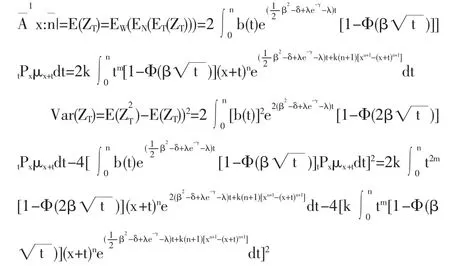
(3)当保额为按指数增长的增额寿险即b(t)=ert(r＞0)时的精算现值和方差的表达式

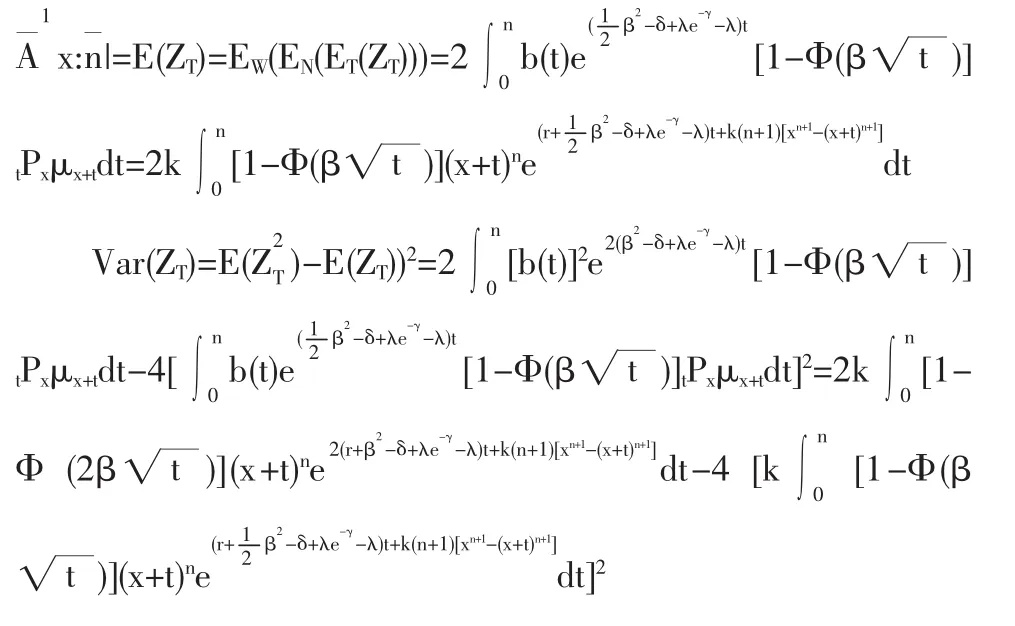
5 结束语

本文对传统精算学中固定利率进行了改进,考虑到随机利率的影响,根据双随机性,利用反射布朗运动和泊松分布联合建立息力积累模型。利率的运动过程由两部分组成：一是“正常”的波动，由一些细小信息的到达使得利率产生一些波动，考虑利率的恒正性，在此用在原点反射的布朗运动来刻画；其二是“非正常”的波动，由于一些重大信息的到达使得利率产生较大的波动，由Possion过程来刻画。针对连续型增额寿险，给出各阶矩的表达式，很容易算出精算现值及方差值，从而可以确定所述各种增额类型的趸缴保费，具有一定的实际意义。更加符合保险实务的要求,具有更广泛的使用范围,相应的结论也更具有一般性,这对寿险公司风险管理有重要的理论指导意义；随机利率的引进，可以避免或减小利率风险对保险公司的影响。当β=0,γ=0时，模型变成了常数利率下的情况；当n→∞时,n年期增额寿险变成终身寿险。

[1]Abraham Z.Annuities under Random Rats of Interest[J].Insurance:Mathematics And Economics,2001，(28).

[2]王传玉.一类随机利率下的增额寿险[J].运筹与管理，2005，(4).

[3]魏静,王永茂.随机利率下全连续式增额寿险模型的责任准备金[J].燕山大学学报，2006，(3).

[4]陈海兵，韩素芳.一类随机利率下的变额寿险模型研究[J].数学理论与应用，2008，(9).

[5]高建伟，邱苑华.随机利率下的生存年金模型[J].系统工程理论与实践，2002.

[6]郭春增,王秀瑜.随机利率下的寿险精算模型[J].统计与决策，2008，(9).

[7]何文炯，蒋庆荣.随机利率下的增额寿险[J].高校应用数学学报，1998，13A(2).

[8]郎艳怀，冯恩民.随机利率下的综合人寿保险[J].大连理工大学学报，2001，41(5).

[9]李秀芳，傅安平，王静龙.保险精算[M].北京：中国人民大学出版社，2008.

[10]田吉山，刘裔宏.随机利率条件下的寿险模型[J].经济数学，2000，（3）.

[11]刘凌云，汪荣明.一类随机利率下的增额寿险模型[J].应用概率统计，2001，(3).

[12]欧阳资生.随机利率下增额寿险现值函数矩的一些结果[J].经济数学，2003，（3）.