基于保险行业新投保、续保、理赔综合性SPSS数据分析报告
2021-07-03杨鸿志四川大学锦城学院计算机与软件学院
杨鸿志 杨 杉(四川大学锦城学院计算机与软件学院)
■ 前言
保险,是指投保人根据合同约定,向保险人支付保险费,保险人对于合同约定可能发生的事故因其发生所造成的财产损失承担赔偿保险金责任,或者被保险人死亡、伤残、疾病或者达到合同约定的年龄、期限等条件时承担给付保险金责任的商业保险行为。
从经济角度看,保险是分摊意外事故损失的一种财务安排;从法律角度看,保险是一种合同行为,是一方同意补偿另一方损失的一种合同安排;从社会角度看,保险是社会经济保障制度的重要组成部分,是社会生产和社会生活“精巧的稳定器”;从风险管理角度看,保险是风险管理的一种方法。
为了尽可能规避保险风险,获得更大的利益,并且在此过程中体会理财的难度,为更多人的保险选择以及保费范围提出中肯的建议,我寻找到三份涉及新投保、续保、理赔的数据报告,并提出相应问题进行探究。笔者带着“过去三年平均年收入与总保费之间是否相关”等3 个问题,通过对新投保(续保信息内容与新投保内容较为一致)90 万条数据(包含投保机构,险种,投保时间,缴费方式,缴费期限,投保份数,总保费,保额,投保客户的客户号,性别,年龄,婚姻状况,过去三年平均年收入,教育程度,职业,家庭人口)的excel 数据表,提炼出关于投保机构,险种,总保费,保额,客户个人信息(性别,年龄,婚姻状况,职业,过去三年平均收入)这几个重点,对理赔21 万条数据(包含投保机构,险种,案件号,保单号,赔款金额,赔款时间,费用类型,总保费,保额,投保客户个人信息),进行SPSS 制图和数据分析,探究以平均年收入与总保费之间简单相关性为主的数据之间的关系,进行数据分析并提出结论和建议,做此分析报告。
■ 研究思路
将三个excel 表进行基础整理,去掉对本分析无用的行列,从而减少数据数目,然后使用SPSS 打开,使用SPSS 的线性回归分析、相关性分析、区间估计、分析描述统计中的探索功能等分析方法逐步分析,在探究投保数据时总保费与保额年龄、过去三年平均收入的线性回归数据分析,在续保的表格里探究不同性别的区间关系,在保额的数据表里面探究相关数据,如不同性别与总保费、保额之间的关系,在理赔的保险里对总保额、保费和赔款金额进行SPSS 分析,分析其两两变量之间的影响,得出相对应的计算公式,理清数据之间的影响因素,得出最终结论。
■ 数据说明
(一)数据来源
数据来源于某保险公司新投保数据表(90 万条),续保数据表(21 万条),理赔数据表(21 万条)。
(二)数据清洗
我们对excel 数据工作表做了两方面的清洗工作:第一是对与研究问题无关的行列进行删除和简单的整理排序,将无用的列或者是信息不完整的列或行进行删除,另外对部分不合理的数据进行筛查,看其数值是否异常。第二是注释性别F 指女性,M 指男性,婚姻状况S 指未婚,M 指已婚,D 指离异,X 指未知。并且将客户号一列的科学计数法变为常规计数法。再用SPSS 软件将其打开,并对数据进行区间估计以及双变量数据分析。
■ 投保数据分析
(一)新投保数据分析
总保费与保额、年龄、过去三年平均年收入的线性回归数据分析。
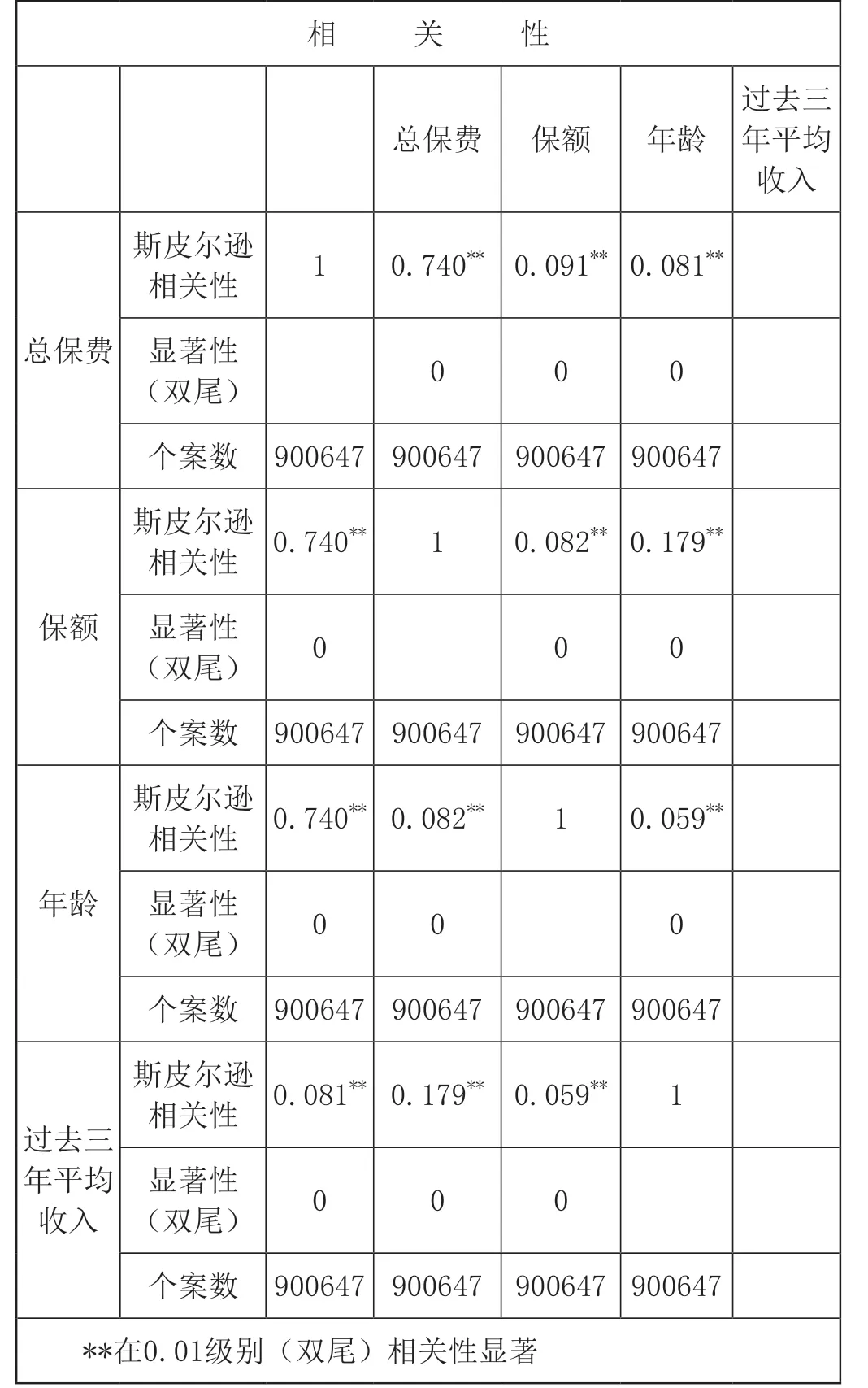
图1 总保费与保额、年龄、过去三年平均年收入的线性回归数据分析
如图1 所示,先对总保费、保额、年龄与过去三年平均收入分别做一个简单相关性分析,因显著性大于0.01 则为相关,由此我们可以分析得出结论,即根据斯皮尔逊相关性来分析,保额与年龄还有过去三年的平均收入都呈显著相关,这也就说明在我们投保新的总保额时,我们往往会考虑自身的收入和年龄以及保额的影响,从而根据我们自身的情况来进行总保额的选择。同时从保额的斯皮尔逊分析结果来看,保额和总保费与过去三年平均收入均有显著性相关,由此结果我们可以知道,人们随着年龄的增加可能个人的收入也在增加,从而加大了对保额的投保。从年龄的斯皮尔逊结果来看我们不难发现,年龄和总保费有着显著相关结果。由此可见,当我们随着年龄的增大时,我们想要买入的保险份额可能也随之增加。当我们看到过去三年平均收入的斯皮尔逊相关系数时,我们不难发现,过去三年平均收入和总保费与保额均呈现显著性相关,由此结果我们可以看出,当人们的收入提高时,人们自然而然就会对所购买保险的费用进行加大,从而保费的额度与之相应增大。
(二)续保数据分析

图2 不同性别之间续保额区间估计的数据分析
先点击分析——描述统计——探索,再根据我们的问题,将保额作为因变量,性别作为因子,接着点击右上角的统计将置信区间改为95%,最后点击继续,下方的输出样式选择统计表。
对不同性别之间的保额做区间分析之后,由图2 知道保额与续保额呈现逐相关性的。由图2 可知:男女性的数据都为真实有效的,并且缺失值为0。又可知,男性女性的峰度都大于0,说明不同性别与保额之间都成正态分布,而男性女性的偏度都大于0,则说明其分布较正态、分布曲线更向右偏,称为正偏或右偏,说明存在偏大的极端值,并且男性的极大值大于女性的极大值。而在对于平均值95%置信区间的对比中我们看出,女性的续保额区间要比男性的高。由图一可知这大概率是因为一方面由于年龄的增加我们的过去三年平均收入也随之增加,所以我们的续保额也随之增加,由图二又可知,女性在选择续保保险的类别范围是比男性小的,在一定程度上导致了男性的选择种类多,因为续保的金额不同,但并不是每个都会大笔投入。而女性选择更加单一化,投入的资金更倾向于之前所买的,所以也随之而增加了其续保额的投入,所以在对于平均值95%置信区间的对比中我们看出,女性的续保额区间要比男性的高。
(三)理赔数据分析
不同性别理赔总保费的区间估计。

图3 不同性别总保费的区间估计
步骤:先点击分析——描述统计——探索,再根据我们的问题,将总保费作为因变量,性别作为因子,接着点击右上角的统计将置信区间改为95%,最后点击继续,下方的输出样式选择统计表。
如图3 所示,对不同性别保费做区间估计后,得出结论:根据男性与女性的平均值数据,男性的总保费是要高于女性的,因为男性在中高档之间的保额是远大于女性的,又因为保费和理赔额之间呈显著相关,且男性女性的峰度都大于0,说明不同性别与理赔总保费之间成正态分布,这也就可知,男性的保险种类买的比较多,所以理赔总额也会比较高。而男性女性的偏度都大于0,则说明其分布较正态、分布曲线更向右偏,称为正偏或右偏,说明存在偏大的极端值。而在对平均值95%置信区间的对比中我们看出,女性的总保费区间要比男性的低。
而根据箱型图我们可以得知,男性和女性总保费的分布也不一样,男性极端值大于女性的,但是女性有两个极端值情况,在二十万到六十万的区间,男性的人数明显多于女性,也因此说明了男性的大金额的人数要比女性的多一点。而在二十万这个区间上下,女性的人数是明显多于男性的。在二十万以下的情况里可以看到女性的人数是明显比男性更加偏向底部,而男性的分布则更加均匀。
■ 总结
从三张不同的表格分析数据来看,保险的保额、保费、退保额与三年的平均收入成正比关系。不仅如此,对于推销人员来说,从保险数据的表格来看,男性和女性总保费的大致分布有一定区别,男性更偏向于中高档的保险种类,但是其续保额可能不如女性的多一点,女性的保额区间较高于男性,但是男性的赔大金额的人数要比女性的多一点。我们可以选择将大额理赔推销给男性顾客,在续保时,我们可以尝试将不同的保险类型推销给男性群体,将保额区间高一点的推销给女性客户,并且在续保时推销同种或同类型的保险种类给女性群体。对消费者来说,从三张保险的数据分析来看,在一定的年龄范围内,我们对于保险的额度会往较高的方向去选择,而赔款金额也会相应较高,自然而然的我们投保的金额也会增加。所以,我们不妨在选择保险时可以考虑保额时间较长的险种,这样对我们后续的投入和保额的要求以及保额的赔款金额要求都会得到相应满足。
