双寡头垄断市场下研发投入竞争的决策选择
2010-05-22陈积志任方旭
陈积志 ,任方旭 ,2
(1.河海大学 商学院,南京 210098;2.中原工学院 经济管理学院,郑州 450007)
在企业研发合作与竞争方面的文献中,多以合作研发为研究对象,并以降低成本作为研发的主要目的,在模型建立上,基本都来自于 Katz(1986)[1]和 D’Aspremont&Jacquemin(1988)[2]尤其是后者提出的博弈模型,几乎每一篇合作创新或合作研发的文献都会提到这一模型(A-J模型),并在其基础上进行拓展和延伸。而对于研发竞争研究的文献相对较少,Ziss&Stefen(1994)构建了一个有溢出的两阶段R&D双寡头博弈模型,将不合作方式与合作研发(研发勾结)、价格安排(在生产阶段勾结)及合并(研发和生产阶段均勾结)等三种勾结方式一一作了比较,并评价了各种勾结方式改善福利的条件[3]。Damiano研究了研发投入市场中的合作和竞争,并对其进行了比较[4]。国内这方面的文献也较少,楼高翔等研究了双头市场中的具有一定生命周期的产品开发竞争[5]。张光宇等研究了双寡头垄断市场中新技术研发投资的动态博弈问题,其假设市场为刚性需求且需求量相对不变,新技术研发的结果表现为降低企业生产成本[6]。惠静薇等对双寡头竞争企业的R&D方式给予了分析,并给出了最优投资收益[7]。
事实上,对于当前买方市场所形成的企业竞争的加剧以及“渠道为王”中所出现的零售商逐渐成为供应链主导者这样的实际情况,企业的研发创新的竞争焦点已经从“消化吸收阶段”的“降低成本”转化为“改进创新阶段”的“改进产品性能”,以满足新市场的需求。因此,技术研发的结果主要表现为提升最终产品品质,进而提升最终产品在市场上的议价能力。本文将以提升产品品质以增加市场需求为研发投入的主要目的,利用简单的线性函数模型对双寡头垄断市场下企业研发投入竞争进行分析,给出两寡头企业利润最大化下的最优研发投入的均衡解,并考虑相关的信息不对称情况。
1 完全信息下的静态研发投入竞争
设寡头垄断市场上有两个在位厂商1和2展开研发竞争,每个企业根据对手采取的行动,并假定对手继续如此行事,来做出自己的研发投入决策。各厂商根据对方的研发策略,不断调整自己的选择策略。两个寡头企业生产同样的产品,表现为不变的规模经济,单位生产成本分别为ci(i=1,2)。两厂商选择的研发投入分别为xi(i=1,2),产品单位研发投入所产生的市场平均需求为βi(i=1,2),它反映了企业以追求产品品质为目的的研发投入的市场效益,一般可从一年中产品的销量与研发投入总量的比值并加以处理来求得。这样,市场投入x(x=x1+x2)研发数量后所产生的产品需求为q=q1+q2=βx=β1x1+β2x2。另外,假设两寡头厂商面对相同的线性需求函数为:
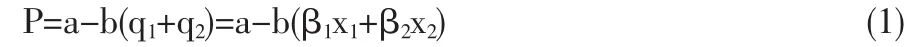
这种假设与文献[8]的思想一致。对于研发产品的企业,其不变成本主要就是企业的研发费用,而企业的可变成本,我们已设置为ci(i=1,2)。
两个寡头企业追求:

联立两企业的反应函数(3)式,可得到企业利润最大化下的最优研发投入水平为:
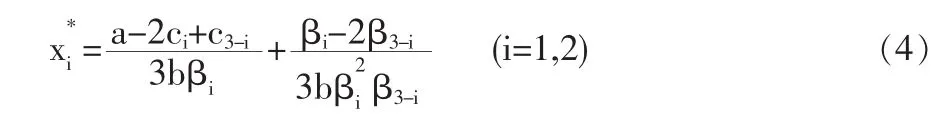
此时,两厂商的最大化利润为:
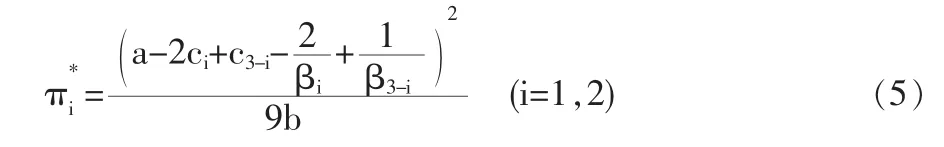
这表明研发投入竞争时企业所获得的利润大小不仅与双方产品的单位生产成本有关,还与双方企业单位研发所产生的市场平均需求有关。企业单位生产成本越小、研发所产生的市场平均需求越大,则企业所获得的利润就越大。
现实中,企业不仅追求自己的利润水平高于竞争对手,而且追求自己的研发投入低于对手,以使得以较小的投入产生较大的产出效果。即企业1要追求。为了简便,我们分两种特殊情况来加以分析。
(1)当两企业单位生产成本相同时
将两个寡头企业视为同等生产条件,此时,它们的单位生产成本 ci相等,即 c1=c2=c0。由利润大小条件易得 β1>β2。由两企业的最优研发投入可得满足x1<x2的条件为
因此,在两企业具有相同单位成本下,企业1要追求以较小的研发投入产生较大的利润水平,则其研发投入所产生的市场平均需求需同时满足β
(2)当两企业产品单位研发投入所产生的市场平均需求相同时
此时,β1=β2=β0,由利润大小条件易得 c1<c2。 由两企业的最优研发投入(4)式可得满足 x1<x2的条件为 c1>c2,显然矛盾。故在研发投入所产生的市场平均需求相同条件下,企业不可能实现以较小的研发投入产生较大利润水平的情况。
作为同等生产条件下的特例,我们假定两个企业的单位研发所产生的平均需求相等,即β1=β2,这时,两企业 x1=x2、π1=π2,这说明两个完全对等的寡头企业在研发投入所产生的市场平均需求相同条件下,其研发投入水平相同,且获得的利润水平也相同,这与企业的古诺产量竞争相类似。
因此,寡头企业利润最大化下的研发投入不仅取决于自己研发竞争下的单位生产成本和研发投入所产生的市场平均需求,而且也取决于对方的情况。
2 完全信息下的动态研发投入竞争
此时,每个企业根据对方的研发策略,不断调整自己的选择策略。两个参与企业中,假设寡头企业1为领导者(或在位者),企业2为跟随者(或新进者)。企业1可以利用企业2的反应函数作为研发投入决策的依据,企业2在企业1研发投入基础上,制定企业1的研发投入以实现利润最大化;企业1再依据企业2的研发投入来制定自己的收益水平。
企业1预计到企业2对研发水平x1所做的反应。针对x1,企业 2 追求:

由(4)式可知企业2的反应函数为:

企业1把企业2的反应函数 (7)式代入自己的利润函数,并最大化得到其最优研发水平为:

将(8)式代入(7)式,可得企业2的实际均衡研发投入水平为:

此时,两企业的利润分别为:
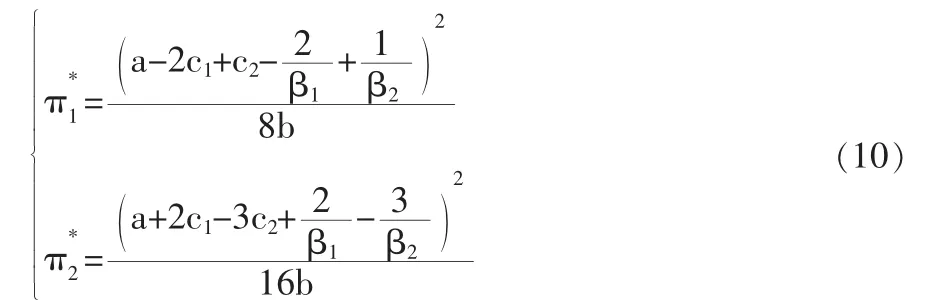
(1)领头企业的“先动优势”
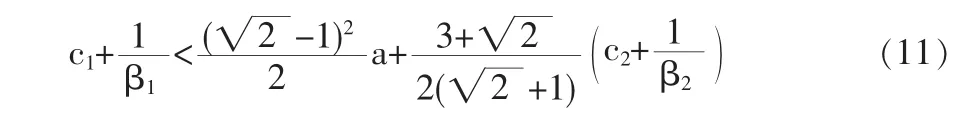
另外,由于两企业的研发投入不小于零,故由(8)、(9)两式可得:
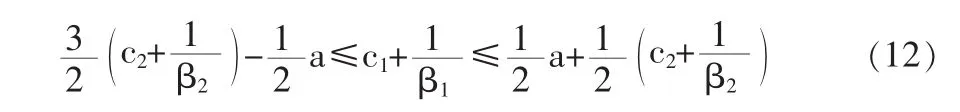
因此,领头企业1要获得抢先优势,优先获取研发产生的产品需求,并通过限制企业2的研发规模来获得比企业2更多的利润,其成本及研发投入效益需满足:
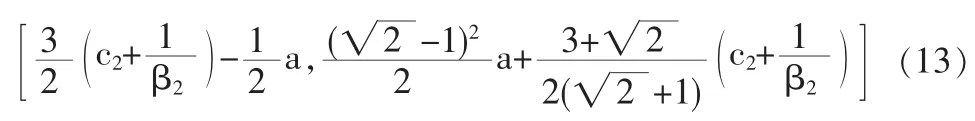
企业1作为领头企业,不仅追求最大化的利润高于对手,有时还追求由研发所产生的市场占有率要高于对手。这里假定企业的市场占有率为k,要使企业1产品具有更高的市场占有率,需满足:

因此,领头企业在观察到跟随企业的研发投入后,要使自己具有研发抢先的竞争优势,既要满足最大化的利润高于对手,又要比对手的市场占有率更高,则领头企业的成本及研发投入效益必须同时满足(13)、(15)两式。
(2)跟随企业的“后发优势”
对于跟随企业,在领先企业成本及研发投入效益既定条件下,进入研发市场的条件必须要使自己的未来利润大于零,由(10)式可得:

这表明,在企业1研发抢先情况下,若企业2不具备综合优势,获利就很少。这种研发的抢先投入是市场进入壁垒的一种形式。
企业2作为跟随企业,要通过研发效应产生出比对手更高的市场占有率,即要使企业2产品具有更高的市场占有率,这就需要满足:

要使跟随企业具有“后发优势”,企业2不仅要使产品具有更高的市场占有率,而且自身所获得的均衡利润要高于领头企业,即还要使根据(10)式可得:
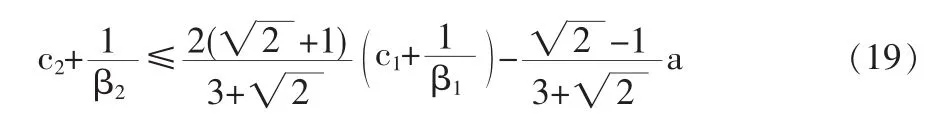
当同时满足(18)式和(19)式时,跟随企业的综合优势较强,就会削弱领先企业的抢先优势。领先企业的抢先研发投入就会成为部分浪费;跟随企业将可以以非常低的成本冲破领先企业的研发防线,以具有更好的竞争优势。
3 不完全信息下的动态研发投入竞争
在前面的分析中,我们假定了企业的单位生产成本以及单位研发投入所产生的市场平均需求是博弈双方的共同知识。事实上,这两个变量的信息是不对称的。为了讨论与企业研发有关的情况,这里假定两企业具有对等的生产条件(c1=c2=c0),在位企业1不能够确定企业2(假设为研发市场的新进企业)的单位研发投入效益高低,它只知道进入企业2的研发投入所产生的市场平均需求为高(β2H)的概率是1-u,低(β2L)的概率是 u。
这样,企业 1 追求 max[a-b(β1x1+β2x2)-,而企业2的目标函数具有两种特征类型:研发投入所产生的市场平均需求高、低情况,由企业2的利润最大化条件可解得其研发投入的两种情况为:

企业1在进行决策时,由于不知道企业2的具体研发投入效益情况,所以无法准确确定对方的研发投入的类型,只能根据其对于企业2到底属于何种研发投入效益类型概率来加以估计,并对本企业的利润进行期望意义上的最大化决策,即企业1的期望收益E(Π1)为:

从而企业1的研发投入水平为:
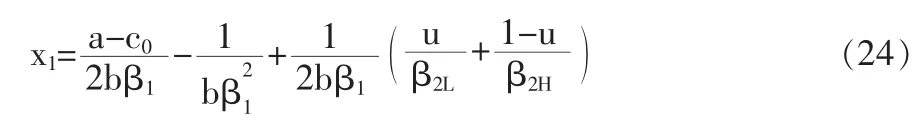
代入x2的表达式,可以得到企业2两种情况下的研发投入水平为:

由于信息的不对称,在位企业1不知道新进企业2的单位研发投入效益情况,但企业2明确了解自己的概率情况。当企业1预测企业2的研发投入所产生的市场平均需求概率为低时,其研发投资将减少),而相应的企业2的研发投入将增加)。当企业1预测企业2的研发投入所产生的市场平均需求概率为高时,其研发投资将增加),而相应的企业2的研发投入将减少)。
因此,由于信息不对称,两企业研发投入数量的改变取决于在位企业对新进企业研发投入效益类型的预测。
4 结束语
在寡头垄断市场条件下,本文对双寡头企业研发竞争的博弈模型进行了较具体地分析。在完全信息静态研发投入竞争下,分析了企业以较小的研发投入产生较大利润水平的情况。在完全信息动态研发投入竞争下,给出了领头企业的“先动优势”以及跟随企业 “后发优势”的条件。领头企业在完全信息下的动态竞争与静态竞争相比,其研发投入将会增加,且获得的利润水平也随之增加,并高于对方。而在研发投入效益类型信息不对称下,企业的最优研发投入数量将会改变,其改变的多少取决于在位企业对新进企业研发投入效益类型的预测。
由于篇幅所限,本文没有分析信息不对称时的静态竞争及动态竞争的企业收益情况。另外在分析信息不对称时,本文假设企业的单位生产成本对等。事实上,竞争企业的成本信息也是不对称的。对于各变量都处于不完全信息市场条件下以及多寡头企业研发投入竞争,特别是多阶段动态竞争的情况我们将另文讨论。
[1]Katz M.L.An Analysis of Cooperative Research and Development[J].Rand Journal of Economics,1986,(17).
[2]D’Aspremont C,Jacquemin A.Cooperative and Non-Cooperative R&D in Duopoly with Spillovers[J].American Economic Review,1988,78.
[3]Ziss,Stefen.Strategic R&D with Spillovers,Collusion and Welfare[J].Journal of Industrial Economics,1994,(XLII(4)).
[4]Damiano Bruno Silipo,Avi Welss.Cooperation and Competition in an R&D Market with Spillovers[J].Research in Economics,2005,59(1).
[5]楼高翔,曾赛星.基于产品生命周期的双寡头市场产品开发竞争[J].科学学研究,2005,23(B12).
[6]张光宇,肖伟.双寡头垄断市场中新技术研发投资的动态博弈[J].系统工程,2006,24(7).
[7]惠静薇,马百铭.双寡头竞争企业的R&D方式与最优投资收益分析[J].科技管理研究,2007,27(7).
[8]钟胜.寡头供应链企业间合作竞争策略研究[D].成都:西南交通大学管理学院,2007.
