不等间隔动态数据的灰色建模

程毛林

(苏州科技学院 数理学院，江苏 苏州 215009）

0 引言

在很多实际问题中，有时采集的历史数据不多，因而多数统计预测方法的效果往往不理想，而灰色预测方法特别适合于贫信息场合，在原始时间序列点数较少的情况下仍能作出很好的预测，尤其适合于原始数据近似符合指数规律变化且变化速度不是很快的场合，但通常建立的灰色模型如常用的GM（1，1）模型处理的是等间隔时间序列，在其它时间序列预测模型中如移动平均法、指数平滑法等也要求数据为等间隔时间序列。然而，在某些问题的考察中，原始数据为非等间隔时间序列，本文就此问题作些探讨，对非等间隔时间序列分别为单调型和起伏型建立灰色模型。

1 不等间隔动态数据的灰色建模方法

1.1 单调型序列灰色建模

事物的发展大体上分为单调型和起伏型两大类，单调型是指事物随着时间呈递增态势，设单调型序列为不等间隔动态数据，记为其中为第ti年的数值，这里首先假定X(0)为非负递增型时间序列。

对X(0)进行一次累计计算，得生成序列：

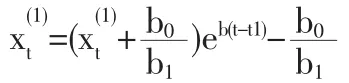
这是连续型微分方程模型，下面关键是估计出b0，b1为此需要进行离散化。这里设X(0)作一次累计。(1）式为

由差分和微分的关系

Δt+εt得

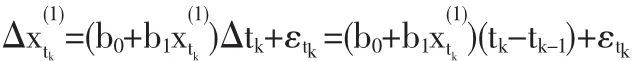
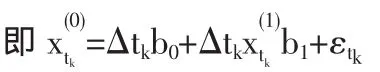
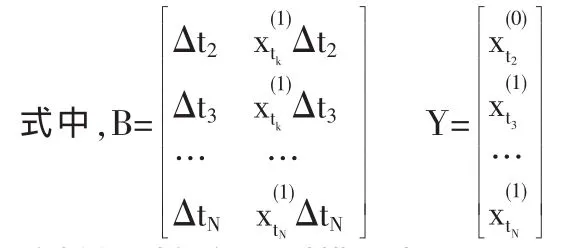
这样得到灰色预测模型为

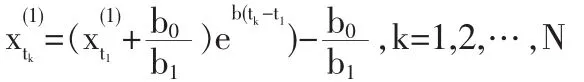
若序列是递增的，但其值是负的或开头的某些值是负的，则只要将数据作转换就得到一个非负的递增序列。若序列是递减的，则只要作转换就可得到递增序列，上式M为常数，按数据量级取某一值。

1.2 起伏型序列的灰色建模

若原始序列为不等间隔起伏型动态数据，在呈近似指数规律变化同时，还呈现周期性的波动。记原始序列为为第 ti年的数值。

对X(0)进行一次累计计算，得生成序列：

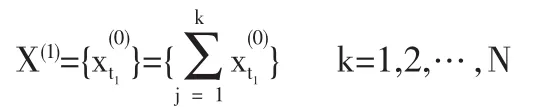
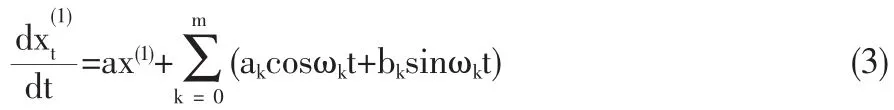
规定ω0=0，为求（3）式的解，我们先给出一般变系数线性微分方程设数据累加后X(1)满足微分方程的解.

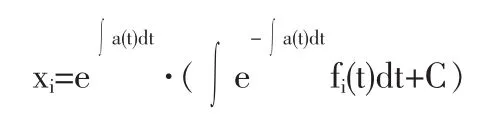
满足初值问题的特解为

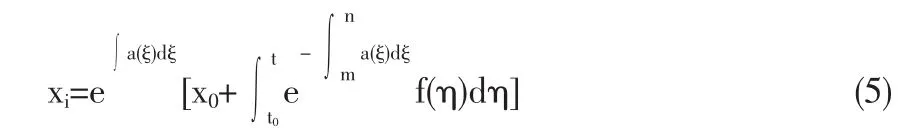
对（3）式，fi(t)=aicos(ωit)+bisin(ωit)

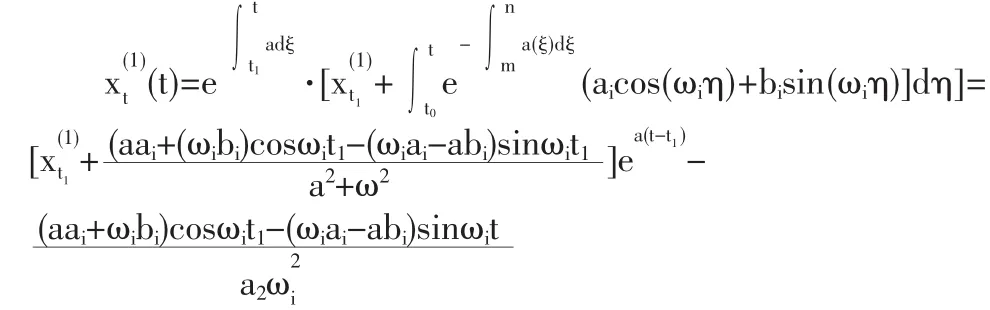
这样（3）式的解为

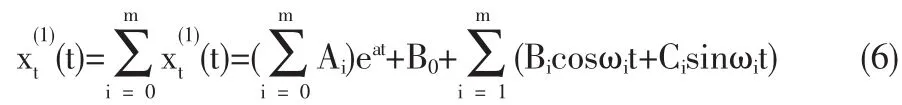
于是由

得到原始序列预测值。

现在需要对式（3）中未知变量 a、a0、a1、b1、a2、b2…am、bm、ω进行参数估计。这里给出线性化估计方法。先给出ωk的取值，N'为的 1≤N'≤N 某数值，可以通过多取几个值，建立模型后比较误差选取N'。

（3）式改写成

式中

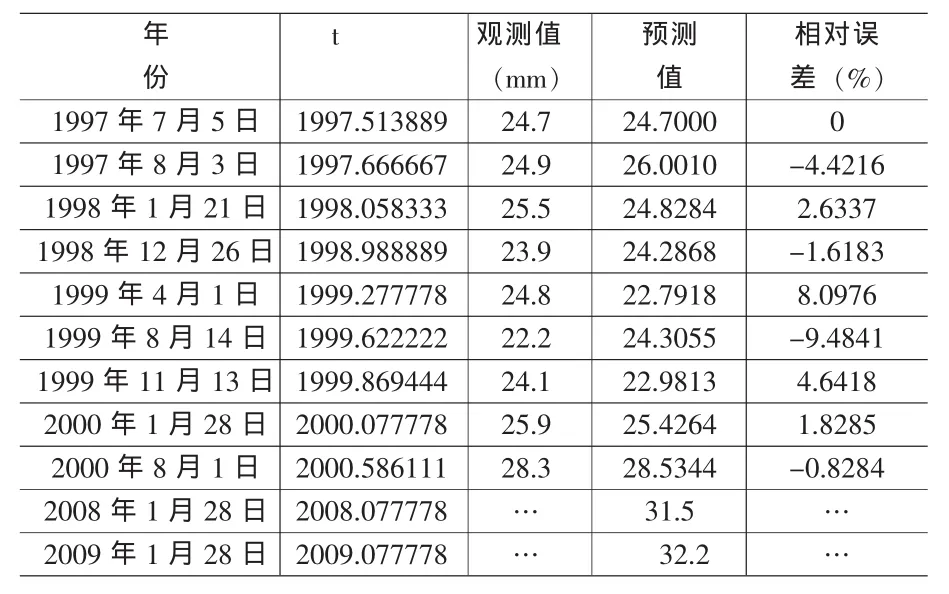
表1 苏州虎丘塔倾斜观测值及预测结果

这样求出 a、a0、a1、b1、a2、b2…am、bm

于是得到（6）式，再由得原始序列的估计值。

2 不等间隔动态数据的灰色建模应用于苏州虎丘塔倾斜预测

虎丘塔现有形变监测系统近年来建立,近年来对虎丘塔的监测一直在进行，积累了大量的观测数据。本文采用塔基加固以后的数据进行处理和分析，讨论虎丘塔维修以后至今塔体倾斜的发展趋势。由于第八层（最顶层）的形变量代表了虎丘塔的最大形变，是判断虎丘塔倾斜量的主要指标（见表1），这里就第八层的形变量进行预测，由于观测的数据是不等间隔时间序列，所以采用本文方法。

从表1中的数据可以看出时间序列在缓慢上升的同时，还存在季节性的变化（温度、雨量等季节性干扰）。

这里取 ωk=2πk/7(k=1,2,3，4)

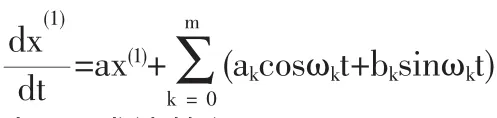
由（8）式计算得

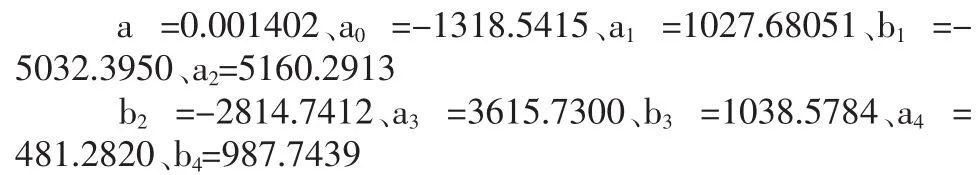
于是

[1]魏风英等.长期预测的数学模型及其应用[M].北京：气象出版社，1990.

[2]沈继红等.数学建模[M].哈尔滨：哈尔滨工程大学出版社，1996.

[3]邓聚龙.灰色控制系统[M].武汉：华中工学院出版社，1985.

[4]周纪芗.实用回归分析[M].上海：上海科学技术出版社,1990.

[5]刘则毅.科学计算技术与Matlab[M].北京：科学出版社，2001.

[6]程毛林.不等间隔动态数据的差分建模[J].数学认识,2003,(1).