农村社会救济效应的博弈均衡:理论分析及现实含义
2010-05-18周庆元
周庆元
(江苏技术师范学院,江苏 常州 213001)
0 引言
社会救济制度是政府通过二次分配的方式帮助穷人增加收入、维持最低生活、缩小收入差距的一种社会手段,其目的是维持正常的社会秩序,增进人民对社会的满意。救济制度的实施应该起到两个作用,即保障人民最低生活水平,增加社会福利水平和促进社会公平。我国是农业大国,农村救济制度具有极其重要的地位和作用。我国农村社会救济包括养老救济和贫困救济。养老救济主要是五保户制度,其救济范围小,周期固定,救济对象容易确定[1];而贫困救济则主要包括低保和不定期救济。农村低保制度处于起步阶段,贫穷地区还滞留在理论和资金的论战上。不定期救济金的发放,自新中国建立以来一直实行,并且,近年来随人民生活水平的上升,救济频度和救济金数额也在不断加大,但救济频度和救济金数额的加大并未完全达到预期的效果,这样做只是扩大了基层随意发放救济金的空间[2]。本文在设置假设体系的基础上建立农村社会救济效应的博弈模型,分析农村社会救济金发放后的效应及由此引起的基本矛盾,提出救济金发放的最优方案。目前,学术界对社会救济制度的研究很多,但涉及到农村的较少,研究的焦点都放在制度的完善[3]和发放的过程上[4],尚未涉及社会救济金发放后产生的效应,更没有从救济金发放后所产生的效应出发来研究救济制度,即现有的研究更关注怎么做,并未从深层次研究为什么这么做。忽视对社会救济效应的研究,可能产生的直接后果是不能设计推导出合理、科学的救济金发放制度。如果从社会道德的角度来说明实施救济制度的必要性和实施的方案是合理的,那么通过分析救济金发放后所产生的效应来说明救济金发放的必要性和最优实行方案是更合理的,这正是文章研究的焦点所在。本文在分析农村救济金发放后效应的基础上提出合理的救济金发放方案。
1 理论假设
1.1 模型假设
为了研究和说明问题的方便,本文建立以下假设体系:
(1)社会中只有两户村民甲、乙和一个政府,其中政府只决定社会救济金发放的对象 (村民甲乙得到救济金的概率,并不涉及政府的得益)。
(2)甲、乙获得救济金的概率分别为x、y,x与y的概率相互独立,其大小完全由救济金制度和政府对贫富的判断决定,其中 0≤x≤1,0≤y≤1。
(3)村民的得益完全反映的是村民对政府或社会的满意程度。村民对政府或社会的满意程度由两个因素决定:救济金对生活水平提高的弹性和发放救济金后村民之间对比产生的心理不平衡程度。
(4)当一户村民得到救济金,而另外一户没有得到救济金时,得到救济金的村民不会对比,不产生不平衡心理,没有得到救济金的一方产生不平衡心理。
(5)救济金的得益弹性是救济金变动的百分比引起村民得益变动的百分比。
1.2 经济行为假设
农村社会救济的不同发放组合所引起的政策效应大相径庭,根据不同组合及其对村民的影响作如下假设:
(1)村民生活没有保障,村民得到救济金且对比的结果没有不平衡时,救济金提高生活水平的弹性较大,获得救济金后的得益为5。
(2)村民生活没有保障,村民之间对比的结果存在不平衡时,产生不平衡的一方得益为-6。
(3)村民生活没有保障,且都没有社会救济金时,他们出于生活水平低下对社会有所不满,其得益为-1。
(4)村民生活水平较高,村民得到救济金且对比的结果没有不平衡时,因为社会救济金对生活水平提高的弹性不大,其得益为1。
(5)村民生活水平较高,村民没有得到救济金,即没有对社会不满意,也没有对比后产生的不平衡心理,其得益为0。
(6)村民生活水平较高,其中一户村民得到救济金时,产生不平衡心理村民的得益与得到救济金村民的得益相反,且绝对值相等。
(7)一户村民生活没有保障而另一户生活水平较高时,若生活水平较高的村民得到救济金而生活没有保障的村民却没有得到,则对比产生更加严重的不平衡,使得得到救济金的村民更加满意,其得益为2,而没有得到救济金的一方更加不满意,其得益为-8。
2 模型设计及理论分析
2.1 不同条件下的模型设计
由以上假设出发,根据甲乙两户村民是否存在生活差异和生活水平状况,区别设置三种状态,建立简单的博弈模型,并对此进行探讨。
(1)两户村民存在生活水平差异
甲乙两户村民存在生活水平差异,且甲生活没有保障,乙生活水平较高。其得益矩阵为:

甲的社会期望得益为:

乙的社会期望得益为:

整个社会的期望得益为:

(2)两户村民生活水平无差异,且生活水平较高
甲乙两户村民生活水平不存在差异,他们都处于贫困线上,生活水平较高。其得益矩阵为:

甲的社会期望得益为:

乙的社会期望得益为:

整个社会的期望得益为:
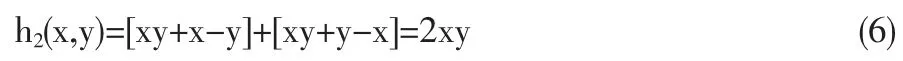
(3)两户村民生活水平无差异,且生活水平较低
甲乙两户村民生活水平不存在差异,他们都在贫困线以下,生活没有保障。其得益矩阵为:

甲的社会期望得益为:
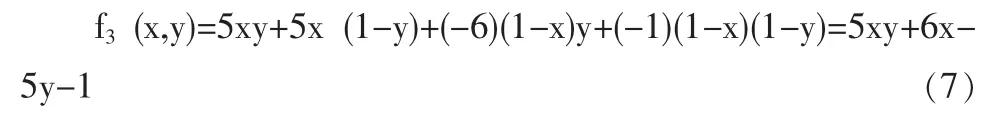
乙的社会期望得益为:

整个社会的期望得益为:

2.2 理论分析
为了使模型分析与模型设计初衷保持一致,对上述三种情况分别分析,具体分析如下:
第一种情况,对函数式(3)h1(x,y)=7xy+5x-5y-1求偏导得:

在定义域(0,1)上,h1(x,y)不存在极值点(x=5/7,y=-5/7),偏导数说明无论乙获得救济金的概率多大,甲的得益总是随救济金的增加而增大(7y+5>0)。但甲获得救济金的概率在区间[0,5/7]时,乙的偏导数的极限即乙获得救济金的概率不变时,其获得救济金后的得益随甲获得救济金的概率增大而增加,甲获得救济金的概率不变时,乙获得救济金后的得益随救济金数额的最大而减小。当甲得到救济金的概率在区间[5/7,1]时,其得益随救济金的增加而加速增大。这一现象说明富人希望维持当前的社会现状,不希望生活没有保障的穷人影响到自己的生活,但富人也会对穷人存在同情心,希望不损害自己利益的前提下改善穷人的生活水平。所以富人总希望政府通过救济金制度提高穷人生活水平。
第二种情况,对函数式(6)h2(x,y)=2xy求偏导得:

这表明无论他人获得救济金的情况如何,甲乙两各自获得救济金后的得益总是增大,对比方获得救济金的概率与自己得到救济金的的得益成正比关系。这说明村民生活水平都比较高且没有差异时,甲乙都很理性,甲认为乙得到比自己多的救济金后乙的心理更平衡,以更好地协调村民间的关系,乙也与甲存在同样的心理。而且由于h2(x,y)=2xy≤x2+y2,当且仅当x=y时h2(x,y)在救济金数额已定的条件下取得最大值。
第三种情况,对函数式(9)求偏导得:

由函数式(9)h3(x,y)=10xy+x+y-2的偏导数看以看出,第二种情况和第三种情况的有些类似,不同的是,这说明等量的救济金发给穷人的得益弹性大于发给富人的得益弹性。
3 研究结论及政策含义
3.1 研究结论
根据博弈模型的理论分析,并得到不同状态下的均衡解,可知最优发放救济金的基本结论:
(1)无论救济金发放给处于任何情况的村民,其个人的得益总是上升的。但因情况各异而救济金的得益弹性不同(增大速率不同),一般而言,随村民生活水平的提高,救济金的得益弹性呈递减趋势。
(2)两户村民生活水平没有差异的情况下,无论村民生活都处于较高水平还是生活没有保障,所有村民获得等量救济金时社会总得益最大,但随着村民生活水平从贫穷到富裕,其社会总得益的增速是递减的。
(3)两户村民生活水平存在差异的情况下,救济金的发放明显地倾斜向于生活水平较低的村民时,社会总得益更高。尽管富人没有得到救济金,但其得益至少不会下降,尤其是生活水平差异较大时,富人的得益也会上升。
3.2 政策含义
上述理论分析及其结论具有很强的现实含义,可以为我国农村社会救济政策的制定提供许多有意义的启示。
(1)要妥善解决农村社会救济存在的矛盾和问题,政府首先应从制度和基层政府的执行方面入手,规范社会救济金发放制度,完善相关法律法规,建立强有力的管理监督机制以保证救济金科学合理地发放,防范救济金以各种形式外流,保证救济金发放到位。
(2)其次,社会救济金发放的数额应随着人民生活水平的提高而有计划地减少[5],并逐渐地将社会救济金转化为农村基础设施建设的基金,创造农村经济社会发展的条件,以最大化资金效应,避免陷入低水平陷阱。
(3)再次,农村救济金的发放应明显地倾斜于生活水平低下的村民,而且应当明确标准,量化贫困要素,动态化评估村民家庭收入等级层次,有等级分层次地发放救济金,以最优化政策效果。
[1]郭孟谦.社会救济养老制度在农村的实施[J].中国青年政治学院学报,2004,(1).
[2]张俊武,陶恩前.对农村社会救济问题的几点思考[J].安徽农业通报,2006,(12).
[3]张鹏飞,张小华.完善中国社会救济法律制度的对策[J].社科纵横,2005,(12).
[4]苗永干.农村五保供养缺失救济的法理分析[J].河北农业科学,2008,(12).
[5]严仁丙.农村社会救济应实行贫困户等级化管理[J].中国民政,2001,(7).
