法向承力锚极限抗拔力影响因素的二维有限元分析

王 晖，董玉才，李新超，刘海笑，张 伟

(1. 天津大学建筑工程学院，天津 300072；2. 山东电力工程咨询院有限公司，济南 250013；3. 海洋石油工程股份有限公司，天津 300451)

法向承力锚极限抗拔力影响因素的二维有限元分析

王 晖1，董玉才2，李新超3，刘海笑1，张 伟1

(1. 天津大学建筑工程学院，天津 300072；2. 山东电力工程咨询院有限公司，济南 250013；3. 海洋石油工程股份有限公司，天津 300451)

法向承力锚(VLA)是一种新型深海工程系泊基础，锚板的极限抗拔力是反映其工作性能的主要指标.基于假设海底软黏土为符合Mises屈服准则的理想弹塑性材料以及锚板为一刚性体，采用大型有限元软件ABAQUS建立二维有限元模型，利用接触对模拟锚板与周围土体间的相互作用.从锚板粗糙程度、埋置深度、埋置角度、宽厚比以及荷载作用位置等多角度研究影响VLA极限抗拔力的因素及其影响规律.结果表明：当锚板埋深较小时，法向承载力系数随着锚板埋深和埋置角度增加而逐渐增大；当法向荷载作用在锚板形心处时其法向承载力系数大于法向荷载作用在非形心处时的法向承载力系数.

法向承力锚；极限抗拔力；法向承载力系数；锚-土接触面

近年来，随着海上石油、天然气等资源的开发从浅水域进入到深水域，大型柔性浮式结构代替传统的重力式结构，成为深海油气开采的必然趋势.法向承力锚(vertically loaded anchor，VLA)是一种新型深海工程系泊基础，由于其法向受力即系缆力作用方向垂直于锚板平面，因此与传统的拖曳嵌入锚和吸力锚相比具有高承载力特点，在工作状态 VLA受法向荷载作用时其极限抗拔力可以达到安装荷载的2.5～3.0倍[1]，是大型柔性浮式结构理想的系泊基础.极限抗拔力是反映VLA工作性能的主要指标，对其影响因素的研究具有重要应用意义.

Murrff和 Randolph等[2]研究了土体和锚板之间摩擦情况对锚板极限抗拔力的影响.O’nell等[3]利用二维有限元分析了楔形和矩形截面锚板的极限抗拔力.Taiebat等[4]对VLA在长期荷载下的极限抗拔力进行了研究.刘海笑等[1]基于土体塑性上限理论对锚板极限抗拔力进行了分析.Merifield等[5]通过建立二维有限元数值模型，利用极限分析理论研究了当锚板水平和竖直埋置时其极限抗拔力.Song等[6]运用小应变和大变形有限元分析方法对正常固结均质黏土中受法向载荷的条形、圆形平板锚进行了研究.Elkhartib等[7]在实验室中通过模型拖曳试验对 VLA的抗拔特性进行了研究.杨晓亮[8]基于土体塑性上限理论对锚板极限抗拔力进行了分析.刘君等[9]对饱和黏土中圆形锚板的极限抗拔力进行了分析.目前针对VLA极限抗拔力及其影响因素的研究较少，特别是国内尚处于起步阶段.为此，笔者利用大型通用有限元计算软件ABAQUS建立VLA和土体相互作用的二维有限元模型，从多角度研究 VLA极限抗拔力的影响因素，为适用于深海油气开发平台的新型系泊技术项目的模型试验研究提供参考和对比.

1 有限元数值模型

1.1 有限元数值模型的建立

矩形截面VLA锚板埋置如图1所示，图中：H为锚板埋置深度；nF为锚板极限抗拔力；B为锚板宽度；t为锚板厚度；α为锚板埋置角度.

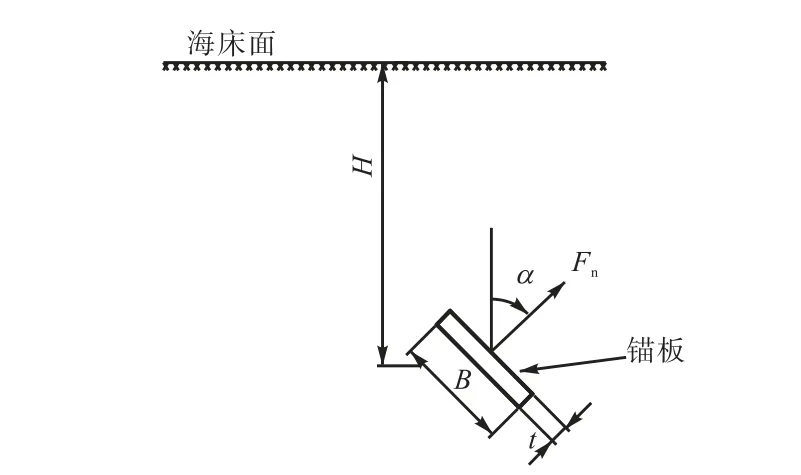
图1 VLA锚板埋置断面Fig.1 Section diagram of embedded VLA anchor

土体为海底软黏土，假设：①符合 Mises屈服准则的理想弹塑性材料；②土体不排水抗剪强度Su(kPa)在海床面处为零且随深度线性增大，即 Su＝1.5H；③土体弹性模量为不排水抗剪强度uS的 500倍，泊松比为0.49，Mises屈服应力sσ为u3S.

假设 VLA锚板为一刚性体，其弹性模量为土体弹性模量的107倍，泊松比为0.15.

采用有限元软件 ABAQUS建立二维有限元模型，其中锚板和土体均采用四边形双线性平面应变减缩积分单元 CPE4R.锚板和土体的接触面之间采用主-从接触算法建立接触对，锚板的表面取为主控表面，与其接触的土体表面取为从属表面.接触属性取为：①法向压力不受限制，出现拉力时两者会迅速脱开；②切向考虑锚板和土体之间的摩擦，摩擦属性定义为库仑摩擦，即

在锚板的上表面施加位移荷载，通过求解锚板与土体间的相互作用力来获得锚板的极限抗拔力.锚板周围土体区域除海床面外均施加垂直于土体边界的约束.图2所示为锚板埋置角度0α=时施加的位移荷载、土体边界条件示意图和有限元模型图.无特殊说明，以下分析中均取VLA锚板埋置角度0α=.

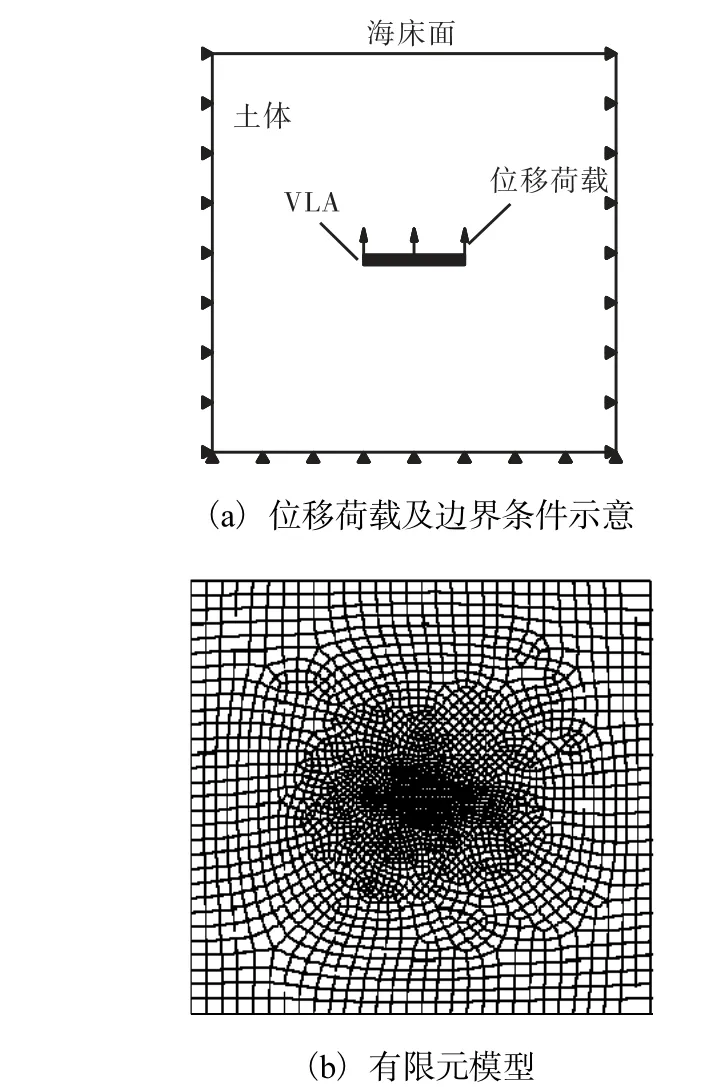
图2 二维模型Fig.2 Two-dimension model

1.2 锚板与土体接触模式

VLA 埋深 H＝25,m，锚板宽度B为 1.4,m，锚板厚度t为 0.2,m，对比分析 VLA在不同锚板与土体接触模式下的极限抗拔力.模型1采用小滑移接触方式，即假设锚板与土体接触面间有很小的相对滑动，但两者接触位置仍保持不变.模型2采用有限滑移接触方式，即假设锚板与土体接触面间可以有任意的滑动，两者接触位置可以变化.模型3采用黏结方式即假设锚板与土体接触面始终没有分离和相对滑动.

图3为不同接触模式下VLA锚板抗拔力F随着法向位移荷载的变化情况.可以看出，随着位移荷载的增加，锚板抗拔力F逐渐增大，直到达到其极限值.在小滑移和黏结模式下，锚板在较小位移荷载时，已经达到其极限抗拔力，分别为634.6,kN/m和685.2,kN/m；在有限滑移方式下，当位移荷载为0.14,m 时，锚板抗拔力趋于小滑移情况的极限抗拔力.由图3可见，按黏结条件处理方式计算出的极限抗拔力大于按接触条件处理方式的计算值，由于锚板在实际极限受力状态下与土体是分离的，所以如无特殊说明，以下分析中均取小滑移接触方式进行计算.

图3 不同接触模式下F-位移荷载曲线Fig.3 F-displacement load curves of different interaction Fig. 3 modes

1.3 土体性质

VLA 锚板宽 3,m，厚度为 0.2,m；土体区域取60,m×60,m，不同土体模型的参数见表1.

表1 不同土体的参数Tab.1 Parameters of different soils

表1中为4种不同的土体，其中土体1分别采用M-C模型和D-P模型进行模拟，M-C理想弹塑性模型参数和D-P模型参数之间的转换为

式中：d、β分别为 D-P模型中材料的黏聚力、内摩擦角；c、φ分别为 M-C模型中材料的黏聚力、内摩擦角.

土体2用M-C模型和Mises理想弹塑性模型模拟，土体3和土体4用Mises理想弹塑性模型模拟.

由图4和图5可以看出，相同土体采用不同土体模型时，计算出的锚板抗拔力 F-位移荷载曲线基本一致，说明土体模型选取对锚板极限抗拔力的影响很小.由图 6可见，虽然土体 3和土体 4土性不同，但由于在锚板处具有相同的屈服强度，计算出的 F-位移荷载曲线基本一致，这说明锚板极限抗拔力仅与锚板周围的土体强度有关.本文中以下计算土体均采用Mises理想弹塑性模型模拟.

图4 土体1的F-位移荷载曲线Fig.4 F-displacement load curves of soil 1

图5 土体2的F-位移荷载曲线Fig.5 F-isplacement load curves of soil 2

图6 土体3和土体4 的F-位移荷载曲线Fig.6 F-displacement load curves of soil 3 and soil 4

2 锚板极限抗拔力的影响因素

法向承载力系数cN是衡量 VLA极限抗拔力的重要指标，其表达式为

式中：nF为锚板的极限抗拔力；B为锚板的宽度；uS为锚板周围土体的不排水抗剪强度.

2.1 锚板粗糙程度

通过对埋深分别为25,m和2,m的VLA计算分析，研究锚板的粗糙程度对极限抗拔力的影响.锚板宽度 1.4,m，厚度 0.2,m，土体区域 60 m×60,m，数值模型中土体的参数见表 2.锚板粗糙程度可通过锚板与土体之间的摩擦系数μ(01μ≤≤)来度量.

表2 土体参数(Ⅰ)Tab.2 Soil parameters (Ⅰ)

由图 7可见，文献[2]采用有限元法计算了宽厚比为 7、不同摩擦系数时 VLA 的极限抗拔力.在摩擦系数为 0时，本文计算结果和文献[2]计算结果分别为11.15和11.29，两者相差1.2%；在摩擦系数为1时，本文计算结果和文献[2]的计算结果分别为 11.49和 12.09，两者相差4.9%.由此可见，本文有限元计算结果与文献[2]的计算结果基本一致.

由图7和图8可以看出，埋深25,m时，极限承载力系数由0μ=时的11.15增大到1μ=时的11.49，增加了3.0%；埋深2 m时，极限承载力系数由0μ=时的2.81增大到1μ=时的2.88，增加了2.4%.随着锚板粗糙程度加大即摩擦系数增大，VLA极限抗拔力系数随之仅有略微增大.由此可得：锚板粗糙程度对极限抗拔力系数影响较小.以下无特别说明，则分析中取摩擦系数为1.

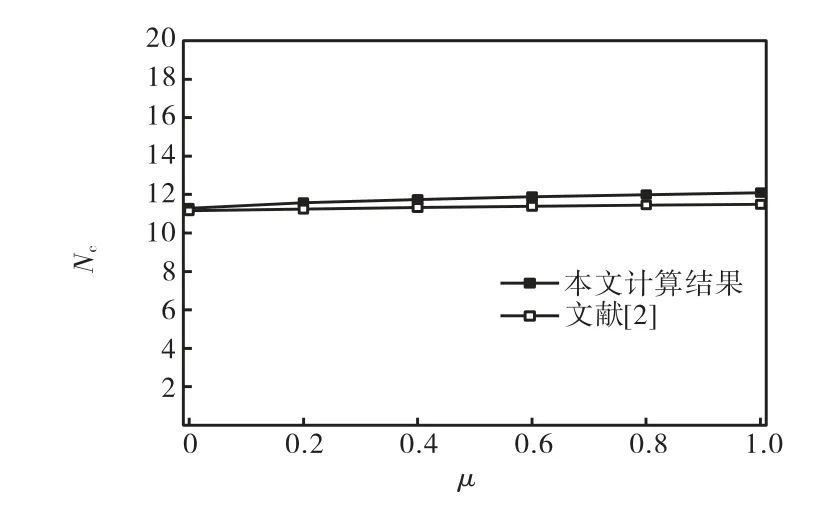
图7 埋深25 m cN-μ曲线Fig.7 cN-μ curves of anchor embedded in 25 m

图8 埋深2 m N c-μ曲线Fig.8 Nc-μ curve of anchor embedded in 2 m

2.2 锚板埋置深度

VLA 锚板宽 3,m，厚度为 0.2,m，土体区域为60,m×60,m.土体弹性模量为 2,250,kPa，不排水抗剪强度为4.5,kPa.研究当锚板宽度B一定时，不同锚板埋置深度H对极限抗拔力的影响.

图 9为不同埋深情况下锚板抗拔力F-位移荷载曲线，可以看出VLA极限抗拔力随埋深增加而增大.

图10为极限抗拔力Fn随埋深变化曲线，可以看出，当 H/B＜7，即 H＜7B时，随着锚板埋深的增加，极限抗拔力 Fn逐渐增大.当 7＜H/B＜8，即 7B＜H＜8B 时，Nc将迅速增大，产生突变.当 H/B＞8，即 H＞8B时，Fn逐渐趋于定值.

图9 F-位移荷载曲线Fig.9 F-displacement load curves

图10 Fn-H/B曲线Fig.10 Fn-H/B curve

图11将有限元结果和 Merifield[10]、O’Neill[3]的求解结果进行了比较.对比本文有限元解和 Merifield的结果可以看出，在埋深较小时，两者差别不大，在埋深较大时，后者没有反应出深埋破坏的特征.对比本文有限元解和O’Neill深埋时解，在H＝10B时，本文计算出的Nc值为11.94和O’Neill给出的深埋情况下的上限解12.10相差1.32%.

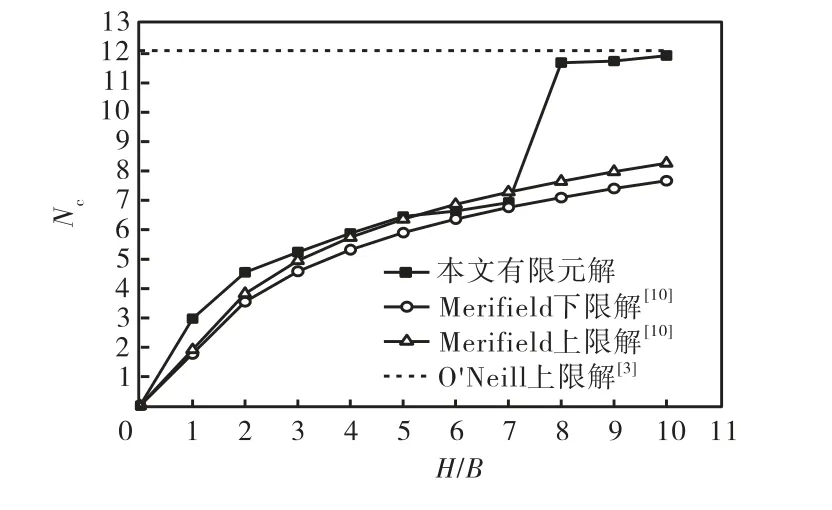
图11 法向承载力系数 cN-H/B曲线Fig.11 Normal bearing capacity factor cN-H/B curves

2.3 锚板埋置角度

研究埋深一定时，VLA锚板的埋置角度α与极限抗拔力的关系.锚板宽 1.4,m，厚度 0.2,m，土体区域取 60,m×60,m.锚板埋置深度分别取 4,m 和25,m，土体的参数见表3.

表3 土体参数(Ⅱ)Tab.3 Soil parameters(Ⅱ)

图12和图13分别为埋深4,m和25,m时，法向承载力系数与锚板埋置角度的关系曲线.当锚板埋置角度α由 0°增大到 90°时，埋深 4,m时，极限承载力系数Nc由5.1增加到8.5；埋深25,m时，法向承载力系数在12.2～12.3之间变化，最大值和最小值仅相差 0.8%.得出结论：在埋深较小时，VLA的极限承载力系数 Nc随着锚板埋置角度的增大而增大；在埋深较大时，锚板的埋置角度对极限承载力系数 Nc影响不大.

图12 埋深4 m cN-α曲线Fig.12 cN-α curve of anchor embedded in 4 m

图13 埋深25 m cN-α曲线Fig.13 cN-α curve of anchor embedded in 25 m

2.4 锚板宽厚比

VLA锚板宽度B一定，改变锚板的厚度t，考察锚板宽厚比对VLA极限抗拔力的影响.锚板宽3,m，埋深 25,m，土体区域取 60,m×60,m.土体弹性模量为17.85,MPa，抗剪强度uS 为37.5,kPa.

由图 14可以看出，在埋深 25,m的情况下，VLA的极限抗拔力系数随着宽厚比的增大而略有减小.O’Neill[3]利用极限分析的方法，给出了在完全粗糙锚板的理论解.由图14中可见，当锚板宽厚比 B/t大于7时，两者计算的结果基本一致.

图14 cN- B/t曲线Fig.14 cN-B/t curves

2.5 任意荷载作用

VLA锚板宽3.5,m，厚度0.5,m，埋深30,m，土体弹性模量为22.5,MPa，抗剪强度uS为45,kPa.当一非法向力 T作用于锚板任意一点 A处时，可将该力分解为作用在锚板形心上的沿法向和切向的力 fn和 fs及外力偶fm，如图15所示.

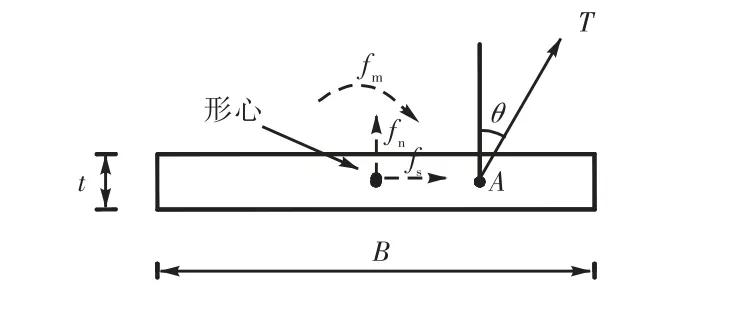
图15 荷载示意Fig.15 Loads of anchor

锚板在承受切向力或外力偶时，其承载力性能用切向承载力系数和弯曲承载力系数表示为

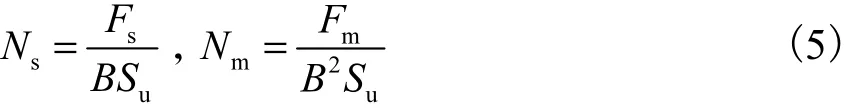
式中：sF为锚板的切向极限剪力； fm为锚板的极限弯矩.

通过在锚板形心上施加法向位移荷载vδ、切向位移荷载hδ和转角荷载βδ，研究任意荷载作用下极限抗拔力的变化情况.在锚板上施加法向位移vδ和切向位移hδ，得到如图16所示的锚板Nc-Ns破坏曲线；施加法向位移vδ和转角βδ，得到如图17所示的锚板Nc-Nm破坏曲线；图18为施加切向位移hδ和转角βδ时，锚板的Ns-Nm破坏曲线.

从图16～图18可知，任意荷载作用下锚板的屈服轨迹较为复杂.图 16中，在 Nc-Ns屈服空间中，随着hδ/δv位移比的增大，法向承载力系数Nc急剧降低，切向承载力系数Ns逐渐增大；当βδ＝0、hδ＝0，即仅有作用在锚板形心处的法向力，Nc达到最大值12.02.图17中，在Nc-Nm屈服空间中，随着βδ/vδ位移比的增大，法向承载力系数 Nc急剧降低，弯曲承载力系数 Nm逐渐增大；当δv＝0、δh＝0，即仅有作用在锚板形心处的外力偶，Nm达到最大值为 1.95.图18中，在Ns-Nm屈服空间中，随着βδ/hδ位移比的增大，切向承载力系数 Ns急剧降低，弯曲承载力系数Nm逐渐增大；当vδ＝0、βδ＝0即仅有作用在锚板形心处的切向力，Ns达到最大值为3.43.

图16 Nc-Ns曲线Fig.16 Nc-Ns curve

图17 Nc-Nm曲线Fig.17 Nc-Nm curve

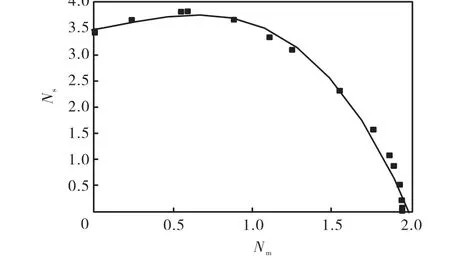
图18 Ns-Nm曲线Fig.18 Ns-Nm curve

3 结 论

利用 ABAQUS软件建立了VLA和土体相互作用的二维有限元数值模型，并对极限抗拔力影响因素进行了系统分析，得到如下结论：

(1) 土体数值模型的选择对极限抗拔力的计算结果影响很小.

(2) 锚板粗糙程度(摩擦系数)对极限抗拔力影响较小.

(3) 当锚板埋深较小时，法向承载力系数 Nc随埋深增加而逐渐增大；当锚板埋深较大时，Nc趋于定值不随埋深增加而增大.

(4) 当锚板埋深较小时，法向承载力系数 Nc随锚板埋置角度的增大而增大；当锚板埋深较大时，锚板的埋置角度对Nc影响不大.

(5) 法向承载力系数 Nc随着锚板宽厚比 B/t的增大而略有减小.

(6) 当锚板在任意荷载作用下，屈服轨迹较为复杂.单向受力状态下，法向承载力系数cN、切向承载力系数sN和弯曲承载力系数mN分别都取得最大值；在复合荷载作用下，承载力系数有所降低.对于在法向荷载作用下的锚板其法向承载力系数大于法向荷载作用在锚板非形心处时的法向承载力系数.

［1］刘海笑，杨晓亮. 法向承力锚极限抗拔力特性[J]. 海洋工程，2005，24(4)：8-14.

Liu Haixiao，Yang Xiaoliang.Characteristics of ultimate pull-out capacity for vertically loaded anchor[J].The Ocean Engineering，2005，24(4)：8-14(in Chinese).

［2］Murff J D，Randolph M F，Elkhaib S，et al. Vertically loaded plate anchors for deepwater applications[C]//Frontiers in Offshore Geotechnics. Taylor and Francis，London，UK，2005：31-48.

［3］O’Neill M P，Bransby M F，Randolph M F. Drag anchor fluke-soil interaction in clays[J].Canadian Geotechnical Journal，2003，40(1)：78-94.

［4］Taiebat H A，Thorne C P，Carter J P. Effects of long term loading on storm capacity of vertically loaded anchors[C]//Frontiers in Offshore Geotechnics. Taylor and Francis，London，UK，2005：191-196.

［5］Merifield R S，Lyamin A V，Sloan S W.Stability of inclined strip anchors in purely cohesive soil [J].Journal of Geotechnical and Geoenvironmental Engineering，2005，131(3)：792-799.

［6］Song Zhenhe，Hu Yuxia，Randolph M F.Numerical simulation of vertical pullout of plate anchors in clay[J].Journal of Geotechnical and Geoenvironmental Engineering，2008，134(6)：866-875.

［7］Elkhatib S，Lonnie B，Randolph M F. Installation and pull-out capacities of drag-in plate anchors[C]//Proceedings of the12th International Offshore and Polar Engineering Conference. Kitakyushu，Japan，2002：26-31.

［8］杨晓亮.法向承力锚的极限抗拔力研究[D]. 天津：天津大学建筑工程学院，2005.

Yang Xiaoliang. Research on the ultimate pull-out capacity of the vertically loaded anchor(VLA)[D]. Tianjin：School of Civil Engineering，Tianjin University，2005(in Chinese).

［9］刘 君，吴利玲，孔宪京. 成层地基中圆形锚板的抗拔承载力[C]// 第 2届全球华人岩土工程论坛文集.南京，2005：201-207.

Liu Jun，Wu Liling，Kong Xianjin. Pullout capacity of circular plate anchor in stratified clays[C]//Proceedings of the 2nd Global Chinese Geotechnology Engineering Forum. Nanjing，China，2005：201-207(in Chinese).

［10］Merifield R S，Lyamin A V，Sloan S W，et al. Threedimensional lower bound solutions for stability of plate anchors in clay[J].Journal of Geotechnical and Geoenvironmental Engineering，2003，129(3)：243-253.

Two-Dimensional FEM Analysis of Influencing Factors on Ultimate Pull-Out Capacity of Vertically Loaded Anchor

WANG Hui1，DONG Yu-cai2，LI Xin-chao3，LIU Hai-xiao1，ZHANG Wei1
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Shandong Electric Power Engineering Consulting Company Limited，Jinan 250013，China；3. Offshore Oil Engineering Company Limited，Tianjin 300451，China)

Vertically loaded anchor(VLA)is a new type of mooring foundation for deep-water offshore engineering.The ultimate pull-out capacity of anchor plate is an important working performance parameter. Based on the assumption that submarine soft soil around anchor plate is an elastic-perfectly plastic material which obeys Mises yield condition，and the anchor plate is a rigid body，the two-dimensional finite element model is established by use of the finite element analysis software ABAQUS and the anchor-soil interaction is simulated by the contact pair. Moreover，many influencing factors including roughness，embedment depth，inclination angle，aspect ratio，and load positionof anchor plate are considered to analyze the ultimate pull-out capacity of VLA. It’s found that at a shallow embedment depth，the normal bearing capacity factor increases with increasing embedment depth and inclination angle of the anchor. The normal bearing capacity factor which normal load acts on anchor’s centroid of area is larger than that the load is not at the centroid of area.

vertically loaded anchor；ultimate pull-out capacity；normal bearing capacity factor；anchor-soil interface

TV223

A

0493-2137(2010)11-0964-07

2009-03-19；

2010-01-12.

国家高技术研究发展计划(863计划)资助项目(2006AA09Z348).

王 晖（1968— ），女，博士，副教授.

王 晖，hollywanghui@hotmail.com.