S变换数值计算方法比较的实验研究

刘保童, 刘启源, 吴玉林



S变换数值计算方法比较的实验研究

刘保童, 刘启源, 吴玉林

(天水师范学院 物理与信息科学学院, 甘肃 天水, 741000)

为了对S变换的不同实现方法进行比较, 在MatLab环境下采用数值计算实验的方法, 展现了数值实现S变换的不同方法中存在的误差及滤波效果的区别, 为S变换这一工具的合理应用提供了有益的参考. 研究表明, 频率S变换(fST)与频率反S变换(fIST)结合, 时间S变换(tST)与时间反S变换(tIST)结合, 是2种可在实际中使用的方法, 它们各有优势与不足.

S变换; 时-频分析; 滤波器; 重建误差

S变换(S transform, ST)[1]是短时傅里叶变换和连续小波变换思想的延伸或推广, 其分辨率是依赖于频率的. 在S变换中, 窗函数是一个可随频率的变化而伸缩的高斯(Gaussian)函数, 在高频处有较窄的窗, 在低频处有较宽的窗. S变换具有连续小波变换所没有的一些优点, 并与傅里叶谱保持直接的联系, 已在不同应用中发挥积极作用. 例如, 文献[2]将S变换用于心电图分析, 文献[3]利用S变换分析了齿轮振动信号, 文献[4-5]是S变换在地球物理信号处理中的应用. 另外还有许多作者对S变换的应用进行了有益地探索. 如何将S变换成功用于各种实际问题, 近年来受到有关研究人员的重视.

Stockwell等人提出S变换的数值实现方法有2种, 反S变换(inverse S transform, IST)有1种[1]. 近年来关于S变换的研究取得了一个新进展, 文献[6]提出了1种新的时间反S变换(time IST, tIST), 于是, S变换的数值实现方法有2种, S反变换的数值实现方法也有两种. 不同形式的S变换与S反变换有何区别, 正、反变换怎么结合, 是值得研究的问题, 对S变换的应用有重要意义. 文章通过数值计算实验的方法, 对数值实现S变换及其反变换的不同方法进行了比较与分析, 得到了一些有意义的结论. 本文行文如下：首先回顾了S变换与反变换的理论基础, 接着给出离散计算公式. 然后, 通过数值计算实验, 对各种实现S变换及其反变换的方法进行了比较分析, 最后给出几点研究结论.

1 S变换与反变换理论基础

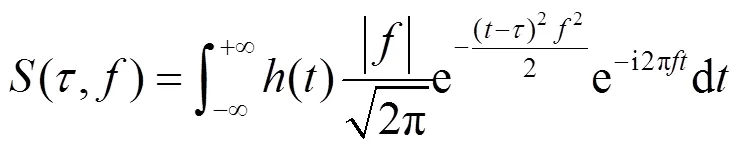
这种写法的S变换我们称为频率S变换(frequency ST, fST), 而另一种写法(1)将称为时间S变换(time ST, tST).

S变换的良好性质之一在于它是完全可逆的. 由于在时间上求和得到函数的傅里叶谱:

我们称(4)式为频率反S变换(frequency IST, fIST). 近年来, Schimmel等人[6]提出了一种新的反S变换：时间反S变换(time IST, tIST). 对函数()加窗可定义下面的函数集:

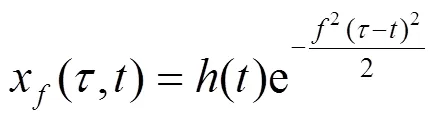
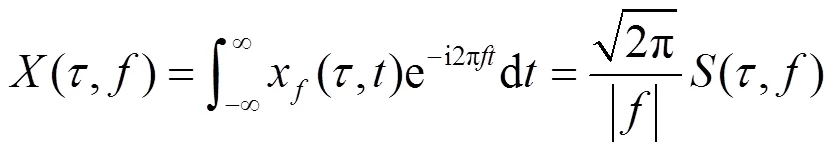
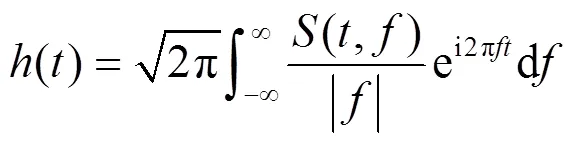
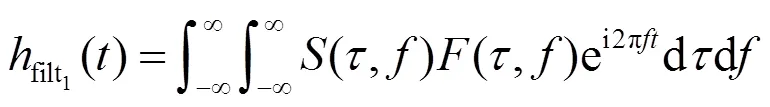
2 在离散情况下S变换及其反变换的计算

频率S变换(2)的离散计算式为:

时间反S变换(8)的离散计算式为:

3 数值计算实验

3.1 两种S变换的差别

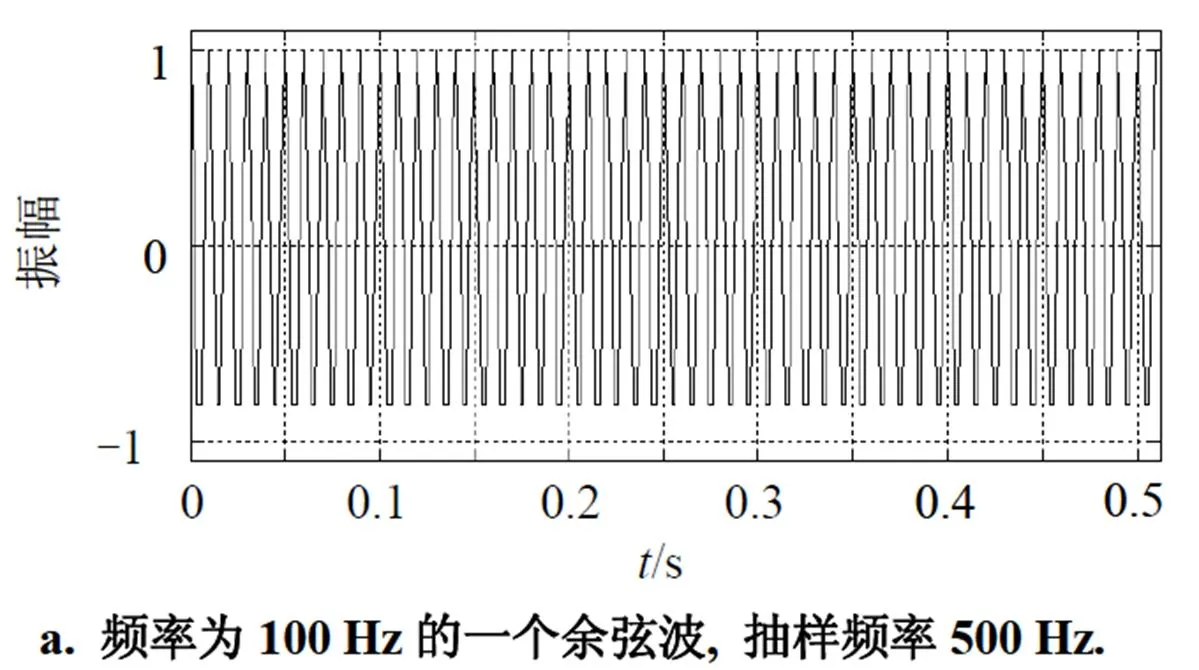
设有一个频率为100 Hz的余弦波, 单位振幅, 持续长度0.256 s, 时间采样率0.002 s, 见图1(a). 用时间S变换(11)计算的时频谱见图1(b), 用频率S变换(12)计算的时频谱见图1(c), 二者的幅度差显示在图1(d)中. 可见, 虽然在无限连续情况下, 时间S变换(1)与频率S变换(2)是等价的, 但在有限离散的情况下, 用(11)和(12)数值计算得到的变换结果是有差别的, 主要表现在左、右两侧的边界附近, 且愈靠近边界差别愈大, 这与文献[7]的理论分析结果是一致的.

3.2 重建误差

图2(a)是一个单色波(), 与图1(a)相比只是长度不同.()做fST后, 对时-频谱不做任何改动(相当于=1), 直接做tIST返回到时间域, 重建结果与原信号()的差在图2(b)中用细实线表示, 存在低频误差, 总重建误差小于原信号最大振幅的5％；而直接做fIST返回到时间域时, 重建结果与原信号()的差在图2(b)中用粗短划线表示, 误差处处为零.()做tST后, 对时-频谱不做任何改动(相当于=1), 直接做tIST返回到时间域, 重建结果与原信号()的差在图2(c)中用细实线表示, 不存在低频误差, 总重建误差也小于原信号最大振幅的5％；而直接做fIST返回到时间域时, 重建结果与原信号()的差在图2(c)中用粗短划线表示, 中间0.05～0.47 s的区间误差接近于零, 但在两侧边界附近误差太大, 故图2(c)采用双坐标图, 细线型坐标轴控制细实线, 粗线型坐标轴控制粗短划线.

可以看出：a. fST与fIST结合, 重建精度最高, 误差为零；b. fST与tIST结合, 存在低频误差, 但总重建误差占原信号最大振幅的百分之几; c. tST与tIST结合, 无低频误差, 总重建误差也占原信号最大振幅的百分之几; d. tST与fIST结合, 两端边界附近误差太大.

鉴于b、c两种情况的总误差相当, 为说明在滤波中tIST比fIST的优势, 便于比较, 下面只就fST的情况进行数值实验.

3.3 滤波效果比较

4 结论

通过数值实验研究, 得到如下结论:

a. 时间S变换(tST)与频率S变换(fST)的离散数值计算结果是不同的, 差异在两侧边界附近；

b. S变换与反变换各种形式的不同组合, 产生的重建误差不同；

c. 频率反S变换(fIST)使滤波器的时间局部化特征受到损失；

d. 时间反S变换(tIST)保持了滤波器中的时间局部特征, 避免了时频滤波中能量扩散造成的假信号；

e. 时间反S变换(tIST)是一种近似方法, 总误差最大值为原始信号最大振幅的百分之几；

f. 频率S变换(fST)与频率反S变换(fIST)结合, 时间S变换(tST)与时间反S变换(tIST)结合, 是2种可在实际中使用的方法, 它们各有优势与不足. 频率方法与时间方法不宜交叉混合使用.

[1] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions On Signal Processing, 1996, 44(4): 998- 1001.

[2] Livanos G, Ranganathan N, Jang J. Heart sound analysis using the S transform[J]. Computers in Cardiology, 2000, 27: 587-590.

[3] McFadden P D, Cook J G, Forster L M. Decomposition of gear vibration signals by the generalized S transform[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 691-707.

[4] Pinnegar C R, Mansinha L. The S-transform with wind- ows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385.

[5] Parolai S. Denoising of seismograms using the S trans- form[J]. Bulletin of the Seismological Society of America, 2009, 99(1): 226-234.

[6] Schimmel M, Gallart J. The inverse S transform in filters with time-frequency localization[J]. IEEE Transactions On Signal Processing, 2005, 53(11): 4417-4422.

[7] Simon C, Ventosa S, Schimmel M, et al. The S-transform and its inverses: side effects of discretizing and filtering [J]. IEEE Transactions On Signal Processing, 2007, 55(10): 4928-4937.

Experimental researches on comparison of S transform numerical methods

LIU Bao-tong, LIU Qi-yuan, WU Yu-lin

(College of Physics and Information Science, Tianshui Normal University, Tianshui 741000, China)

In order to compare different numerical methods of S transform, this paper illustrates errors and filtering effects of different procedures via computing experiments under MatLab environment, provides useful references. The research showed, frequency S transform in conjunction with frequency inverse S transform and time S transform in conjunction with time inverse S transform are two practical methods, each of them has its advantages and disadvantages.

S transform; time-frequency analysis; filter; reconstruction error

TN 911.7

A

1672-6146(2010)03-0016-04

10.3969/j.issn.1672-6146.2010.03.007

2010-06-07

甘肃省教育厅科研项目(0908B-1)

刘保童(1965-), 男, 副教授, 博士, 研究方向为数字信号处理、数学物理方法和大学物理.