基于变窗函数方法的频率检测技术研究

文超斌，李世平，刘如峰，宋 兵

（第二炮兵工程学院，陕西 西安 710025）

1 引 言

获取信号频率作为信号分析的主要内容之一，在工程应用中占有很重要的地位。目前国内外对多频信号通过频谱校正进行精确测量的方法很多，如比值校正法，相位差校正法等[1-6]。这些方法对解析单频信号或频率成分间隔较大的情景都具有优良的特性，但由于没有考虑负频谱的影响，所以应用在正负频谱发生严重干涉的低频信号谱中时，其校正精度明显下降，甚至失去校正作用。

频率的高低与记录的长短有关，信号频率的高低是相对的概念，如果分析样本内含有足够多的波动周期数则可视为高频，这时就可以忽略负频谱的影响。然而在很多种情形下，采集样本可能不满足这个条件，例如工程实践中往往要进行信号实时处理从而要求被处理信号足够短。另外，很多情况下已采集到的数据不够长，但再次采集成本又很高，这时信号正负频谱发生了严重的干涉，常用校正方法将达不到精度的要求，甚至不能使用。因此，有必要进一步研究建立系统的考虑负频响应的高精度多频率测量技术，文献[3-5]给出了考虑负频谱影响的几种方法，但是这些方法的测频精度受信号中直流分量的影响较大。该文在考虑负频响应的情况下建立信号频谱模型，多个窗函数组合应用，总结出一套显式测频的新方法。仿真结果表明，这个方法比简单比值法精度更高、应用范围更广、实用性更强。

2 考虑负频响应的频谱模型

带直流偏移的正弦波模型x（t）如下：

式中：f0、A、φ0和B——信号的频率、幅值、初相位和直流偏移量4个参数。

假定式（1）在[0，T]上截断。采样样本内包含的信号周期个数可简记为 CiR（Cycles in Record）[5]，其值等于f0与Δf的比，其中Δf表示信号FFT变换频谱的频率分辨。设w（t）为定义在区间[-T/2，T/2]上的对称窗函数，其频域表达式为W（f），把该窗函数平移至区间[0，T]得窗函数wT（t）。用窗函数wT（t）对正弦波模型信号x（t）进行截断得截断信号xT（t）。则该截断信号的傅里叶变换频谱函数XT（f）为频率f的连续函数，即：

由傅里叶变换时移特性有：

所以由式（2）、式（3）、式（4）并且结合傅里叶变换频移特性有：

3 算法推导

考虑式（5）截断信号的傅里叶变换频谱函数XT（f）在零频率处的频谱值为：

用任意3个对称窗函数如上面叙述操作：分别平移后对正弦波信号模型x（t）截断，并且分别求出其对应的3个傅里叶变换频谱函数XTi（f），考虑函数XTi（f）在零频率处的频谱值，记为XTi（0）（其中i=1，2，3）。

构造运算：

并且记：

研究发现，若利用窗函数幅值恢复系数在FFT变换前对所涉及到的窗函数自身进行补偿，确保截断信号的傅里叶变换频谱函数对应频谱在零频率处幅值相等，这样式（7）构造的运算：做差消去了直流分量对测频精度的影响；相除可使式（7）右边运算中涉及到的复杂非线性部分对消，最终得到关于要求频率的函数。

算例1：取窗函数1，2，3进行研究，利用各自窗函数幅值恢复系数对自身进行补偿。

将式（9）3个新的窗函数分别代入式（6），求出此3个新的窗函数分别由区间[-T/2，T/2]平移至区间[0，T]，而后对正弦波信号模型 x（t）进行截断，所得3个不同截断信号的傅里叶变换频谱函数在零频率处的频谱值：

其中 i=1，2，3，于是由式（9）、式（10）并且结合式（7）构造运算得：

整理可得：

另外，对正弦波截断信号xT（t）进行采样得离散信号xT（n），该离散信号进行FFT变换可得截断信号xT（t）对应的离散频谱在频率fi处的频谱值为：

（其中 i=0，1，2，3，…，N）可见由计算机对采样信号做FFT变换可直接求出信号离散频谱在零频率处的频谱值，而这正是前面叙述中截断信号的傅里叶变换频谱函数XT（f）在零频率处的频谱值XT（0）。于是利用式（9）中经过补偿的3个窗函数分别对正弦波模型信号x（t）截断，采样得其对应的离散信号，而后进行FFT变换可得到3个不同截断信号的傅里叶变换频谱函数XTi（f）在零频率处的频谱值XTi（0）（其中i=1，2，3），进而由式（8）可求出K。这样由式（11）即可以解出正弦波信号的频率f0：

当W1（f）=Wr（f），W2（f）=ahnWhn（f），

W3（f）=abWb（f）时，同理得：

当W1（f）=Wr（f），W2（f）=abWb（f），

W3（f）=ahnWhn（f）时，同理得：

算例2：取窗函数2，3，4进行研究时，同样方法可得对应于3种窗函数不同的组合顺序频率计算公式分别为：

算例3：取窗函数1，3，4进行研究时，同样方法可得对应于3种窗函数不同的组合顺序频率计算公式分别为：

4 仿真研究与结果讨论

4.1 仿真参数与计算条件

按照式（1）正弦波信号模型生成原始数据，这里只考虑无噪声干扰的情形。信号直流偏移量B=1V，幅值A=1V，初相位φ0=0。采样样本大小N=2000，采样频率fS=50000Hz，信号FFT变换频谱的频率分辨Δf=fS/N=25Hz。

为全面反映该文所述新方法测频的效能，这里用以上总结出的各个测频计算公式，分别在信号频率变动化时，求出各个仿真信号的频率归一化绝对误差，并绘出了相应的曲线图，被测低频信号频率f0从0.1Δf扫描到10Δf，扫描步长为0.1Δf（电网中的谐波频率变化通常为45～55 Hz对应这里为频率f0从1.8Δf扫描到2.2Δf[7-9]）。也就是仿真信号采样样本内包含的信号周期个数CiR从0.1线性增加到10，步长为 0.1。

图1～图3中给出了以上算法推导部分3种不同的算例情况，分别用各自算例3个不同公式计算频率的归一化绝对误差曲线。第一个算例（图1）取窗函数 1，2，3，分别用式（11）、式（13）、式（14）进行计算；第二个算例（图2）取窗函数2，3，4分别用式（15）、式（16）、式（17）进行计算；第三个算例（图 3）取窗函数 1，3，4 分别用式（18）、式（19）、式（20）进行计算；图4画出了当CiR在区间0.5～2.67变化，步长变为 0.02Δf，取窗函数 1，2，3（算例 1）时，分别用3 个不同式（11）、式（13）、式（14）计算得到的频率归一化绝对误差曲线；而且每个算例3个不同的频率计算公式计算出的结果都用不同的形状表示。图5给出了正弦波信号模型x（t）在直流偏移量B=0，其他信号参数如前述不变情况下，仍在变频率步长0.1Δf情况下对每一个信号分别加该文分析的4种窗函数后，不同截断信号的傅里叶变换频谱函数在零频率处的频谱值变化曲线。5幅图横坐标均为记录样本中所包含的信号周期数（CiR）。

图1 算例1测频误差曲线（步长0.1Δf）

图2 算例2测频误差曲线（步长0.1Δf）

图3 算例3测频误差曲线（步长0.1Δf）

图4 算例1测频误差曲线（步长0.02Δf）

图5 零频率频谱值曲线

4.2 结果与讨论

（1）对照图1～图3可以看出，算例2的3个频率计算公式，算例3的频率计算式（18）、式（20）测频误差太大，大部分频率点测频误差都落在0.4倍的频率分辨率以外，所以这几个校正公式不能使用；算例1的3个频率计算公式以及算例3的频率计算公式（19）均能得到比较好的测频结果。

（2）由图1、图3可以看出，随着采样样本内包含的信号周期个数CiR变大测频误差控制在0.1倍频率分辨率的点越来越少，而且误差比较大的点在图5曲线过零点对应位置成周期出现。原因可从图5得出，如果对信号分别加窗函数1，2，3，4进行FFT变换，对应于同一个CiR，四个离散频谱在零频率点对应频谱值相差不大，就会造成求K时式（8）分母接近零，出现奇点造成计算误差变大。一方面随着采样样本内包含的信号周期个数CiR变大，图5中对应于同一个CiR 4个离散频谱在零频率点对应频谱值逐渐衰减趋于同样大小，从而引起这一奇点效应；另一方面随着图5零频率点对应频谱值的过零点呈周期出现，同样也会引起这一奇点效应，造成计算误差也跟着呈周期变大。可见发生奇点效应是引起这一算法测频精度下降最主要的原因，但由于测频误差不是随周期数（CiR）单调变化，所以适时调节分析点数运用该新算法测频就能够很好地避免这里的奇点效应。

（3）图1、图4虽然是分别用算例1的3个频率计算公式计算出的频率归一化绝对误差，但大部分点是重叠的，原因是上文总结出同一个算例中的3个测频计算公式线性相关，计算结果只有计算机处理数据精度上差别，并无原理上大的不同。

（4）图4在本质上是图1对应研究的局部细化和延伸。可以发现当CiR在区间0.5～2.67时，该文测频新方法误差小于10-4数量级FFT变换分辨率，可以实现频率的高精度测量（完全满足测量电网谐波频率变化的需要[7-9]），在其他CiR大于2.67区间上虽然误差比较大，但可通过减少分析点数将CiR转化至区间 0.5～2.67。

（5）采样密度对精度的影响不显著。采样率首先要满足采样定理的要求，即每个波动周期内至少采到两点。由于固定了采样点数N，所以CiR越高，每个周期内采集的点数越少。但是图1、图3表明采样密度对校正精度的影响不具主导性。

（6）为了更加系统地考察新方法测频的误差特性，重新选取被测正弦波信号模型频率f0从0.1Δf扫描到 10Δf，扫描步长为 0.02Δf，其他信号参数同4.1节开始第一段叙述不变。在变频率情况下考虑初相位角φ0变化时，运用算例1的频率计算公式（11）求出每个频率的180个不同的初相位角情况下频率f0的归一化绝对误差，而后找到其中的最大值，考察这个最大值随CiR变化的趋势，绘制误差曲线包络，如图6所示（a图是CiR在区间0.5～2.67变化时频率误差特性图，b图画出了CiR仅在区间0.5～2.67变化时情况）。该图表明信号初相位角无论如何变化，运用该文分析的测频方法均能得到比较高的精度，再次印证了以上总结出结论的正确性，说明了该文新方法测频的有效性。

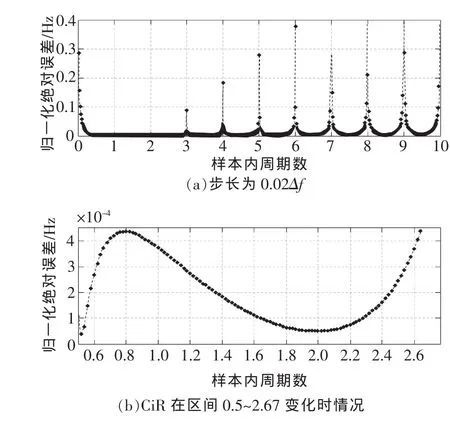
图6 新算法的测频误差包络

5 结束语

普通频谱校正方法由于没有考虑负频谱成分的干涉影响，难以应用于短记录的频谱校正测频中。该文给出了一种基于变窗函数方法的频谱校正的显式测频新方法，采用仿真手段对提出的方法进行了考核。仿真结果表明：

（1）采用窗函数1，2，3进行组合的各类频率计算公式均可以得到比较良好的测频结果，并且不用考虑信号中直流分量的影响。当CiR在区间0.5～2.67时频率误差特别小，在10-4FFT变换分辨率数量级上，并且相位变化和采样密度变化不对测频精度产生较大影响。

（2）影响该新方法测频精度最重要的因素是计算公式中有可能出现奇点。工程应用中应尽量通过选取对应同一频率点频谱差距较大的一组窗函数和调节分析点数，使得采样样本内包含的信号周期个数CiR在对应于测频误差最小的范围内，来很好地回避这一问题。

该文的测频方法只研究了变窗函数对象为矩形窗、Hanning窗、Blanckman窗、Hamming窗情形，其他窗函数情形的测频公式有待进一步发展。此外，在噪声干扰情形下的测频误差的统计特性也有待进一步研究。

[1] 丁 康，谢 明，杨志坚.离散频谱校正理论与技术[M].北京：科学出版社，2007.

[2] 斯托伊卡.现代信号谱分析[M].吴任彪，韩 萍，冯 清，等，译.北京：电子工业出版社，2007.

[3] 陈奎孚，张森文，郭幸福.消除负频率影响的频谱校正[J].机械强度，2004，26（1）：25-28.

[4] 陈奎孚，王建立，张森文.低频成分的频谱校正[J].振动工程学报，2008，21（1）：289-292.

[5] 陈奎孚，王建立，张森文.短记录加汉宁窗的频谱校正[J].振动与冲击，2008，27（4）：49-51.

[6] 段虎明，秦树人，李 宁.离散频谱的校正方法综述[J].振动与冲击，2007，26（11）：138-145.

[7] Radil T，Ramos P M，Serra A C.Frequency estimation of power system signals using a new spectrum leakage correction algorithm[J].IEEE MTC.Victoria，BC，Canada，2008，25（3）：2161-2166.

[8] Radil T，Ramos P M.New spectrum leakage correction algorithm for frequency estimation ofpower system signals [J].IEEE Trans.Instrum.Meas，2008，57（5）：1670-1679.

[9] Agrei D.Power system frequency estimation in the shortened measurement time[C]∥IEEE Instrumentation and Measurement Technology Conference：Budapest，Hungary，2007，21（23）：1094-1098.

[10]王正林，刘 明.精通Matlab7[M].北京：电子工业出版社，2006.