基于多元线性回归分析的风机噪声预测的研究

徐冠基，柏 林，刘小峰，董鹏飞

（重庆大学测试中心，重庆 400030）

1 引 言

能源是国民经济和社会发展的重要战略物资，随着煤、石油等不可再生能源短缺越来越严重，能源问题已成为当今世界瞩目的焦点，各国都在促进可再生能源的发展。风力资源是取之不尽用之不竭的，利用风力发电可以减少环境污染，节省煤炭、石油等常规能源。风力发电技术成熟，在可再生能源中成本相对较低，有着广阔的发展前景。而风力发电机产生的噪声问题作为风力发电场选址过程中的主要矛盾之一，限制了风力发电机在全球范围内大规模布置。因此，对风力发电机进行声发射的测试和评估，对风力发电场的选址具有重要的现实意义[1-3]。

国际电工委员会于1998年制定了“IEC 61400-11，风力发电机组－第11节：声学噪声测量技术”国际标准第一版，以后不断改进，对风力发电机声发射评估过程做出了详细规定，以保证风力发电机声发射评估过程的一致性和结果的可比性[4]。

该文在仔细研究了IEC 61400-11标准后，提出采用多元线性回归分析的方法对风力发电机在开机状态下产生噪声的声压级进行预测，对多元线性回归分析的模型和求解过程进行了建模，求得线性回归方程。

2 多元线性回归分析法

多元线性回归分析是预测分析最常用的方法之一，其基本原理就是：首先对历史数据进行分析，建立数学模型；其次，用最小二乘法求取模型中的未知参数；最后，用回归模型对因变量的变化趋势做出预测。多元线性分析是应用最广泛的统计学分支之一，其主要用途包括用于描述解释现象、用于预测、用于控制等[5]。

2.1 多元线性回归模型的建立[6-7]

多元线性回归分析是研究一个因变y和多个自变量（x1，x2，x3，…，xm）之间线性关系的方法。假设在实际问题中，已经确定了对因变量Y有影响的主要因素有 p-1 个，记为 X1，X2，X3，…，Xp-1，则它们之间可以建立线性回归模型：

式中：β0，β1，β2，…，βp-1——未知参数，称为回归系数；ε——每次观测时的随机误差，满足Gauss-Markov假设，即 ε～N（0，σ2）。

在观测得到n组相互独立的实验数据（xi1，xi2，xi3，…，xip-1）（i=1，2，…，n）后，便可得：

写成矩阵形式为：

其中：

2.2 用最小二乘法求取回归系数[8]

令Q=εTε=（Y-Xβ）T（Y-Xβ），则Q为n次观测误差的平方和，Q应该越小越好，于是可以取使Q取得最小值时的作为系数矩阵β的点估计。

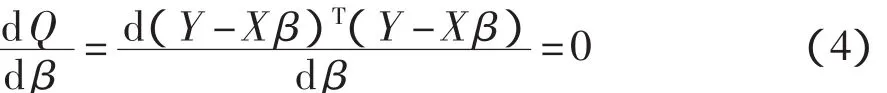
从而得到经验回归方程：

3 多元线性回归分析在风力发电机噪声预测中的应用

3.1 风机声发射评估过程的研究

目前世界各国对风机声发射评估过程的要求，都以IEC的“61400风力发电机系统-第11节：声学噪声测量技术”（简称IEC 61400-11国际标准）中的测量分析方法为主要依据。

为了全面体现风机噪声的特点，标准规定需要对以下参数做出测量：

（1）声学参数。风力发电机组产生的噪声的声压。

（2）非声参数。包括风力发电机组的输出功率、转速、机舱风速、桨距角、偏航角、温度、气压、测风塔风速、风向。

根据标准的规定，必须对风力发电机组产生的噪声的等效连续A计权声压级（简称声压级，用LAeq表示）做出计算。

风力发电机、风电场都有其独特的噪声发生机理：周围环境通常为山村或田园，背景噪声较低，但随风速变化而改变（由气流作用于植物或地表引起），并且具有掩蔽效应。

因此，风机噪声的测试所需仪器设备较多、较杂。如“WINDTEST Kaiser-Wilhelm-KoogGmbH”，该公司在进行某次风机噪声认证时所使用的声压测量仪器、传感器如表1所示。

表1 “WINDTEST Kaiser-Wilhelm-Koog”使用的测量设备

由此可见，在实际测量工作中，声压的测量是不易实现的。因此，可以用多元线性回归分析的方法，通过较易实现的非声学参数的测量近似推断出LAeq。具体过程如图1所示。

图1 多元线性回归分析预测噪声声压级的过程

3.2 建立多元线性回归模型[9]

在对IEC 61400-11国际标准详细研究后，选择了与LAeq有密切关系的几个物理量作为自变量建立数学模型如下：

设：Y 为 LAeq；X1为输出电功率；X2为偏航角；X3为温度；X4为大气压力；X5为转速；X6为桨距角；X7为风向；ε为每次测量时的随机误差。

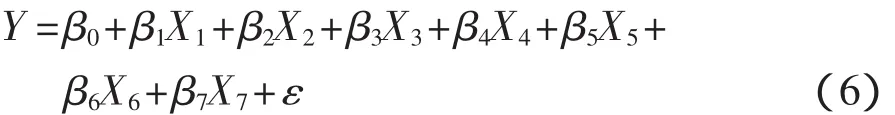
3.3 求取回归系数

2008年5月，在新疆大阪城风场对某公司的1.5MW风力发电机组在开机状态下进行声发射测试，测量得到了噪声的声压、输出电功率、偏航角等上述模型中所需要的各个物理量，并通过计算得到了风机噪声的声压级LAeq。测试持续35min，共得到210组数据。测试完全按照IEC61400-11标准的要求，具有较高的准确性和可信度。通过以上测得的数据，用最小二乘法求解回归系数，得到多元线性回归方程为：

3.4 显著性检验

由于事先并不能确定声压级与上述自变量之间具有线性关系，在建立回归方程之前只是假设它们之间具有确定的线性关系，因而要对所得到的多元线性回归方程进行显著性检验。下面我们运用F检验法，对在3.3中所得到的多元线性回归方程进行显著性检验。

按照假设检验的原理与程序，提出原假设为：

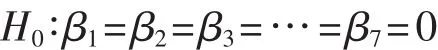
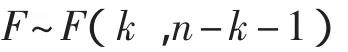
k——变量数，此次检验k=7；

n——样本容量，n=210。

根据变量的样本观测值和估计值计算得到F≈70.99。详细计算结果见表2。

表2 进行显著性检验的结果

给定一个显著性水平α=0.05，查F分布表，得到一个临界值Fα=0.05（7，202）≈1.26。于是有F＞Fα=0.05（7，202），所以线性关系在95%的显著水平下成立。

3.5 计算相对误差

相对误差的计算公式为[10]：

计算得到相对误差的平均值为1.58%，计算结果见图2，误差处于可接受范围内，说明用该多元线性回归模型对风力发电机组噪声的声压级进行预测是有效可行的。

4 结束语

多元线性回归分析经常被用来对某些因变量的变化趋势做出预测。该文给出了风力发电机组声发射测试过程中对风机噪声的声压级进行预测的多元线性回归模型，并于2008年5月在新疆大阪城某风场进行了现场实验。实验结果表明，运用该模型对风力发电机组噪声的声压级进行预测具有较高的精度和很强的实用价值。

图2 相对误差的计算结果

[1]Sun L，Qin SH R，Bo L.Measurement system for wind turbines acoustic noise assessment based on IEC standard and Qin’s model[J].Chinese Journalof Scientific Instruments，2008，29（3）：458-465.

[2] Anon.Turbine noise and the environment[J].Noise Vib Worldwide，2004，35（2）：20-21.

[3]周燕莉.风力发电的现状与发展趋势[J].甘肃科技，2008，24（3）：9-11.

[4]International Electrotechnical Commission.IEC 61400-11：Wind turbine generator systems-Part 11：Acoustic noise measurement techniques Ed.2[S].Switzerland：IEC，2006.

[5] 张尧庭.多元统计分析引论[M].北京：科学出版社，1983.

[6] 张尧庭，朱晓冬.随机向量相关性度量[J].应用概率统计，1988，4（1）：27-34.

[7] 宋来忠，王志明.数学建模与实验[M].北京：科学出版社，2005.

[8] 谢云荪，张志让.数学试验[M].北京：科学出版社，2000.

[9]陈胜利，郭冬琼，张 玥.一种油田产量和可采储量的预测模型及应用[J].承德石油高等专科学校学报，2004（4）：32-35.

[10]秦树人，张明洪，罗德杨.机械工程测试原理与技术[M].重庆：重庆大学出版社，2002.