随钻测量中工具面角的模拟解算
2010-04-26周云凤程为彬陈世琳
周云凤, 程为彬, 陈世琳,2
(1.西安石油大学电子工程学院,陕西 西安 710065;2.青海油田采油三厂,青海 茫崖 816400)
1 引 言
随着石油勘探和开采的精细化要求的提高,对随钻测量仪器的测量精度要求也越来越高[1-2],其中井斜、方位和工具面角等姿态信息直接影响井眼轨迹的测量精度。
利用高精度陀螺仪和三轴加速度计组合测量井眼轨迹[3-5],如果直接将数据送入单片机处理,需要进行A/D转换、采样/保持、多级计算等,这些繁杂过程必然引入各种误差,并且大量的数据运算会使计算机的计算时间增加。由于测量仪器的输出信号与钻具姿态信息存在着一定的三角函数关系[6],可以根据这种函数关系,选用适合的芯片设计模拟电路,来解算出所需的姿态信息,再由单片机做数据处理,以此来简化单片机的计算过程。
2 工具面角解算
2.1 三轴加速度计测量基本原理
在地理坐标系(北西天ONWS坐标系)中建立井下仪器坐标系OXYZ[7-8];设θ和φ分别是井斜角和工具面角,三轴加速度计的各个轴测量的是重力加速度的分量,GX、GY、GZ为三个轴上的输出电压经放大后的值。根据加速度计的测量原理及欧拉定理,可以得出经放大的输出电压与姿态角之间的函数关系。公式如下:

2.2 工具面角计算
由式(1)可知,GX和GY为工具面角φ的函数。则工具面角φ可用GX和GY的比值求反正切后求得:

在实际钻井时,θ与φ可分别取 [0°,180°]和[0°,360°]范围内的任何角度值,所以实际的GX和GY的输出值也可正可负。还需要注意的是,在GX=GY=0时,式(1)并不适用,可结合GZ的输出值判断出,此时井斜角θ的取值为 0°。
反正切算法把对arctgX的求解分解为8个分段函数,简化了计算过程[9]。考虑式(2),设定:
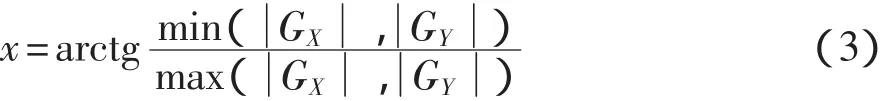
则 x的值必然在[0°,45°]内,这样工具面角 φ 就可以在4个象限中分段表示为关于x的函数,工具面角φ的求解就转化成对x的计算。分段函数表示如下:
式中:I、II、III和IV代表4个象限的序号。
3 模拟解算原理与电路设计
3.1 模拟解算原理
用模拟解算的方式求解钻具姿态,可以避免A/D采样、量化、小值数值运算等误差的引入,同时也能大大简化计算,减少运算时间。工具面角的模拟解算电路原理如图1所示,主要包括放大、取绝对值、比较以及反正切运算等4个部分[10]。
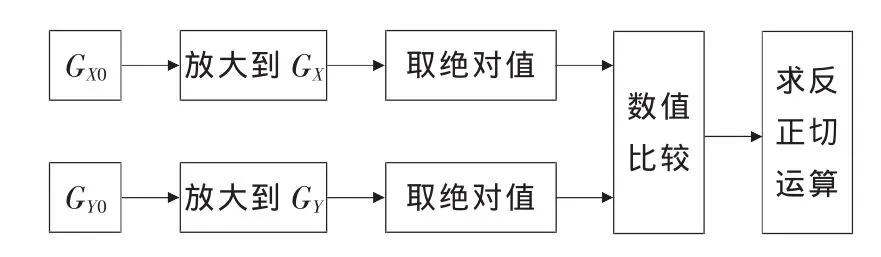
图1 工具面角模拟求解原理框图
图1中GX0、GY0分别是三轴加速度计的X、Y轴上的输出信号,将其最大值的幅值放大到10V,然后各取绝对值并比较大小,将绝对值小者与绝对值大者的比值作为求反正切运算的对象,最后利用模拟函数发生器求解反正切。实现了这样的模拟解算过程,单片机就只需要依照前文对反正切算法的分析,编辑相应程序,根据GX、GY的符号以及两者绝对值的大小判断工具面角φ所在的范围,然后代入模拟函数发生器所求出的反正切值,最终直接求解出φ的实际值。
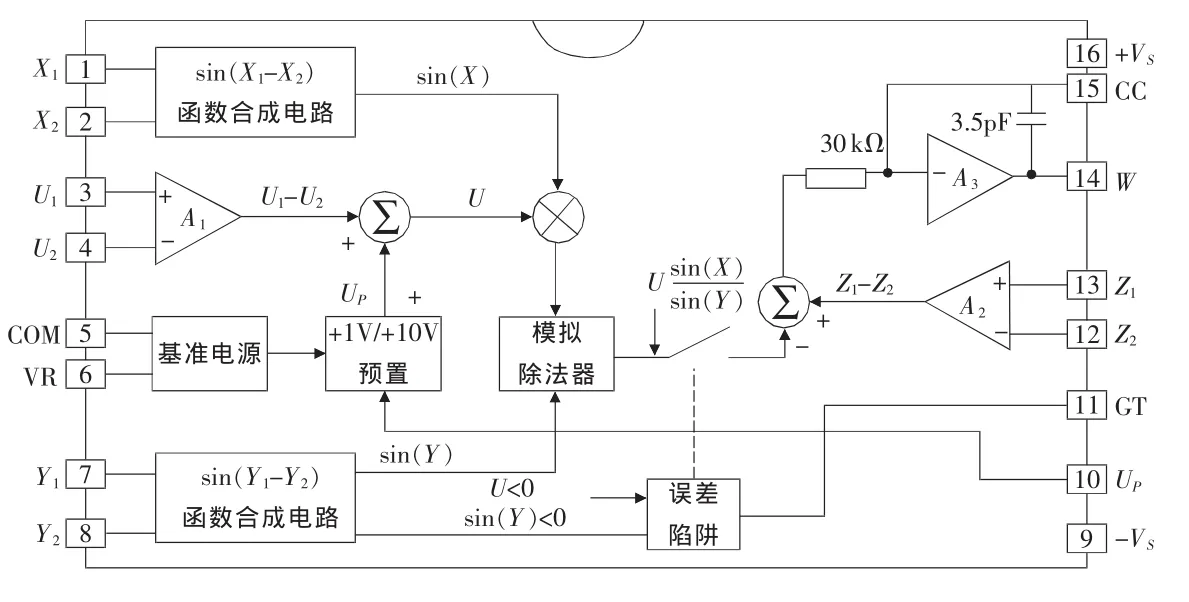
图2 模拟函数发生器原理框图
3.2 反正切求解电路设计
模拟函数发生器可以实现各种标准的三角函数运算,函数之间的转换可通过不同的连接方式来实现,它的一致性比起模拟成形技术要好,总的谐波失真也小很多,速度比用ROM和D/A转换器要快得多。某型号模拟函数发生器的原理如图2所示。根据图2可以得出其输入输出关系为:其中,A为输出放大器A3的开环增益,且U=U1-U2+Up;函数合成电路部分的标度因数选定为50°/V。当开环增益A足够大时,就有:根据式(9),可以通过设定其中各变量的不同取值,实现多种三角函数功能。如果使得Up=0,X1=Z1=U2=0,X2=Y2=VX,Y1=90°,则有:

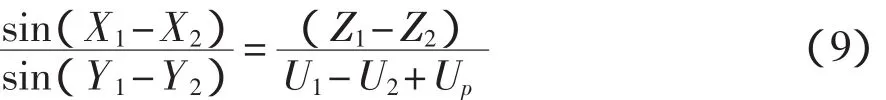

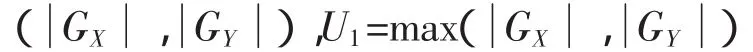
利用模拟函数发生器搭建反正切运算电路,如图3所示。测量中电路的输入由输出电压值可调的集成电路芯片模拟给定。

图3 实验电路原理图
4 实验及数据分析
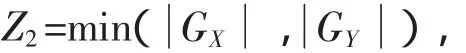
4.1 定井斜实验
当 θ=45°时,取 φ∈[0°,45°],则 U1=GX,Z2=GY,可以计算出理论输入值;将理论输入值取值到小数点后三位作为实际输入值,这样两者会存在一定差距,所以引入根据实际输入值求出的计算值以及计算角度,并作为测量值和测量角度的理论参照。部分实验数据及实验数据曲线如图4和表1所示。
图4(a)的曲线表明当 θ=45°时,利用模拟电路测量得到的工具面角φ的值与理论的计算角度值基本重合,并且电路具有很好的线性度;图4(b)曲线显示最大角度误差不足0.2°,计算得平均误差为0.06°,误差绝对值的数学期望也为0.06°。
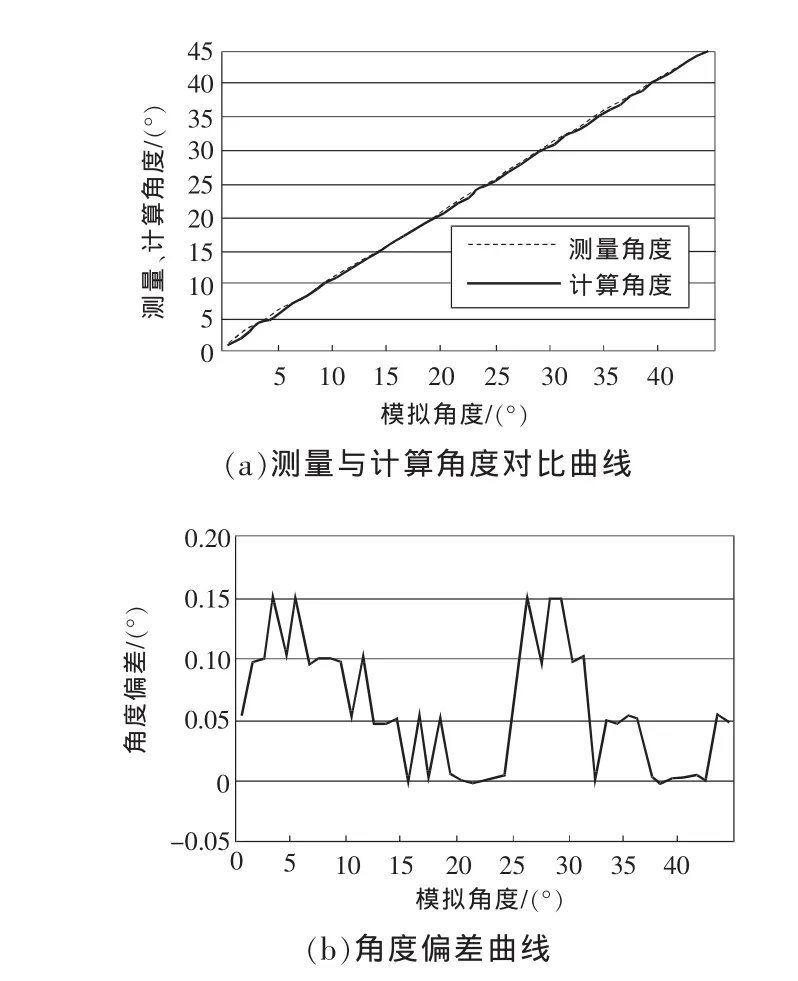
图4 井斜θ=45°时试验数据曲线

表1 θ=45°定井斜实验数据
当 θ=60°时,取 φ∈[0°,45°],方法同上。实验数据及其数值曲线如图5和表2所示。
图5(a)中两条曲线基本重合,说明测量值与理论值很接近,且数值分布具有很好的线性度。图5(b)中,最大角度偏差不足0.2°,计算得平均误差为0.04°,误差绝对值的数学期望为0.07°。
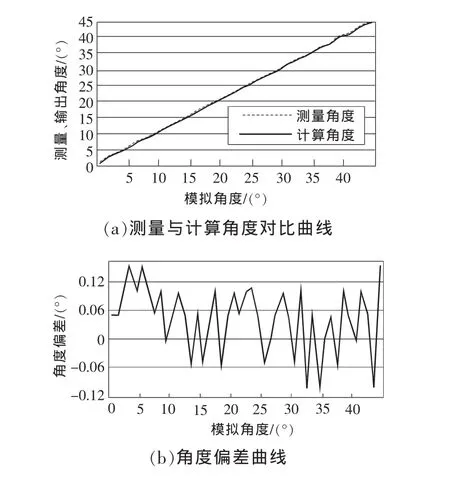
图5 井斜θ=60°时试验数据曲线

表2 θ=60°定井斜实验数据
4.2 变井斜实验
当 θ、φ 同时取[0°,90°]时,两者都小于 45°时,取U1=GX,Z2=GY;两者都大于 45°时,取 U1=GY,Z2=GX。测量方法仍然同上。实验数据及数值曲线如图6和表3所示。
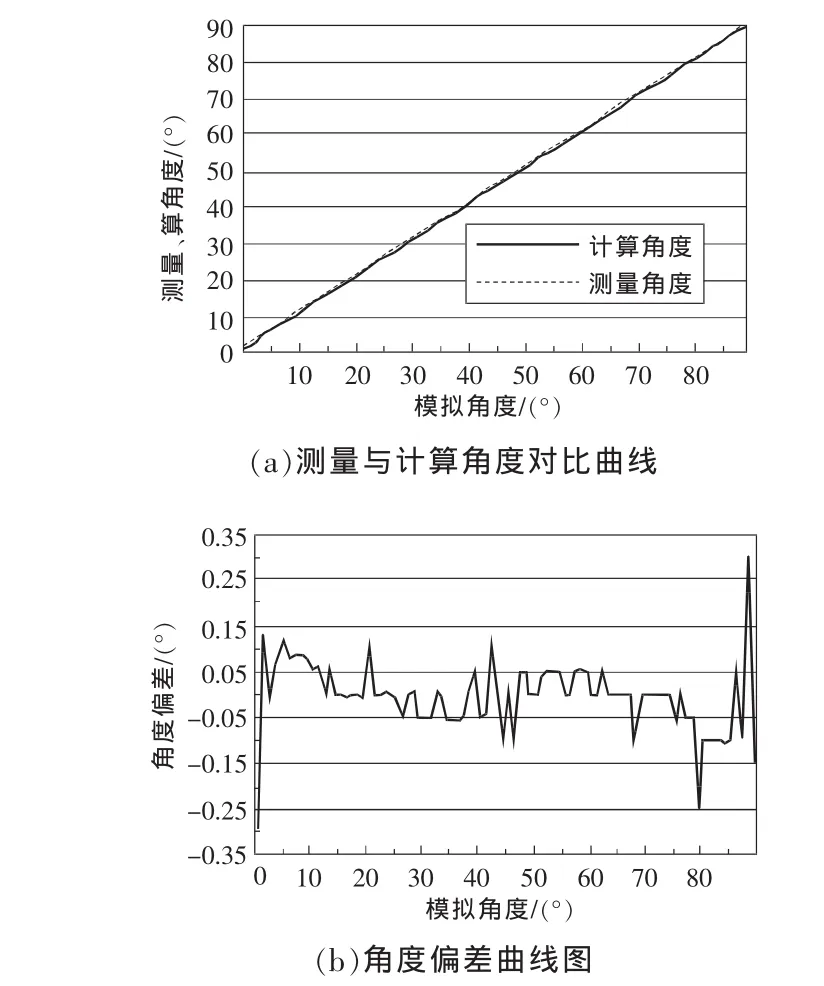
图6 变井斜试验数据曲线
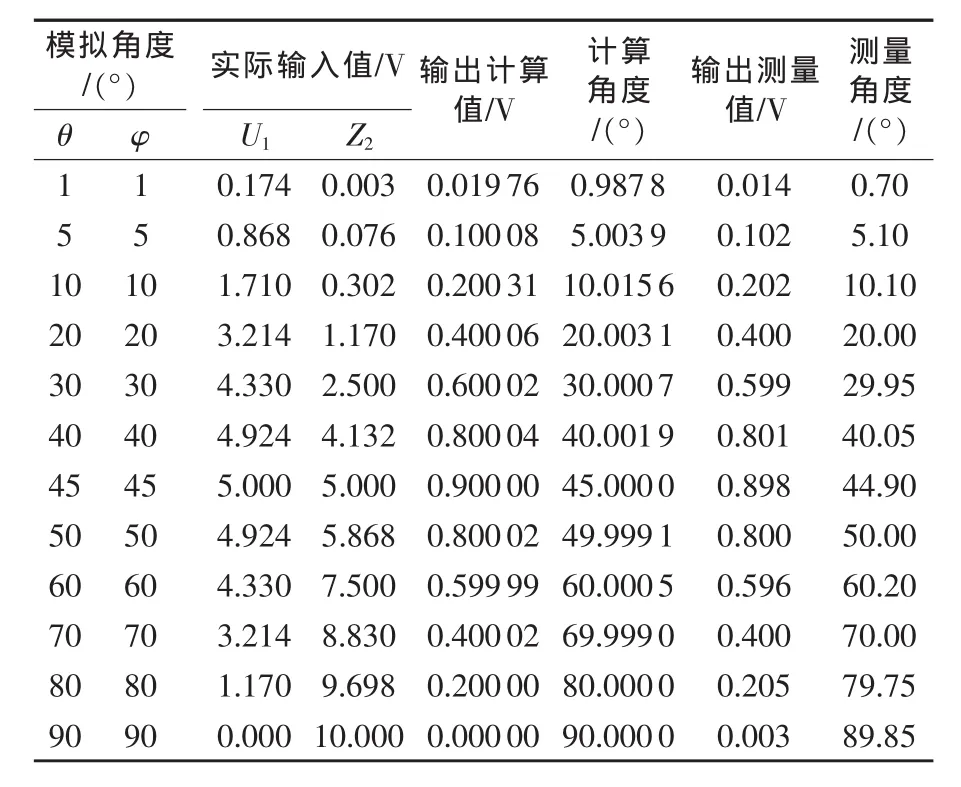
表3 变井斜实验数据
当井斜角和工具面角同时在[0°,90°]取值,测量结果也显示了很好的线性度和很高的精度。图6(b)曲线中的最大误差产生在边界处,这是由于电路不可调零造成的,应将其作为粗大误差处理。则其最大误差为-0.25°,计算得平均误差为-0.004°,误差绝对值的数学期望为0.05°。
实验测量了三种情况下的工具面角,模拟电路的运算功能不受输入值改变的影响,三组测量结果显示,测量角度基本与理论角度重合,最大角度偏差不到0.3°,数值曲线说明电路的线性度及重复性都很好。因此,对实验数据的分析结果表明该电路可以相当准确地实现对钻具姿态中工具面角的模拟解算。
5 结束语
该文提出了一种应用模拟函数发生器实现随钻仪器工具面角计算的新技术,分析了模拟解算的基本原理,设计了模拟解算电路,并进行实验测试,试验数据分析表明工具面角的模拟解算方案可行,电路实现简单,分辨率较高,计算速度快,是一种较好的工具面角解算方法,也可应用到井斜角的模拟解算中。
[1] 石元会,刘志申,葛 华,等.国内随钻测量技术引进及现场应用[J].国外测井技术,2009(1):9-13.
[2] 徐 涛,罗武胜,杜列波,等.水平定向钻进随钻测量及方位校正研究[J].仪器仪表学报,2007,28(2):236-240.
[3] 付鑫生,周 静,汉泽西,等.惯性导航原理在确定井的姿态中的应用[J].测井技术,1992,16(6):451-456.
[4] 周 春,刘白雁,龚 勋.井下实时测斜的理论分析与实验研究[J].中国测试,2009,35(6):1-4.
[5] 狄勤丰,李天太,王文昌.磁独立六加速度计井斜方位角的测量机理研究[J].天然气工业,2005,25(2):67-69.
[6] 陈 琳,程为彬,郭颖娜,等.基于井下姿态测量的余弦函数模拟求解电路设计 [J].电子器件,2009,32(1):104-107,113.
[7] 乐识非.陀螺罗盘定向测量中工具面角计算方法探讨[J].西安石油学院学报:自然科学版,2001,16(4):68-71.
[8] 罗武胜,徐 涛,杜列波.基于加速度计和磁强计的定向钻进姿态测量及方位校正 [J].国防科技大学学报,2007,29(1):106-110.
[9] 郑 勇,汉泽西,付鑫生,等.井姿态参数的工程算法设计[J].西安石油学院学报,1993,8(1):44-49.
[10]陈 琳.垂直钻井工具小角度姿态测量技术研究[D].西安:西安石油大学,2009:50-62.
