标签集中式发布订阅机制性能分析

吴金成，曹 娇，赵文栋，张 磊

(1.解放军理工大学，江苏 南京 210007；2.南京军区通信网络技术管理中心，江苏 南京 210016）

DDS(Data Distribution Service for Real-time Systems)[1]是 OMG(Object Management Group)组织总结发布/订阅系统以往的经验，针对工业过程控制和国防系统应用领域制定的以数据为中心(Data-Centric)的实时数据分发规范。DDS支持基于主题的框架结构实现方式。通过使用虚拟的全球数据空间(Global Data Space,GDS)，实现发布方和订阅方之间的松耦合，使得网络拓扑结构灵活，易于各种网络拓扑结构的实现，如集中式和分布式。DDS可以适应实时性、时效性要求较高的发布订阅需求，并且已经在一些系统中得到应用，如美军的作战系统FCS等[2]。

随着社会各领域信息化程度的提高，大量的信息充斥在信息网络中。对于信息的使用者而言，在大量的数据中获得自己所关心的数据显得尤为重要。DDS发布订阅系统作为一种信息发布的中间件正满足了人类对实时、准确消息传播功能的需要。但由于 DDS规范提出了一个虚拟的GDS的概念，并且所有的数据都经过GDS传播。而GDS只是一个抽象的网络空间，即DDS并没有明确在DDS实现中各参与者(如发布方和订阅方)是如何具体的进行通信交互以及数据匹配的，这就使得不同的DDS实现会使用不同的网络结构并存在不同的性能，也导致了不同DDS实现之间不可互操作。

DDS可以使用的网络结构大体上可以分为集中式和分布式两种。一般的集中式网络结构中，服务器要接收并保存来自数据源的数据信息，充当数据源的代理，为数据需求者提供数据供给服务，因而使得服务器负载过高，易产生热点问题。且在战场的复杂多变的环境下，一旦服务器产生单点失败，将导致所有的发布订阅服务完全中断。分布式的优点在于克服了集中式服务器的单点失败问题，并且降低了出现热点问题的可能性，但在分布式网络结构维护、节点查找等方面的算法实现难度较大，同时存在发布方和订阅方的快速发现、分布式网络的全网时钟同步等问题有待解决。考虑以上两种基本的网络结构的不足，提出使用标签集中式的网络结构。利用发布订阅基本原理，采用标签集中式的网络结构完善参与者之间的交互功能，并对其在军事上普遍使用的无线窄带网络中进行仿真和分析。

1 标签集中式发布订阅系统原理及模型

1.1 标签集中式发布订阅机制原理

所谓标签集中式，既是在集中式架构上加以改进，去掉中心服务器的数据源代理功能，只作为数据源（发布方）和数据需求方（订阅方）供求关系的一个匹配媒介。在匹配成功后，由数据源直接为数据需求方提供数据。具体工作方式为：发布方向服务器注册其所能提供的数据，订阅方向服务器注册其需求；服务器将匹配成功的结果告知订阅方；订阅方根据服务器的反馈，向数据源发布方请求数据；发布方提供数据给订阅方。每一次端到端的通信只有两个应用层的参与者，中心代理服务器不对任何数据进行应用层上的转发。如图1所示。

这种方式的优点在于降低了服务器的负载，并且即使服务器发生单点失败，正在进行的发布订阅服务并不会终止，待服务器恢复后可以继续为新的匹配请求服务，从而提高系统的健壮性。

标签集中式的思想类似于目前互联网应用中的BitTorrent技术。BitTorrent是现有的众多P2P（Peer to Peer）文件共享方法中比较受欢迎的一种。BitTorrent依赖于一个全局的管理系统，以此来保证数据的完整性，同时作为数据代理提供类似目录的功能。已经有相关的文献[3-5]讨论 BitTorrent在有线网中的性能情况。对于标签集中式与发布订阅机制结合并应用于窄带无线网络中的性能情况还没有相应的性能分析和仿真研究。

图1 数据信息分发模式

1.2 网络拓扑

图2 节点分布图

有限区域A内存在N个节点。节点的空间密度定义为单位区域的节点数，记做θ =N/A。为去除边缘节点的特殊性，假设区域A的表面是一个首尾相接的闭合的曲面。这样在进行理论分析时就不存在特殊的节点[6]。虽然对于一些特殊的节点会存在误差，但不会影响仿真结果的总体趋势。且在真正的仿真场景中并没有去特殊化，可以得到更精确的结果。

为简化场景模型，假定所有节点都是均匀的成矩形的分布在区域A中，每一个节点只有四个直接邻居，所谓直接邻居是指刚好一跳可达。对角线上的相邻节点则在通信距离之外。如图2所示。图2中被虚线连接起来的矩形称为级，由中心源节点至远方的各矩形分别为第一级、第二级、第三级等等。

2 标签集中式发布订阅系统数学特征

2.1 前提假设

·每一个节点都随机产生数据消息，数据流满足泊松过程，速率为γ。

·路由平均跳数为 n，即源节点到目的节点的路径长度为n。

·数据包由源到目的节点所需时间为数据包链路传播时间、排队时间和传输时间的和。

·网络链路为低速链路。

·节点的单机处理能力足够强。

·由于信道带宽小，传播时间相对于传输时间足够小，忽略不计。

·节点在产生数据消息的同时，也接收来自其他节点的消息并转发，这些消息都保存在缓存中等待转发。

2.2 通信距离

设节点与其直接邻居之间的距离为两级之间的垂线距离，记做 d。相邻的组成最小矩形的四个节点所覆盖的面积为d2。由区域A的封闭特性得出A=Nd2，即

2.3 路径长度

假设区域A中最大的级数为imax，则一个数据包从源节点出发到达目的地的所经历的路径长度，即跳数，在1至imax之间。所以区域A中路由的平均跳数为

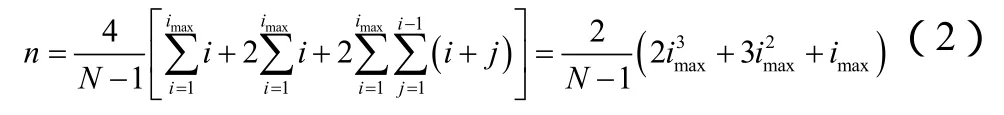
式（2）中第一项和式表示直线路由，第二项和式为矩形对角线路由，第三项和式为其他路由。

2.4 接收端比特错误率

根据上面拓扑图的假设，路由是由相邻节点转发而形成的路径，并且每一跳的距离相同。接收端的信噪比（signal-to-noise ratio,s）决定了链路比特错误率(Bit Error Rate,b)的大小。干扰都是由随机信号组成的，近似于高斯白噪声，此时[7]

假设消息分成多个包传递，每一个包定长 L，在传输时各比特相互独立，那么链路包错误率（packet error rate,p）与比特错误率b的关系为：p =1－（1－b）L。

2.5 重传方式

为了达到可靠传输，当数据包发生错误时需要进行重传。重传的最大次数为K，显然K是一个非常重要的参数。如果K太小，则不能满足QoS的需求。应用程序的不同决定了对数据包错误的容忍程度。用 P表示某应用可以容忍的最大链路数据错误率，即在K次重传之后，p要小于 P。假定各个数据包的传输是相互独立的，那么经过K次重传之后才成功递交数据的可能性是最小的，即K是满足下式的最小值

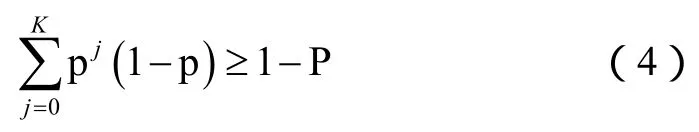
化简得

2.6 移动性

仿真中设定节点随机移动，但是为使通信正常，控制移动距离和速度。在数据进行传输时，节点不应该移动到距离其邻居太远的地方。假设节点最大的移动速度为 V，最大的移动距离为 D =δd，δ ∈ （0,1）。节点应保证在数据包传输的时间t内没有移动出正常的通信范围之外，t =L/v，其中v为节点向网络递交数据包的传输速度。因此t =L/v =D/V，化简得到V =Dv/L。

2.7 标签集中式发布订阅机制服务模型

·数据包成功递交的概率为Ps=（1－p）n。

·数据包的转发时间（包括排队和传输时间）即为其服务时间。数据包作为顾客，节点作为服务员。顾客从进入系统到完成服务，需要按顺序依次经过 c个服务员，且n个节点形成的各个路由组成一个网路，顾客在此网络中排队等待服务。假设每一个服务员的服务时间相互独立，且服从参数为1/µ的负指数分布，则此网络为 Jackson网络。由于每一个节点都会产生数据，即网络存在外部输入，因而此网络为 Jackson开网络。

图3 服务模型示意图

·根据Jackson的结果，平均系统大小应为[8]

则根据Little定理[8]，平均系统时间为

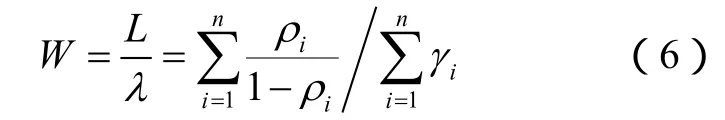
则往返时延RTT =2W。其中λ表示节点总的顾客流量；ρi=λi/µi, i=1,2,…,n。

3 仿真及结果讨论

3.1 仿真平台构建

3.1.1 仿真软件

操作系统：Windows XP SP3

仿真软件：Qualnet 3.7

C编译器：VC++ 6.0

3.1.2 网络协议的选择

应用层：标签集中式发布订阅协议。包长 L为224bits。

传输层：UDP

网络层：IPv4、ICMP、DSR

数据链路层：CSMA

3.1.3 网络环境、电台及物理层参数设置

网络环境：区域A大小为20000*20000m2；节点数量N为9至121个；节点间隔d为2000m；信道频率为300MHz；路径衰减采用自由空间模型；

电台及物理层参数：温度为290K；噪声因子10.0；天线高 1.5m、增益 0dB、有效率 0.8；数据速率为256Kbps；发送功率15dBm；电台通信范围2258.812m，信噪比阈值为10。

其他参数采用默认设置。

3.2 结果及讨论

在理论分析中，由于全网采用集中式架构，节点的数量越多，网络中的流量则越大，网络中心的负载增大，热点问题突出。仿真场景中的网络拓扑结构使得每一个节点在相同方向上的路由选择范围受限，造成网络中心区域部分节点的数据转发量随网络节点数量的增加明显增大，造成一定程度的网络拥塞。因此网络节点数量的增加导致网络数据包往返时延增加以及数据包接收发送比的减小。仿真结果见图4-图7。

图4 数据包接收发送比与节点个数的关系

图4中，随着节点数量的增加数据包接收发送比明显下降，节点数增加至 80时接受发送比下降至50%。这表明网络性能对节点的数量敏感，甚至影响网络的运行。

图5 发布方到服务器往返时延与节点个数的关系

图5中，节点数量增长10倍，发布方到服务器往返时延增长约 10倍。时延随节点数量的增加速度过快，影响网络中时延敏感服务的应用。虽然往返时延总体上成上升趋势，但在81和121个节点处出现往返时延随着节点数量的增加而减小。因为当节点数增加到一定程度时，网络链路的拥塞严重，而且随着节点的增加，路由的平均跳数亦同样随之增加，数据包成功递交的概率Ps减小，使得发布方向服务器注册失败，无法得到往返时延的样本。而在相同情况下，短距离的路由则受此影响较小，数据包依然能够成功递交。从而在发布方到服务器的往返时延的样本空间中由短距离路由得到的样本较多，导致统计曲线成下降趋势。所以图5的统计结果既在趋势上符合理论推导又在测量中符合实际的网络情况。

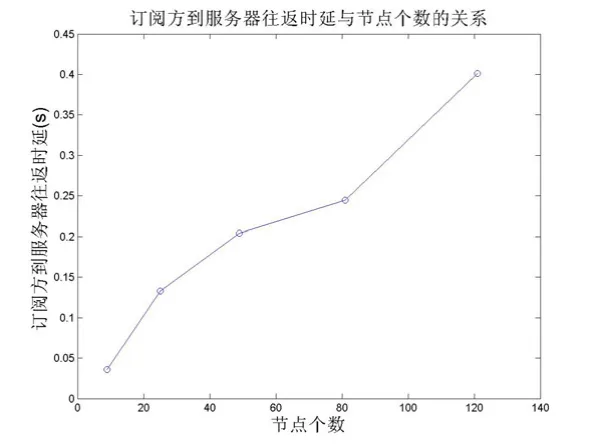
图6 订阅方到服务器往返时延与节点个数的关系

在图6与图5统计的指标相似。但在图6中并没有出现图5中的下降曲线，这主要是因为在协议仿真程序中对不同数据包的不同处理策略造成的。在此网络协议中，对发布方发给服务器的注册信息按需可进行多次确认，确保发布方注册信息在服务器上的准确存储。而对订阅方发给服务器的注册信息只进行一次确认，当订阅方没有收到服务器的确认时会再次的注册。虽然在两种情况下，确认数据包的数量可能相当，但在计算事件发生的次数上却不同。因此导致发布方和订阅方在相同的网络情况下，得出的统计曲线会略有不同。

图7 订阅方到发布方往返时延与节点个数的关系

在图7中可以看到其统计的时延较其他两图中的时延偏大。而图5和图6中的时延大小相当。原因在于，前文中建立的网络拓扑模型由于其环状的封闭性使得以数据源节点为网络中心来阐述问题，但在实际网络仿真拓扑中，只有中心服务器是网络的拓扑中心，因此会产生上面阐述的偏差。同时图7中亦出现下降曲线，与理论结果相悖，原因与图5中所出现的现象相同。

从以上4张仿真图中可以看出，标签集中式的发布订阅服务能较好地适用于无线低速网络，标签集中式发布订阅机制在节点数少于 50的网络中性能能够接受，但当节点数大于50时，不适用于对RTT敏感的服务。节点较多会使网络拥塞，服务器热点现象突出，发布订阅服务性能下降。

4 结束语

本文主要介绍了发布订阅系统的工作机制，并针对标签集中式的数据分发模式进行了较详细的描述。通过建立场景假设，建立数学模型并进行了理论研究。同时对此场景进行仿真验证，分析统计的数据图表，结果表明标签集中式数据分发模式在中小规模的网络中性能较好。

在下一步的工作中可以对仿真协议进行修改优化，重新设定协议中的各种参数。比如在等候对端确认时的定时器值的设定、节点产生数据流的速度等。通过对各参数值的设定，统计出最适用于此种网络环境的参数集，从而提高标签集中式发布订阅系统的性能，扩大其适用范围或者使得某一具体应用在此网络中得到最优性能。

[1]OMG.Data Distribution Service for Real-time Systems v1.2[EB/OL].(2007-01-01) [2007-05-02].http://www.omg.org/.

[2]李小兵.基于发布/订阅机制的传感器数据分发系统的设计与实现[D].南京: 解放军理工大学,2009.

[3]Yao Yue,Chuang Lin,and Zhangxi Tan.Analyzing the performance and fairness of BitTorrent-like networks using a general fluid model[J].Computer Communications,2006,29(18): 3946-3956.

[4]Johan Pouwelse,Pawel Garbacki,Dick Epema,et al.The Bittorrent P2P File-Sharing System: Measurements and Analysis[J].Lecture Notes in Computer Science,2005,3640(1): 205-216.

[5]Lei Guo,Songqing Chen,Zhen Xiao,et al.A performance study of BitTorrent-like peer-to-peer systems[J].IEEE Journal on Selected Areas in Communications,2007,25(1): 155-169.

[6]Sooksan Panichpapiboon,Gianluigi Ferrari,Nawaporn Wisitpongphan,et al.Route Reservation in Ad Hoc Wireless Networks[J].IEEE TRANSACTIONS ON MOBILE COMPUTING,2007,6(1): 56-71.

[7]A.Papoulis,S.U.Pillai.Probability.Random Variables and Stochastic Processes[C].McGraw-Hill,2002.

[8]苏兆龙.排队论基础[M].成都: 成都科技大学出版社,1998.